冀教版初中数学七年级下册 第七章 相交线与平行线复习 教案
文档属性
| 名称 | 冀教版初中数学七年级下册 第七章 相交线与平行线复习 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 45.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:13:21 | ||
图片预览

文档简介
相交线与平行线复习课(第一课时)
【教学目标】1.经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化,
梳理本章的知识结构.
2.通过对知识的梳理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形.
3.使学生认识平面内两条直线的位置关系,
【教学重点与难点】
教学重点:复习平面内两条直线相交的位置关系,以及相交的综合应用.
教学难点:垂直的综合应用.
【教学方法】
通过创设情境,以问题为载体给学生提供探索的空间,引导学生积极探索。教学环节的设计与展开,都以问题的解决为中心,使教学过程成为在教师指导下学生的一种自主探索的学习活动过程,在探索中形成自己的观点。
【教学过程】
一、复习提问
梳理知识
(设计说明:引导学生回忆本章主要内容,形成知识结构图,让学生体会知识之间的内在联系,使学生对知识的认识更加系统化)
在本章相交线中学习了哪些主要内容?
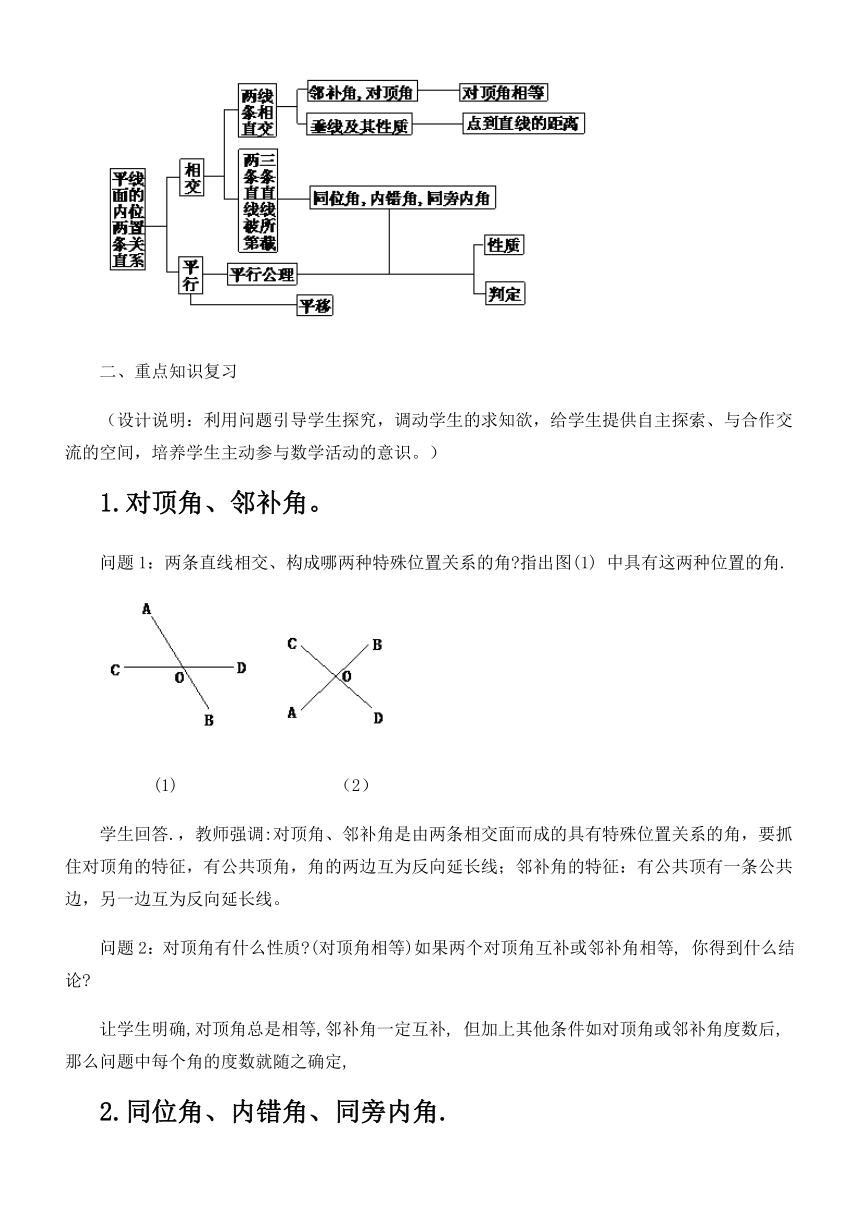
教师根据学生的回答,逐步形成本章的知识结构图:
二、重点知识复习
(设计说明:利用问题引导学生探究,调动学生的求知欲,给学生提供自主探索、与合作交流的空间,培养学生主动参与数学活动的意识。)
1.对顶角、邻补角。
问题1:两条直线相交、构成哪两种特殊位置关系的角?指出图(1)
中具有这两种位置的角.
?
(1)
(2)
学生回答.,教师强调:对顶角、邻补角是由两条相交面而成的具有特殊位置关系的角,要抓住对顶角的特征,有公共顶角,角的两边互为反向延长线;邻补角的特征:有公共顶有一条公共边,另一边互为反向延长线。
问题2:对顶角有什么性质?(对顶角相等)如果两个对顶角互补或邻补角相等,
你得到什么结论?
让学生明确,对顶角总是相等,邻补角一定互补,
但加上其他条件如对顶角或邻补角度数后,那么问题中每个角的度数就随之确定,
2.同位角、内错角、同旁内角.
问题1:如图(3)中,∠1与∠2,∠2与∠3,∠3与∠4分别是什么位置关系的角?
(3)
(4)
只要求学生从图形中找出同位角,内错角,同旁内角.
练习:如图(4),找出∠1、∠2、∠3中哪两个是同位角、内错角、同旁内角.
3.垂线及其性质.
问题1:什么样的两条直线互相垂直?
教师应强调垂线的定义既可以作垂线的判定方法用,也可以作垂线性质用.
作判定用时写成:如图(2),因为∠AOD=90°,所以AB⊥CD,
这是一个角的“数”到两直线垂直的“形”的判断。
作为性质用时写成:如图(2),因为AB⊥CD,所以∠AOD=90°。这是由“形”到“数”的说理。
典型例题:如图(5),直线AB、CD、EF相交于点O,CD⊥EF,∠1=35°,求∠2的度数.
(5)
(6)
(7)
鼓励学生用不同方法求解.
问题2:垂线有哪些性质?
学生叙述垂线的两条性质,懂得分清这两个命题的题设和结论。
学生思考:
①请回忆一下体育课测跳远成绩时,教师是怎样测量的?
②如图(6),AB⊥L,BC⊥L,B为垂足,那么A、B、C三点在同一条直线上吗?为什么?
问题3:什么是点到直线的距离?
学生回答后教师总结:我们已经学习了两种距离,都是距离,就要懂得它们得共同点:距离都是线段的长度,又要懂得区别:两点间的距离是连接这两点的线段的长度,点到直线距离是直线外一点引已知直线的垂线段的长度。
学生练习:①如图(7),四边形ABCD,AD∥BC,AB∥CD,过A作AE⊥BC,过A作AF⊥CD,垂足分别是E、F,量出点A到BC的距离。
三、巩固训练
熟练技能(知识大闯关)
(设计说明:通过形式不同的练习加强学生对知识的理解,训练学生灵活应用知识解决问题的能力)
(一)、判断题.
1.如果两个角是邻补角,那么一个角是锐角,另一个角是钝角.(
)
2.两条直线被第三条直线所截,内错角的对顶角一定相等.(
)
3互为补角的两个角的平行线互相垂直.(
)
4.两条直线都与同一条直线相交,这两条直线必相交.(
)
(二)投影展示1-6题
E
(四)、课下检测卷
D
1、如图1,直线AB、CD相交于点O,∠1=90°:
A
1
B
则∠AOC和∠DOB是
角,∠DOB和∠DOE互为
角,
O
∠DOB和∠BOC互为
角,∠AOC和∠DOE互为
角。
C
图1
2、如图3所示,直线AB、CD相交于点O,作∠DOB=∠DOE,OF平分∠AOE,若
F
E
∠AOC=36°,则∠EOF=
°
D
A
O
B
C
图3
3、下列语句正确的是(
).
A、相等的角是对顶角
B、相等的两个角是邻补角
C、对顶角相等
D、邻补角不一定互补,但可能相等
4、如图2,∠5和∠7是
,∠4和∠6是
,
∠1和∠5是
,∠2与∠6是
,∠1和∠3是
,
∠5和∠6是
。
5.如图(17),是一条河,C河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)
【评价与反思】
全章复习的目的是使学生进一步系统掌握基础知识、基本技能和基本方法,进一步提高综合运用数学知识灵活地分析和解决问题的能力?因此,在选择教学内容时注意了下面两个方面:第一,既加强基础,又提高能力和发展智力;第二,既全面复习,又突出重点。
【教学目标】1.经历对本章所学知识回顾与思考的过程,将本章内容条理化,系统化,
梳理本章的知识结构.
2.通过对知识的梳理,进一步加深对所学概念的理解,进一步熟悉和掌握几何语言,能用语言说明几何图形.
3.使学生认识平面内两条直线的位置关系,
【教学重点与难点】
教学重点:复习平面内两条直线相交的位置关系,以及相交的综合应用.
教学难点:垂直的综合应用.
【教学方法】
通过创设情境,以问题为载体给学生提供探索的空间,引导学生积极探索。教学环节的设计与展开,都以问题的解决为中心,使教学过程成为在教师指导下学生的一种自主探索的学习活动过程,在探索中形成自己的观点。
【教学过程】
一、复习提问
梳理知识
(设计说明:引导学生回忆本章主要内容,形成知识结构图,让学生体会知识之间的内在联系,使学生对知识的认识更加系统化)
在本章相交线中学习了哪些主要内容?
教师根据学生的回答,逐步形成本章的知识结构图:
二、重点知识复习
(设计说明:利用问题引导学生探究,调动学生的求知欲,给学生提供自主探索、与合作交流的空间,培养学生主动参与数学活动的意识。)
1.对顶角、邻补角。
问题1:两条直线相交、构成哪两种特殊位置关系的角?指出图(1)
中具有这两种位置的角.
?
(1)
(2)
学生回答.,教师强调:对顶角、邻补角是由两条相交面而成的具有特殊位置关系的角,要抓住对顶角的特征,有公共顶角,角的两边互为反向延长线;邻补角的特征:有公共顶有一条公共边,另一边互为反向延长线。
问题2:对顶角有什么性质?(对顶角相等)如果两个对顶角互补或邻补角相等,
你得到什么结论?
让学生明确,对顶角总是相等,邻补角一定互补,
但加上其他条件如对顶角或邻补角度数后,那么问题中每个角的度数就随之确定,
2.同位角、内错角、同旁内角.
问题1:如图(3)中,∠1与∠2,∠2与∠3,∠3与∠4分别是什么位置关系的角?
(3)
(4)
只要求学生从图形中找出同位角,内错角,同旁内角.
练习:如图(4),找出∠1、∠2、∠3中哪两个是同位角、内错角、同旁内角.
3.垂线及其性质.
问题1:什么样的两条直线互相垂直?
教师应强调垂线的定义既可以作垂线的判定方法用,也可以作垂线性质用.
作判定用时写成:如图(2),因为∠AOD=90°,所以AB⊥CD,
这是一个角的“数”到两直线垂直的“形”的判断。
作为性质用时写成:如图(2),因为AB⊥CD,所以∠AOD=90°。这是由“形”到“数”的说理。
典型例题:如图(5),直线AB、CD、EF相交于点O,CD⊥EF,∠1=35°,求∠2的度数.
(5)
(6)
(7)
鼓励学生用不同方法求解.
问题2:垂线有哪些性质?
学生叙述垂线的两条性质,懂得分清这两个命题的题设和结论。
学生思考:
①请回忆一下体育课测跳远成绩时,教师是怎样测量的?
②如图(6),AB⊥L,BC⊥L,B为垂足,那么A、B、C三点在同一条直线上吗?为什么?
问题3:什么是点到直线的距离?
学生回答后教师总结:我们已经学习了两种距离,都是距离,就要懂得它们得共同点:距离都是线段的长度,又要懂得区别:两点间的距离是连接这两点的线段的长度,点到直线距离是直线外一点引已知直线的垂线段的长度。
学生练习:①如图(7),四边形ABCD,AD∥BC,AB∥CD,过A作AE⊥BC,过A作AF⊥CD,垂足分别是E、F,量出点A到BC的距离。
三、巩固训练
熟练技能(知识大闯关)
(设计说明:通过形式不同的练习加强学生对知识的理解,训练学生灵活应用知识解决问题的能力)
(一)、判断题.
1.如果两个角是邻补角,那么一个角是锐角,另一个角是钝角.(
)
2.两条直线被第三条直线所截,内错角的对顶角一定相等.(
)
3互为补角的两个角的平行线互相垂直.(
)
4.两条直线都与同一条直线相交,这两条直线必相交.(
)
(二)投影展示1-6题
E
(四)、课下检测卷
D
1、如图1,直线AB、CD相交于点O,∠1=90°:
A
1
B
则∠AOC和∠DOB是
角,∠DOB和∠DOE互为
角,
O
∠DOB和∠BOC互为
角,∠AOC和∠DOE互为
角。
C
图1
2、如图3所示,直线AB、CD相交于点O,作∠DOB=∠DOE,OF平分∠AOE,若
F
E
∠AOC=36°,则∠EOF=
°
D
A
O
B
C
图3
3、下列语句正确的是(
).
A、相等的角是对顶角
B、相等的两个角是邻补角
C、对顶角相等
D、邻补角不一定互补,但可能相等
4、如图2,∠5和∠7是
,∠4和∠6是
,
∠1和∠5是
,∠2与∠6是
,∠1和∠3是
,
∠5和∠6是
。
5.如图(17),是一条河,C河边AB外一点:
(1)过点C要修一条与河平行的绿化带,请作出正确的示意图.
(2)现欲用水管从河边AB,将水引到C处,请在图上测量并计算出水管至少要多少?(本图比例尺为1:2000)
【评价与反思】
全章复习的目的是使学生进一步系统掌握基础知识、基本技能和基本方法,进一步提高综合运用数学知识灵活地分析和解决问题的能力?因此,在选择教学内容时注意了下面两个方面:第一,既加强基础,又提高能力和发展智力;第二,既全面复习,又突出重点。
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
