4.3.1 角 课件(共26张PPT)
图片预览






文档简介
(共26张PPT)
人教版
七上
第四章
几何图形初步
4.3
角
4.3.1
角
教学重点:
角的概念、角度制及角的表示方法.
教学难点:
角的单位换算.
情境引入
时钟的时针与分针
棱锥相交的两条棱
圆规的两只脚
剪刀的两刃交错
2.把观察得到平面图形画在稿纸上,并思考这些图形有什么共同的特征?
1.观察下面图片,你能从中抽象出什么平面图形?
共同特征:
有一个共同的端点和两条射线.
归纳
角的概念:
角的定义:角是由两条具有公共端点的射线组成的.
两条射线的公共端点是这个角的顶点.
两条射线是这个角的两条边.
●
●
角的顶点
角的边
角的边
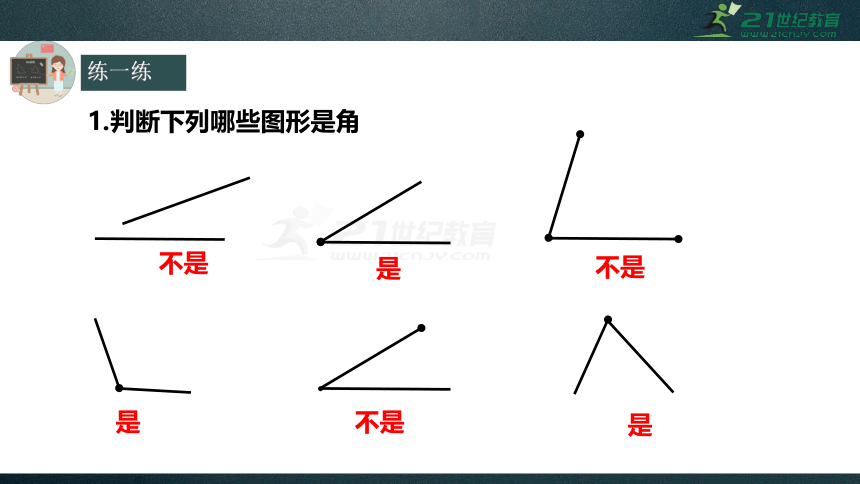
练一练
1.判断下列哪些图形是角
●
●
不是
是
不是
是
不是
是
探究新知
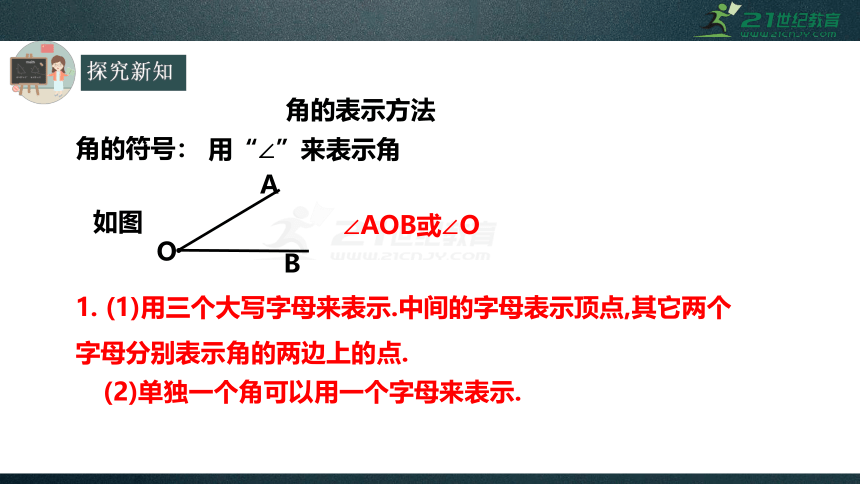
角的表示方法
角的符号:
(2)单独一个角可以用一个字母来表示.
1.
(1)用三个大写字母来表示.中间的字母表示顶点,其它两个字母分别表示角的两边上的点.
用“∠”来表示角
●
A
O
B
如图
∠AOB或∠O
探究新知
2.用一个数字及符号“∠”来表示.在所要表示的角的内部加弧线,在其旁边写上数字.
3.用一个希腊字母及符号“∠”
来表示.用希腊字母来表示角的符号还有β、
γ、
θ,分别读作贝塔、伽玛、西塔.
●
1
如图
用∠1表示
●
α
如图
用∠α表示
读作角“阿尔法”.
方 法
图 形
表 示
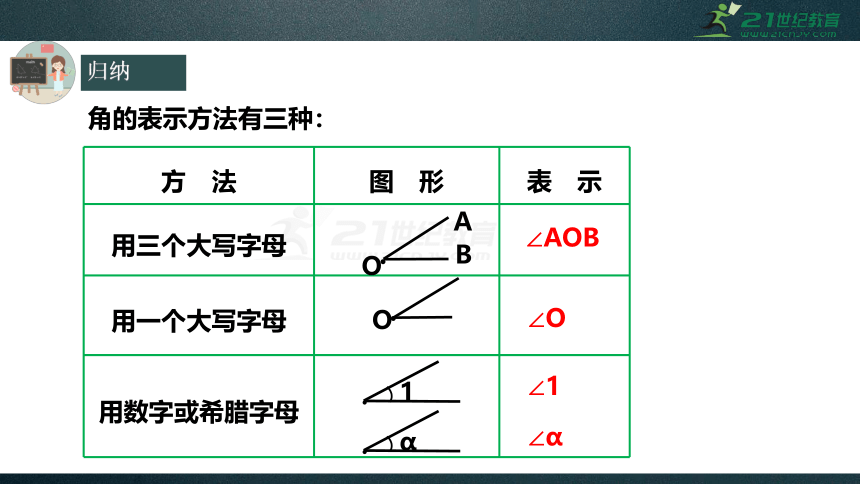
用三个大写字母
用一个大写字母
用数字或希腊字母
归纳
角的表示方法有三种:
●
A
O
B
∠AOB
●
O
∠1
∠O
∠α
●
1
●
α
O
A
如图,角也可以看作由一条射线绕着它的端点旋转而形成的图形.
探究新知
A
O
B
射线OA绕点O旋转,当终止位置
OB和起始位置OA
成一条直线时,形成什么角?
继续旋转,OB
和OA
重合时,又形成什么角?
B
O
A
平角
周角
练一练
1.下列说法正确的是(
).
A
一个周角就是一条射线
B
平角是一条直线
C
角也可以看作由一条射线绕着它的端点旋转而形成的图形.
D
有公共点的两条射线组成的图形叫作角
C
探究新知
2.下列图中能用∠AOB,∠O,∠1三种方法表示同一个角的图形是(
).
D
探究新知
量角器
我们常用量角器量角,度、分、秒是常用的角的度量单位.
把一个周角
360
等分,每一份就是1度的角,记作1°.
1°
把1度的角
60等分,每一份叫做1分的角,记作1’.
把1分的角
60等分,每一份叫做1秒的角,记作1″.
例如,∠α的度数是48度56分37秒,记作∠α=48°56'37".
探究新知
1周角=
,平角=
,直角=
.
180°
360°
1°=
,
1′
=
,
60′
60″
角的度、分、秒是60进制的,这和计量时间的时、分、秒是一样的.以度、分、秒为单位的角的度量制,叫做角度制.
90°
角度制起源于四大文明古国之一的古代巴比伦.为什么选择
60这个数作为进制的基数呢?
据说是由于60这个数是许多常用的数
2,3,4,5,6,10,12,15,20,30的倍数,60=12×5,12是一年中的月数,5是一只手的手指数,所以古代巴比伦人认为60是一个特别而又重要的数.
主题小标
你们想还有其他度量角的单位制吗?
例如,我们以后将要学到的以弧度为基本度量单位的弧度制,在军事上经常使用的角的密位制等.
借助三角尺,我们可以画出
30°,45°,60°,
90°等特殊角,借助量角器,可以画出任何给定度数(如
36°,108°)的角.
探究新知
例
(1)用度、分、秒表示28.36°;
(2)用度表示25°16'48″
.
分析:度、分、秒换算关系:
1°=60′
,
1′=60″
,反过来
解:(1)28.36°=28°+0.36×
60′
=28°+21.6′
=28°21′+0.6×60″
=28°21′36″
探究新知
(2)根据1°=60′,1'=60",得
48″
÷60=0.8,
16.8'
÷60=0.28°
所以25°16'48″
=25.28°.
归纳
2.小单位化成大单位用除法,需要除以进率,先将最小的单位向它的上一级单位换算,逐步进行,直到化成最大的单位度.
1.大单位化小单位用乘法,需要乘进率,先把度化成分,如果还有小数再化成秒.
课堂练习
1.下列说法正确的是(
).
A
直线是一个角.
B
在∠ABC一边的延长线上取一点D.
C
∠AOC
的边是射线
OA,OC.
D
有公共点的两条射线组成的图形叫作角.
C
课堂练习
2.能用两种方法表示同一个角的是(
).
A
∠1和∠A
B
∠2和∠C
C
∠3和∠C
D
∠2和∠B
3.在上午8点整时,时钟的时针与分针之间的夹角(小于平角)是(
).
A
60°
B
90°
C
120°
D.150°
C
D
课堂练习
4.某电视节目在9:10
准时开播,此时时钟上的分针与时针所成的小于平角的角是多少度?
答:9:10
时分针与时针的夹角为
145°.
所以10×6°=60°,
9:10时夹角为
90°+60°—5°=145°.
解:因为时针每分钟旋转
0.5°,
所以10×0.5°=5°,
因为分针每分钟旋转6°,
9:00
时分针与时针的夹角为
90°,
∠A即是
,
∠B即是
,
∠3即是
,
∠β即是
,
∠γ即是
.
课堂练习
5.如图,根据要求填空∶
(1)图中有
个小于平角的角.
(2)分别填出下列各角的另一种表示方法∶
2
1
A
E
B
γ
3
β
C
D
7
∠1
∠2
∠CEB
∠CED
∠AEB
课堂练习
6.
(1)用度、分、秒表示15.27°;
(2)用度表示37°24′18″
.
解:(1)15.27°=15°+0.27×
60′
=15°+16.2′
=15°16′+0.2×60″
=15°16′12″
课堂练习
(2)用度表示37°24′18″
解:(2)根据1°=60′,1'=60",得
18″
÷60=0.3,
24.3'
÷60=0.405°
所以37°24′18″
=37.405°.
课堂小结
1.角的静态和动态的两种定义.
2.角的表示方法.
3.角度制的概念.
4.角的度量单位及换算.
课外作业
第134页第1、2题
https://www.21cnjy.com/help/help_extract.php
人教版
七上
第四章
几何图形初步
4.3
角
4.3.1
角
教学重点:
角的概念、角度制及角的表示方法.
教学难点:
角的单位换算.
情境引入
时钟的时针与分针
棱锥相交的两条棱
圆规的两只脚
剪刀的两刃交错
2.把观察得到平面图形画在稿纸上,并思考这些图形有什么共同的特征?
1.观察下面图片,你能从中抽象出什么平面图形?
共同特征:
有一个共同的端点和两条射线.
归纳
角的概念:
角的定义:角是由两条具有公共端点的射线组成的.
两条射线的公共端点是这个角的顶点.
两条射线是这个角的两条边.
●
●
角的顶点
角的边
角的边
练一练
1.判断下列哪些图形是角
●
●
不是
是
不是
是
不是
是
探究新知
角的表示方法
角的符号:
(2)单独一个角可以用一个字母来表示.
1.
(1)用三个大写字母来表示.中间的字母表示顶点,其它两个字母分别表示角的两边上的点.
用“∠”来表示角
●
A
O
B
如图
∠AOB或∠O
探究新知
2.用一个数字及符号“∠”来表示.在所要表示的角的内部加弧线,在其旁边写上数字.
3.用一个希腊字母及符号“∠”
来表示.用希腊字母来表示角的符号还有β、
γ、
θ,分别读作贝塔、伽玛、西塔.
●
1
如图
用∠1表示
●
α
如图
用∠α表示
读作角“阿尔法”.
方 法
图 形
表 示
用三个大写字母
用一个大写字母
用数字或希腊字母
归纳
角的表示方法有三种:
●
A
O
B
∠AOB
●
O
∠1
∠O
∠α
●
1
●
α
O
A
如图,角也可以看作由一条射线绕着它的端点旋转而形成的图形.
探究新知
A
O
B
射线OA绕点O旋转,当终止位置
OB和起始位置OA
成一条直线时,形成什么角?
继续旋转,OB
和OA
重合时,又形成什么角?
B
O
A
平角
周角
练一练
1.下列说法正确的是(
).
A
一个周角就是一条射线
B
平角是一条直线
C
角也可以看作由一条射线绕着它的端点旋转而形成的图形.
D
有公共点的两条射线组成的图形叫作角
C
探究新知
2.下列图中能用∠AOB,∠O,∠1三种方法表示同一个角的图形是(
).
D
探究新知
量角器
我们常用量角器量角,度、分、秒是常用的角的度量单位.
把一个周角
360
等分,每一份就是1度的角,记作1°.
1°
把1度的角
60等分,每一份叫做1分的角,记作1’.
把1分的角
60等分,每一份叫做1秒的角,记作1″.
例如,∠α的度数是48度56分37秒,记作∠α=48°56'37".
探究新知
1周角=
,平角=
,直角=
.
180°
360°
1°=
,
1′
=
,
60′
60″
角的度、分、秒是60进制的,这和计量时间的时、分、秒是一样的.以度、分、秒为单位的角的度量制,叫做角度制.
90°
角度制起源于四大文明古国之一的古代巴比伦.为什么选择
60这个数作为进制的基数呢?
据说是由于60这个数是许多常用的数
2,3,4,5,6,10,12,15,20,30的倍数,60=12×5,12是一年中的月数,5是一只手的手指数,所以古代巴比伦人认为60是一个特别而又重要的数.
主题小标
你们想还有其他度量角的单位制吗?
例如,我们以后将要学到的以弧度为基本度量单位的弧度制,在军事上经常使用的角的密位制等.
借助三角尺,我们可以画出
30°,45°,60°,
90°等特殊角,借助量角器,可以画出任何给定度数(如
36°,108°)的角.
探究新知
例
(1)用度、分、秒表示28.36°;
(2)用度表示25°16'48″
.
分析:度、分、秒换算关系:
1°=60′
,
1′=60″
,反过来
解:(1)28.36°=28°+0.36×
60′
=28°+21.6′
=28°21′+0.6×60″
=28°21′36″
探究新知
(2)根据1°=60′,1'=60",得
48″
÷60=0.8,
16.8'
÷60=0.28°
所以25°16'48″
=25.28°.
归纳
2.小单位化成大单位用除法,需要除以进率,先将最小的单位向它的上一级单位换算,逐步进行,直到化成最大的单位度.
1.大单位化小单位用乘法,需要乘进率,先把度化成分,如果还有小数再化成秒.
课堂练习
1.下列说法正确的是(
).
A
直线是一个角.
B
在∠ABC一边的延长线上取一点D.
C
∠AOC
的边是射线
OA,OC.
D
有公共点的两条射线组成的图形叫作角.
C
课堂练习
2.能用两种方法表示同一个角的是(
).
A
∠1和∠A
B
∠2和∠C
C
∠3和∠C
D
∠2和∠B
3.在上午8点整时,时钟的时针与分针之间的夹角(小于平角)是(
).
A
60°
B
90°
C
120°
D.150°
C
D
课堂练习
4.某电视节目在9:10
准时开播,此时时钟上的分针与时针所成的小于平角的角是多少度?
答:9:10
时分针与时针的夹角为
145°.
所以10×6°=60°,
9:10时夹角为
90°+60°—5°=145°.
解:因为时针每分钟旋转
0.5°,
所以10×0.5°=5°,
因为分针每分钟旋转6°,
9:00
时分针与时针的夹角为
90°,
∠A即是
,
∠B即是
,
∠3即是
,
∠β即是
,
∠γ即是
.
课堂练习
5.如图,根据要求填空∶
(1)图中有
个小于平角的角.
(2)分别填出下列各角的另一种表示方法∶
2
1
A
E
B
γ
3
β
C
D
7
∠1
∠2
∠CEB
∠CED
∠AEB
课堂练习
6.
(1)用度、分、秒表示15.27°;
(2)用度表示37°24′18″
.
解:(1)15.27°=15°+0.27×
60′
=15°+16.2′
=15°16′+0.2×60″
=15°16′12″
课堂练习
(2)用度表示37°24′18″
解:(2)根据1°=60′,1'=60",得
18″
÷60=0.3,
24.3'
÷60=0.405°
所以37°24′18″
=37.405°.
课堂小结
1.角的静态和动态的两种定义.
2.角的表示方法.
3.角度制的概念.
4.角的度量单位及换算.
课外作业
第134页第1、2题
https://www.21cnjy.com/help/help_extract.php
