人教版数学八年级上册 12.2三角形全等的判定同步测试题(一) (word版 含解析)
文档属性
| 名称 | 人教版数学八年级上册 12.2三角形全等的判定同步测试题(一) (word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 20:32:30 | ||
图片预览


文档简介
三角形全等的判定同步测试题(一)
一.选择题
1.如图,已知点B、E、C、F在同一直线上,且BE=CF,∠ABC=∠DEF,那么添加一个条件后.仍无法判定△ABC≌△DEF的是( )
A.AC=DF
B.AB=DE
C.AC∥DF
D.∠A=∠D
2.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充条件后,能直接应用“SAS”判定△ABC≌△DEF的是( )
A.∠A=∠D
B.∠ACB=∠DEF
C.AC=DF
D.BF=EC
3.如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )
A.110°
B.125°
C.130°
D.155°
4.如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS
B.SAS
C.SSA
D.ASA
5.如图,点B、F、C、E在一条直线上,AB∥DE,AC∥DF,那么添加下列一个条件后,仍无法判断△ABC≌△DEF的是( )
A.AB=DE
B.∠A=∠D
C.AC=DF
D.BF=EC
6.下列判定直角三角形全等的方法,不正确的是( )
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一直角边对应相等
D.两个直角三角形的面积相等
7.要测量河岸相对两点A、B的距离,已知AB垂直于河岸BF,先在BF上取两点C、D,使CD=CB,再过点D作BF的垂线段DE,使点A、C、E在一条直线上,如图,测出BD=10,ED=5,则AB的长是( )
A.2.5
B.10
C.5
D.以上都不对
8.下列叙述中:
①任意一个三角形的三条高至少有一条在此三角形内部;
②以a,b,c为边(a,b,c都大于0,且a+b>c)可以构成一个三角形;
③一个三角形内角之比为3:2:1,此三角形为直角三角形;
④有两个角和一条边对应相等的两个三角形全等;
正确的有( )个.
A.1
B.2
C.3
D.4
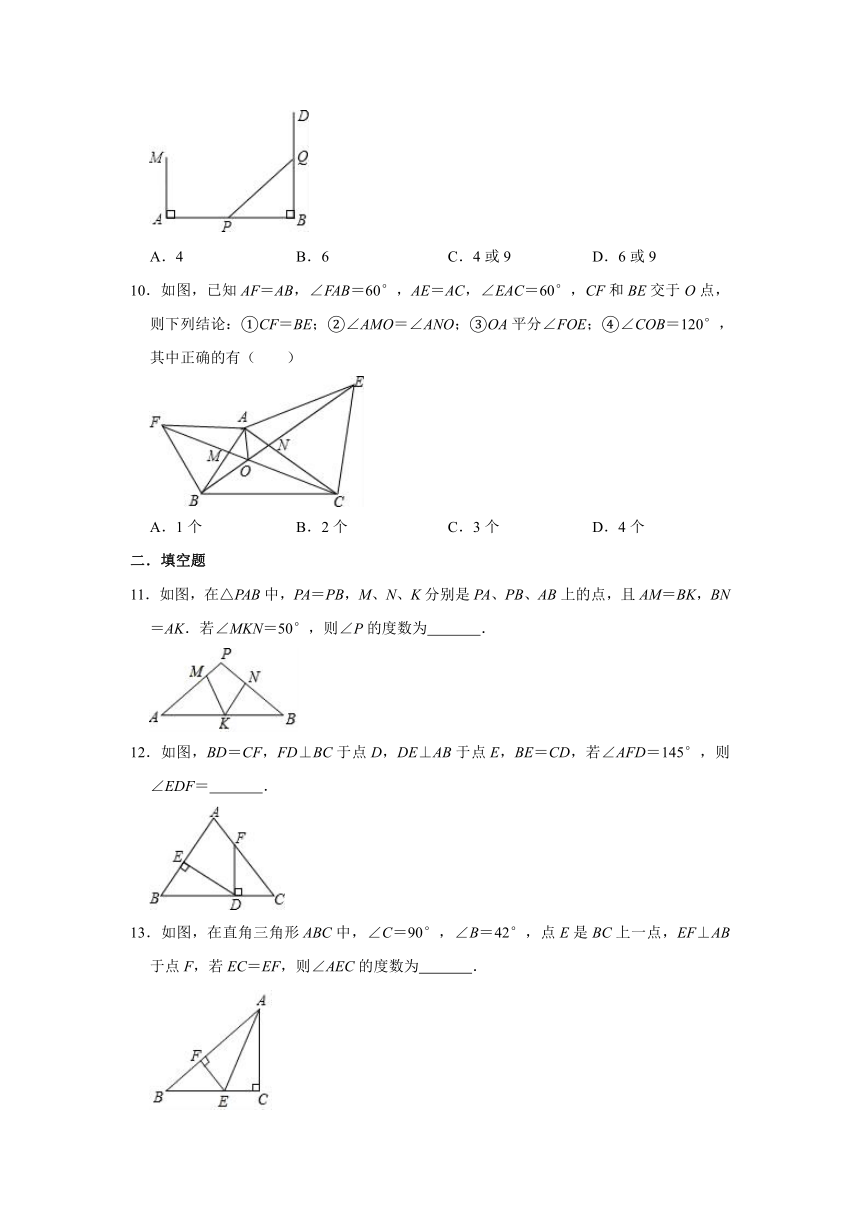
9.如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走2米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.4
B.6
C.4或9
D.6或9
10.如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠AMO=∠ANO;③OA平分∠FOE;④∠COB=120°,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
二.填空题
11.如图,在△PAB中,PA=PB,M、N、K分别是PA、PB、AB上的点,且AM=BK,BN=AK.若∠MKN=50°,则∠P的度数为
.
12.如图,BD=CF,FD⊥BC于点D,DE⊥AB于点E,BE=CD,若∠AFD=145°,则∠EDF=
.
13.如图,在直角三角形ABC中,∠C=90°,∠B=42°,点E是BC上一点,EF⊥AB于点F,若EC=EF,则∠AEC的度数为
.
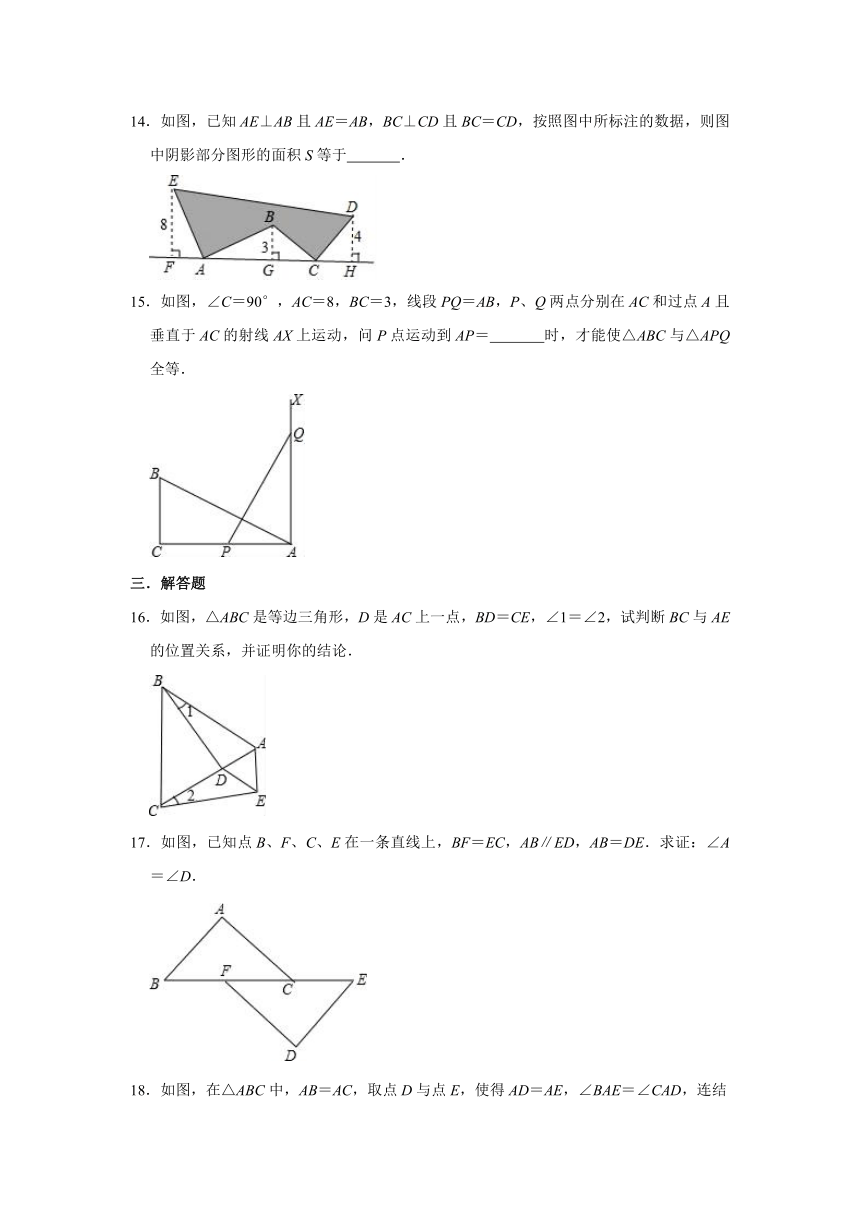
14.如图,已知AE⊥AB且AE=AB,BC⊥CD且BC=CD,按照图中所标注的数据,则图中阴影部分图形的面积S等于
.
15.如图,∠C=90°,AC=8,BC=3,线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=
时,才能使△ABC与△APQ全等.
三.解答题
16.如图,△ABC是等边三角形,D是AC上一点,BD=CE,∠1=∠2,试判断BC与AE的位置关系,并证明你的结论.
17.如图,已知点B、F、C、E在一条直线上,BF=EC,AB∥ED,AB=DE.求证:∠A=∠D.
18.如图,在△ABC中,AB=AC,取点D与点E,使得AD=AE,∠BAE=∠CAD,连结BD与CE交于点O.求证:
(1)△ABD≌△ACE;
(2)OB=OC.
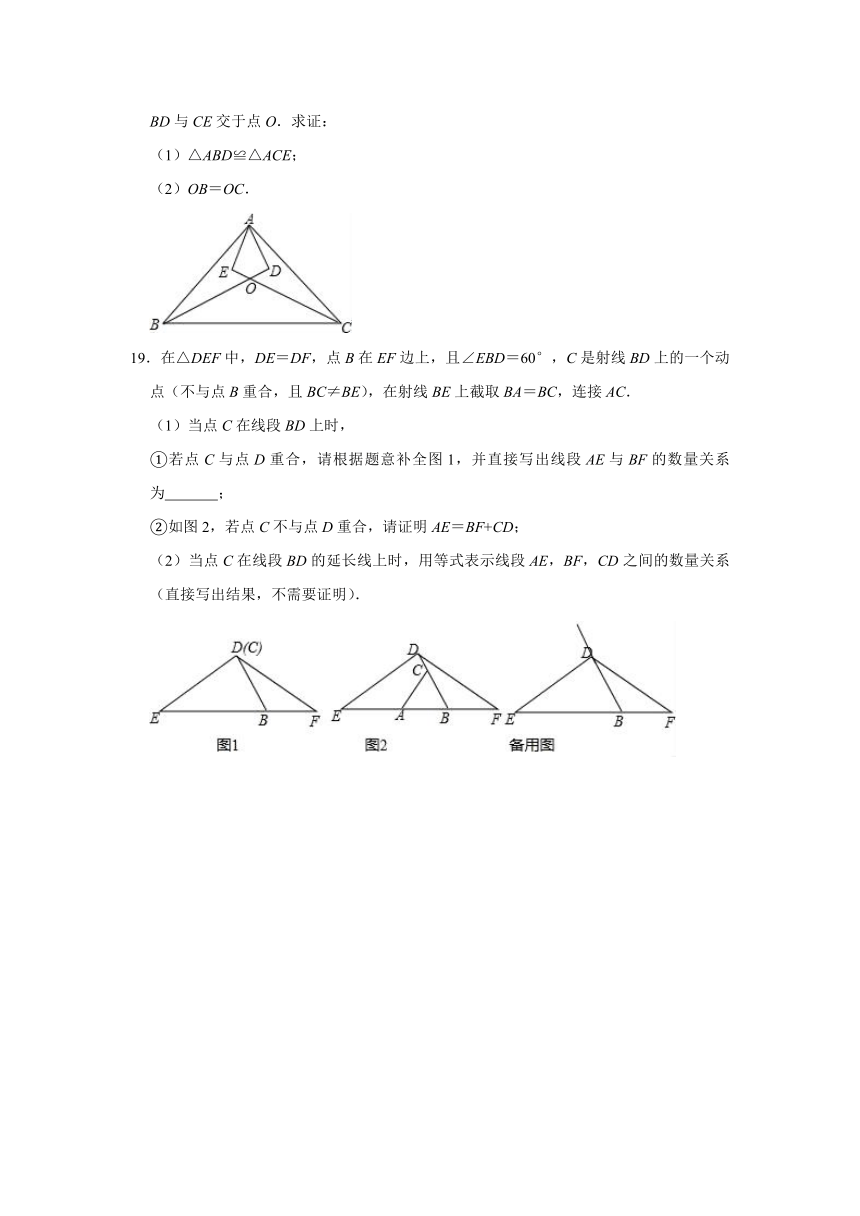
19.在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为
;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE,BF,CD之间的数量关系(直接写出结果,不需要证明).
参考答案与试题解析
一.选择题
1.【解答】解:
∵BE=CF,
∴BE+EC=EC+CF,即BC=EF,且∠ABC=∠DEF,
∴当AC=DF时,满足SSA,无法判定△ABC≌△DEF,故A不能;
当AB=DE时,满足SAS,可以判定△ABC≌△DEF,故B可以;
当AC∥DF时,可得∠ACB=∠F,满足ASA,可以判定△ABC≌△DEF,故C可以;
当∠A=∠D时,满足AAS,可以判定△ABC≌△DEF,故D可以;
故选:A.
2.【解答】解:补充BF=EC,理由如下:
∵BF=EC,
∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF(SAS),
故选:D.
3.【解答】解:
在△ACD和△BCE中
∴△ACD≌△BCE(SSS),
∴∠ACD=∠BCE,∠A=∠B,
∴∠BCA+∠ACE=∠ACE+∠ECD,
∴∠ACB=∠ECD=(∠BCD﹣∠ACE)=×(155°﹣55°)=50°,
∵∠B+∠ACB=∠A+∠APB,
∴∠APB=∠ACB=50°,
∴∠BPD=180°﹣50°=130°,
故选:C.
4.【解答】解:由图可知,三角形两角及夹边可以作出,
所以,依据是ASA.
故选:D.
5.【解答】解:∵AB∥DE,AC∥DF,
∴∠B=∠E,∠ACB=∠DFE,
A、添加AB=DE可利用AAS判断△ABC≌△DEF,故此选项不合题意;
B、添加∠A=∠D无法判断△ABC≌△DEF,故此选项符合题意;
C、添加AC=DF可利用AAS判断△ABC≌△DEF,故此选项不合题意;
D、添加BF=EC可得BC=EF,可利用ASA判断△ABC≌△DEF,故此选项不合题意;
故选:B.
6.【解答】解:如果在两个直角三角形中,两条直角边对应相等,
那么根据SAS即可判断两三角形全等,故选项A正确;
如果如果在两个直角三角形中,斜边和一锐角对应相等,
那么根据AAS可判断两三角形全等,故选项B正确;
如果如果在两个直角三角形中,斜边和一直角边对应相等,
那么根据HL可判断两三角形全等,故选项C正确;
如果两个直角三角形的面积相等,那么无法判定两个直角三角形全等,故D错误;
故选:D.
7.【解答】解:∵AB⊥BD,ED⊥AB,
∴∠ABC=∠EDC=90°,
在△ABC和△EDC中,,
∴△ABC≌△EDC(ASA),
∴AB=ED=5.
故选:C.
8.【解答】解:∵锐角三角形的三条高都在三角形的内部,直角三角形有一条高在三角形的内部,两条在三角形的两边上,钝角三角形的一条高在三角形的内部,两条高在三角形的外部,∴①正确;
∵当a=2,b=c=1时,满足a+b>c,但是边长为1、1、2不能组成三角形,∴②错误;
∵设三角形的三角为3x°,2x°,x°,
∴由三角形的内角和定理得:3x+2x+x=180,
∴x=30,
3x=90,即三角形是直角三角形,∴③正确;
∵有两个角和一条边对应相等的两个三角形全等,∴④正确;
故选:C.
9.【解答】解:当△APC≌△BQP时,AP=BQ,即18﹣x=2x,
解得:x=6;
当△APC≌△BPQ时,AP=BP=AB=9米,
此时所用时间为9秒,AC=BQ=18米,不合题意,舍去;
综上,出发6秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
故选:B.
10.【解答】解:∵△ABF和△ACE是等边三角形,
∴AB=AF,AC=AE,∠FAB=∠EAC=60°,
∴∠FAB+∠BAC=∠EAC+∠BAC,
即∠FAC=∠BAE,
在△ABE与△AFC中,
,
∴△ABE≌△AFC(SAS),
∴BE=FC,故①正确,∠AEB=∠ACF,
∵∠EAN+∠ANE+∠AEB=180°,∠CON+∠CNO+∠ACF=180°,∠ANE=∠CNO
∴∠CON=∠CAE=60°=∠MOB,
∴∠BOC=180°﹣∠CON=120°,故④正确,
连AO,过A分别作AP⊥CF与P,AM⊥BE于Q,如图,
∵△ABE≌△AFC,
∴S△ABE=S△AFC,
∴CFAP=BEAQ,而CF=BE,
∴AP=AQ,
∴OA平分∠FOE,所以③正确,
∵∠AMO=∠MOB+∠ABE=60°+∠ABE,∠ANO=∠CON+∠ACF=60°+∠ACF,
显然∠ABE与∠ACF不一定相等,
∴∠AMO与∠ANO不一定相等,故②错误,
综上所述正确的有:①③④.
故选:C.
二.填空题(共5小题)
11.【解答】解:∵PA=PB,
∴∠A=∠B,
在△MAK和△KBN中,
,
∴△MAK≌△KBN(SAS),
∴∠AMK=∠BKN,
∵∠BKM=∠A+∠AMK=∠MKN+∠BKN,
∴∠A=∠MKN=50°,
∴∠A=∠B=50°,
∴∠P=180°﹣2×50°=80°.
故答案为80°.
12.【解答】解:∵FD⊥BC于点D,DE⊥AB于点E,
∴∠BED=∠FDC=90°,
∵BE=CD,BD=CF,
∴Rt△BED≌Rt△CDF(HL),
∴∠BDE=∠CFD,
∵∠AFD=145°,
∴∠DFC=35°,
∴∠BDE=35°,
∴∠EDF=90°﹣35°=55°,
故答案为55°.
13.【解答】解:∵EF⊥AB,
∴∠AFE=∠C=90°,
在Rt△AEF和Rt△AEC中,
,
∴Rt△AEF≌Rt△AEC(HL),
∴∠AEF=∠AEC,
∵∠FEC=∠B+∠FEB=132°,
∴∠AEC=∠FEC=66°,
故答案为66°
14.【解答】解:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH
∴∠EAB=∠EFA=∠BGA=90°,
∵∠EAF+∠BAG=90°,∠ABG+∠BAG=90°
∴∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG
∴△EFA≌△ABG(AAS)
∴AF=BG,AG=EF.
同理证得△BGC≌△DHC得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+8+4+3=18
故S=(8+4)×18﹣3×4﹣8×3=72.
故答案为:72
15.【解答】解:∵∠C=90°,AQ⊥AC,
∴∠C=∠QAP=90°,
①当AP=3=BC时,
在Rt△ACB和Rt△QAP中,
∴Rt△ACB≌Rt△QAP(HL);
②当AP=8=AC时,
在Rt△ACB和Rt△PAQ中,
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:8或3.
三.解答题(共4小题)
16.【解答】解:BC与AE的位置关系是:BC∥AE;理由如下:
∵△ABC是等边三角形,
∴∠BAD=∠BCA=60°,AB=AC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠BAD=∠CAE=60°,
∴∠CAE=∠BCA,
∴BC∥AE.
17.【解答】证明:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
∵AB∥ED,
∴∠B=∠E,
∵AB=DE,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠A=∠D.
18.【解答】证明:(1)∵∠BAE=∠CAD,
∴∠BAD=∠CAE,
在△ABD与△ACE中,,
∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB
∴∠ABC﹣∠ABD=∠ACB﹣∠ACE,
即∠OBC=∠OCB,
∴OB=OC.
19.【解答】解:(1)①如图1,∵BA=BC,∠EBD=60°,
∴△ABC是等边三角形,
∴AD=AB=BC,∠DAB=∠ABC=60°,
∴∠EAD=∠FBD=120°,
∵DE=DF,
∴∠E=∠F,
在△AEC与△BCF中,,
∴△ADE≌△BDF(AAS),
∴AE=BF;
故答案为:AE=BF;
②证明:在BE上截取BG=BD,连接DG,
∵∠EBD=60°,BG=BD,
∴△GBD是等边三角形.
同理,△ABC也是等边三角形.
∴AG=CD,
∵DE=DF,∴∠E=∠F.
又∵∠DGB=∠DBG=60°,
∴∠DGE=∠DBF=120°,
在△DGE与△DBF中,,
∴△DGE≌△DBF(AAS),
∴GE=BF,
∴AE=BF+CD;
(2)如图3,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=EG﹣AG;
∴AE=BF﹣CD,
如图4,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=AG﹣EG;
∴AE=CD﹣BF
一.选择题
1.如图,已知点B、E、C、F在同一直线上,且BE=CF,∠ABC=∠DEF,那么添加一个条件后.仍无法判定△ABC≌△DEF的是( )
A.AC=DF
B.AB=DE
C.AC∥DF
D.∠A=∠D
2.如图,在△ABC和△DEF中,AB=DE,∠B=∠E,补充条件后,能直接应用“SAS”判定△ABC≌△DEF的是( )
A.∠A=∠D
B.∠ACB=∠DEF
C.AC=DF
D.BF=EC
3.如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD的度数为( )
A.110°
B.125°
C.130°
D.155°
4.如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS
B.SAS
C.SSA
D.ASA
5.如图,点B、F、C、E在一条直线上,AB∥DE,AC∥DF,那么添加下列一个条件后,仍无法判断△ABC≌△DEF的是( )
A.AB=DE
B.∠A=∠D
C.AC=DF
D.BF=EC
6.下列判定直角三角形全等的方法,不正确的是( )
A.两条直角边对应相等
B.斜边和一锐角对应相等
C.斜边和一直角边对应相等
D.两个直角三角形的面积相等
7.要测量河岸相对两点A、B的距离,已知AB垂直于河岸BF,先在BF上取两点C、D,使CD=CB,再过点D作BF的垂线段DE,使点A、C、E在一条直线上,如图,测出BD=10,ED=5,则AB的长是( )
A.2.5
B.10
C.5
D.以上都不对
8.下列叙述中:
①任意一个三角形的三条高至少有一条在此三角形内部;
②以a,b,c为边(a,b,c都大于0,且a+b>c)可以构成一个三角形;
③一个三角形内角之比为3:2:1,此三角形为直角三角形;
④有两个角和一条边对应相等的两个三角形全等;
正确的有( )个.
A.1
B.2
C.3
D.4
9.如图,已知线段AB=18米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走2米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A.4
B.6
C.4或9
D.6或9
10.如图,已知AF=AB,∠FAB=60°,AE=AC,∠EAC=60°,CF和BE交于O点,则下列结论:①CF=BE;②∠AMO=∠ANO;③OA平分∠FOE;④∠COB=120°,其中正确的有( )
A.1个
B.2个
C.3个
D.4个
二.填空题
11.如图,在△PAB中,PA=PB,M、N、K分别是PA、PB、AB上的点,且AM=BK,BN=AK.若∠MKN=50°,则∠P的度数为
.
12.如图,BD=CF,FD⊥BC于点D,DE⊥AB于点E,BE=CD,若∠AFD=145°,则∠EDF=
.
13.如图,在直角三角形ABC中,∠C=90°,∠B=42°,点E是BC上一点,EF⊥AB于点F,若EC=EF,则∠AEC的度数为
.
14.如图,已知AE⊥AB且AE=AB,BC⊥CD且BC=CD,按照图中所标注的数据,则图中阴影部分图形的面积S等于
.
15.如图,∠C=90°,AC=8,BC=3,线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到AP=
时,才能使△ABC与△APQ全等.
三.解答题
16.如图,△ABC是等边三角形,D是AC上一点,BD=CE,∠1=∠2,试判断BC与AE的位置关系,并证明你的结论.
17.如图,已知点B、F、C、E在一条直线上,BF=EC,AB∥ED,AB=DE.求证:∠A=∠D.
18.如图,在△ABC中,AB=AC,取点D与点E,使得AD=AE,∠BAE=∠CAD,连结BD与CE交于点O.求证:
(1)△ABD≌△ACE;
(2)OB=OC.
19.在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为
;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE,BF,CD之间的数量关系(直接写出结果,不需要证明).
参考答案与试题解析
一.选择题
1.【解答】解:
∵BE=CF,
∴BE+EC=EC+CF,即BC=EF,且∠ABC=∠DEF,
∴当AC=DF时,满足SSA,无法判定△ABC≌△DEF,故A不能;
当AB=DE时,满足SAS,可以判定△ABC≌△DEF,故B可以;
当AC∥DF时,可得∠ACB=∠F,满足ASA,可以判定△ABC≌△DEF,故C可以;
当∠A=∠D时,满足AAS,可以判定△ABC≌△DEF,故D可以;
故选:A.
2.【解答】解:补充BF=EC,理由如下:
∵BF=EC,
∴BC=EF,
在△ABC和△DEF中,,
∴△ABC≌△DEF(SAS),
故选:D.
3.【解答】解:
在△ACD和△BCE中
∴△ACD≌△BCE(SSS),
∴∠ACD=∠BCE,∠A=∠B,
∴∠BCA+∠ACE=∠ACE+∠ECD,
∴∠ACB=∠ECD=(∠BCD﹣∠ACE)=×(155°﹣55°)=50°,
∵∠B+∠ACB=∠A+∠APB,
∴∠APB=∠ACB=50°,
∴∠BPD=180°﹣50°=130°,
故选:C.
4.【解答】解:由图可知,三角形两角及夹边可以作出,
所以,依据是ASA.
故选:D.
5.【解答】解:∵AB∥DE,AC∥DF,
∴∠B=∠E,∠ACB=∠DFE,
A、添加AB=DE可利用AAS判断△ABC≌△DEF,故此选项不合题意;
B、添加∠A=∠D无法判断△ABC≌△DEF,故此选项符合题意;
C、添加AC=DF可利用AAS判断△ABC≌△DEF,故此选项不合题意;
D、添加BF=EC可得BC=EF,可利用ASA判断△ABC≌△DEF,故此选项不合题意;
故选:B.
6.【解答】解:如果在两个直角三角形中,两条直角边对应相等,
那么根据SAS即可判断两三角形全等,故选项A正确;
如果如果在两个直角三角形中,斜边和一锐角对应相等,
那么根据AAS可判断两三角形全等,故选项B正确;
如果如果在两个直角三角形中,斜边和一直角边对应相等,
那么根据HL可判断两三角形全等,故选项C正确;
如果两个直角三角形的面积相等,那么无法判定两个直角三角形全等,故D错误;
故选:D.
7.【解答】解:∵AB⊥BD,ED⊥AB,
∴∠ABC=∠EDC=90°,
在△ABC和△EDC中,,
∴△ABC≌△EDC(ASA),
∴AB=ED=5.
故选:C.
8.【解答】解:∵锐角三角形的三条高都在三角形的内部,直角三角形有一条高在三角形的内部,两条在三角形的两边上,钝角三角形的一条高在三角形的内部,两条高在三角形的外部,∴①正确;
∵当a=2,b=c=1时,满足a+b>c,但是边长为1、1、2不能组成三角形,∴②错误;
∵设三角形的三角为3x°,2x°,x°,
∴由三角形的内角和定理得:3x+2x+x=180,
∴x=30,
3x=90,即三角形是直角三角形,∴③正确;
∵有两个角和一条边对应相等的两个三角形全等,∴④正确;
故选:C.
9.【解答】解:当△APC≌△BQP时,AP=BQ,即18﹣x=2x,
解得:x=6;
当△APC≌△BPQ时,AP=BP=AB=9米,
此时所用时间为9秒,AC=BQ=18米,不合题意,舍去;
综上,出发6秒后,在线段MA上有一点C,使△CAP与△PBQ全等.
故选:B.
10.【解答】解:∵△ABF和△ACE是等边三角形,
∴AB=AF,AC=AE,∠FAB=∠EAC=60°,
∴∠FAB+∠BAC=∠EAC+∠BAC,
即∠FAC=∠BAE,
在△ABE与△AFC中,
,
∴△ABE≌△AFC(SAS),
∴BE=FC,故①正确,∠AEB=∠ACF,
∵∠EAN+∠ANE+∠AEB=180°,∠CON+∠CNO+∠ACF=180°,∠ANE=∠CNO
∴∠CON=∠CAE=60°=∠MOB,
∴∠BOC=180°﹣∠CON=120°,故④正确,
连AO,过A分别作AP⊥CF与P,AM⊥BE于Q,如图,
∵△ABE≌△AFC,
∴S△ABE=S△AFC,
∴CFAP=BEAQ,而CF=BE,
∴AP=AQ,
∴OA平分∠FOE,所以③正确,
∵∠AMO=∠MOB+∠ABE=60°+∠ABE,∠ANO=∠CON+∠ACF=60°+∠ACF,
显然∠ABE与∠ACF不一定相等,
∴∠AMO与∠ANO不一定相等,故②错误,
综上所述正确的有:①③④.
故选:C.
二.填空题(共5小题)
11.【解答】解:∵PA=PB,
∴∠A=∠B,
在△MAK和△KBN中,
,
∴△MAK≌△KBN(SAS),
∴∠AMK=∠BKN,
∵∠BKM=∠A+∠AMK=∠MKN+∠BKN,
∴∠A=∠MKN=50°,
∴∠A=∠B=50°,
∴∠P=180°﹣2×50°=80°.
故答案为80°.
12.【解答】解:∵FD⊥BC于点D,DE⊥AB于点E,
∴∠BED=∠FDC=90°,
∵BE=CD,BD=CF,
∴Rt△BED≌Rt△CDF(HL),
∴∠BDE=∠CFD,
∵∠AFD=145°,
∴∠DFC=35°,
∴∠BDE=35°,
∴∠EDF=90°﹣35°=55°,
故答案为55°.
13.【解答】解:∵EF⊥AB,
∴∠AFE=∠C=90°,
在Rt△AEF和Rt△AEC中,
,
∴Rt△AEF≌Rt△AEC(HL),
∴∠AEF=∠AEC,
∵∠FEC=∠B+∠FEB=132°,
∴∠AEC=∠FEC=66°,
故答案为66°
14.【解答】解:∵AE⊥AB且AE=AB,EF⊥FH,BG⊥FH
∴∠EAB=∠EFA=∠BGA=90°,
∵∠EAF+∠BAG=90°,∠ABG+∠BAG=90°
∴∠EAF=∠ABG,
∴AE=AB,∠EFA=∠AGB,∠EAF=∠ABG
∴△EFA≌△ABG(AAS)
∴AF=BG,AG=EF.
同理证得△BGC≌△DHC得GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+8+4+3=18
故S=(8+4)×18﹣3×4﹣8×3=72.
故答案为:72
15.【解答】解:∵∠C=90°,AQ⊥AC,
∴∠C=∠QAP=90°,
①当AP=3=BC时,
在Rt△ACB和Rt△QAP中,
∴Rt△ACB≌Rt△QAP(HL);
②当AP=8=AC时,
在Rt△ACB和Rt△PAQ中,
∴Rt△ACB≌Rt△PAQ(HL),
故答案为:8或3.
三.解答题(共4小题)
16.【解答】解:BC与AE的位置关系是:BC∥AE;理由如下:
∵△ABC是等边三角形,
∴∠BAD=∠BCA=60°,AB=AC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴∠BAD=∠CAE=60°,
∴∠CAE=∠BCA,
∴BC∥AE.
17.【解答】证明:∵BF=EC,
∴BF+FC=EC+FC,
∴BC=EF,
∵AB∥ED,
∴∠B=∠E,
∵AB=DE,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS),
∴∠A=∠D.
18.【解答】证明:(1)∵∠BAE=∠CAD,
∴∠BAD=∠CAE,
在△ABD与△ACE中,,
∴△ABD≌△ACE(SAS);
(2)∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB
∴∠ABC﹣∠ABD=∠ACB﹣∠ACE,
即∠OBC=∠OCB,
∴OB=OC.
19.【解答】解:(1)①如图1,∵BA=BC,∠EBD=60°,
∴△ABC是等边三角形,
∴AD=AB=BC,∠DAB=∠ABC=60°,
∴∠EAD=∠FBD=120°,
∵DE=DF,
∴∠E=∠F,
在△AEC与△BCF中,,
∴△ADE≌△BDF(AAS),
∴AE=BF;
故答案为:AE=BF;
②证明:在BE上截取BG=BD,连接DG,
∵∠EBD=60°,BG=BD,
∴△GBD是等边三角形.
同理,△ABC也是等边三角形.
∴AG=CD,
∵DE=DF,∴∠E=∠F.
又∵∠DGB=∠DBG=60°,
∴∠DGE=∠DBF=120°,
在△DGE与△DBF中,,
∴△DGE≌△DBF(AAS),
∴GE=BF,
∴AE=BF+CD;
(2)如图3,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=EG﹣AG;
∴AE=BF﹣CD,
如图4,连接DG,
由(1)知,GE=BF,AG=CD,
∴AE=AG﹣EG;
∴AE=CD﹣BF
