人教版数学九年级上册 24.2点和圆、直线和圆的位置关系同步测试试题(一) (word版 含解析)
文档属性
| 名称 | 人教版数学九年级上册 24.2点和圆、直线和圆的位置关系同步测试试题(一) (word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 222.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 20:36:59 | ||
图片预览

文档简介
点和圆、直线和圆的位置关系同步测试试题(一)
一.选择题
1.已知⊙O的半径r,圆心O到直线的距离为d,当d<r时,直线与⊙O的位置关系是( )
A.相交
B.相切
C.相离
D.以上都不对
2.关于下列四种说法中,你认为正确的有( )
①垂直于弦的直线一定经过圆心;
②经过直径外端的直线是圆的切线;
③对角互补的四边形四个顶点共圆;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分.
A.1个
B.2个
C.3个
D.4个
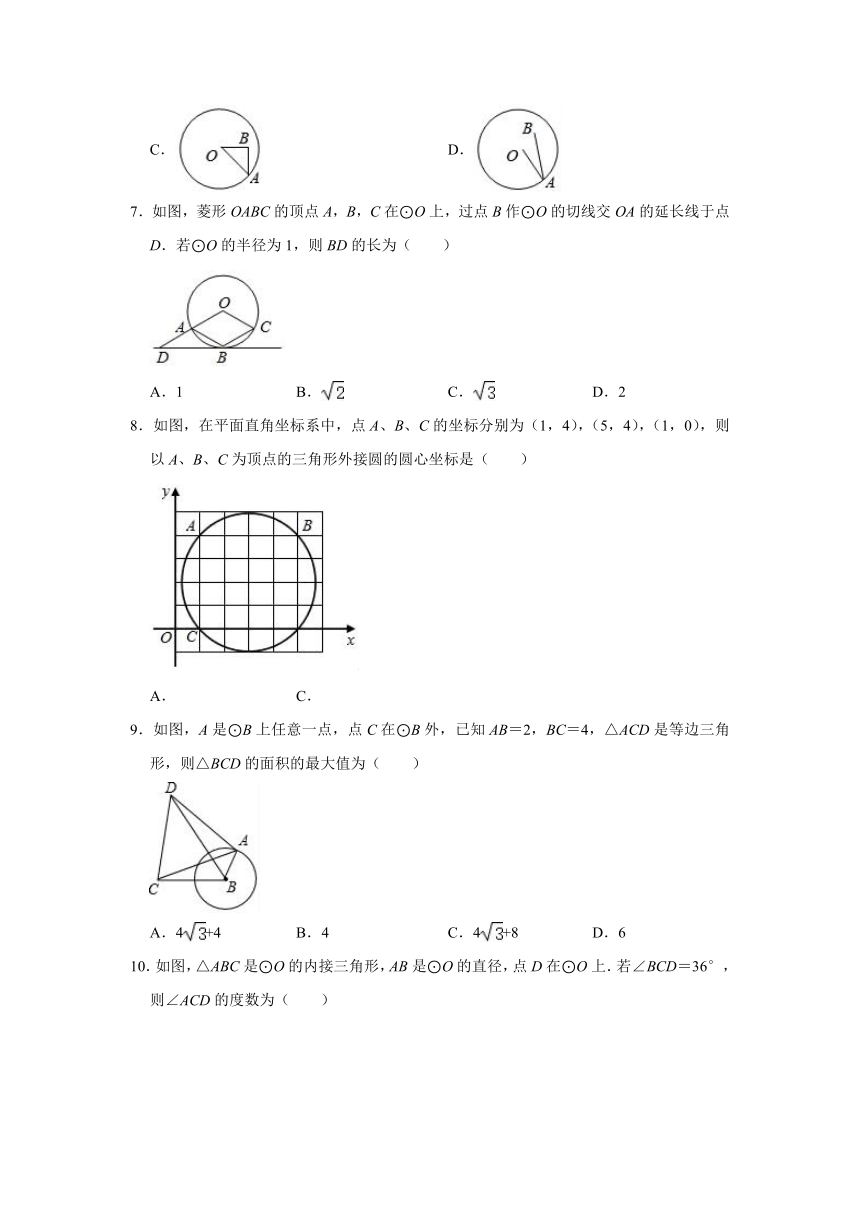
3.如图,BM为⊙O的切线,点B为切点,点A、C在⊙O上,连接AB、AC、BC,若∠MBA=130°,则∠ACB的度数为( )
A.40°
B.50°
C.60°
D.70°
4.已知⊙O的半径为3cm,且点P在⊙O外,则线段PO的长度为( )
A.等于6cm
B.大于3cm
C.小于3cm
D.等于3cm
5.若直线l与半径为10的⊙O相交,则圆心O与直线l的距离d为( )
A.d<10
B.d>10
C.d=10
D.d≤10
6.已知⊙O的半径OA长为1,OB=,则正确图形可能是( )
A.
B.
C.
D.
7.如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为( )
A.1
B.
C.
D.2
8.如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4),(5,4),(1,0),则以A、B、C为顶点的三角形外接圆的圆心坐标是( )
A.
C.
9.如图,A是⊙B上任意一点,点C在⊙B外,已知AB=2,BC=4,△ACD是等边三角形,则△BCD的面积的最大值为( )
A.4+4
B.4
C.4+8
D.6
10.如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,点D在⊙O上.若∠BCD=36°,则∠ACD的度数为( )
A.36°
B.44°
C.54°
D.64°
二.填空题
11.边长为3cm的等边三角形的外接圆半径是
.
12.Rt△ABC中,∠C=90°,AB=9,点G是△ABC的外心,则CG的长为
.
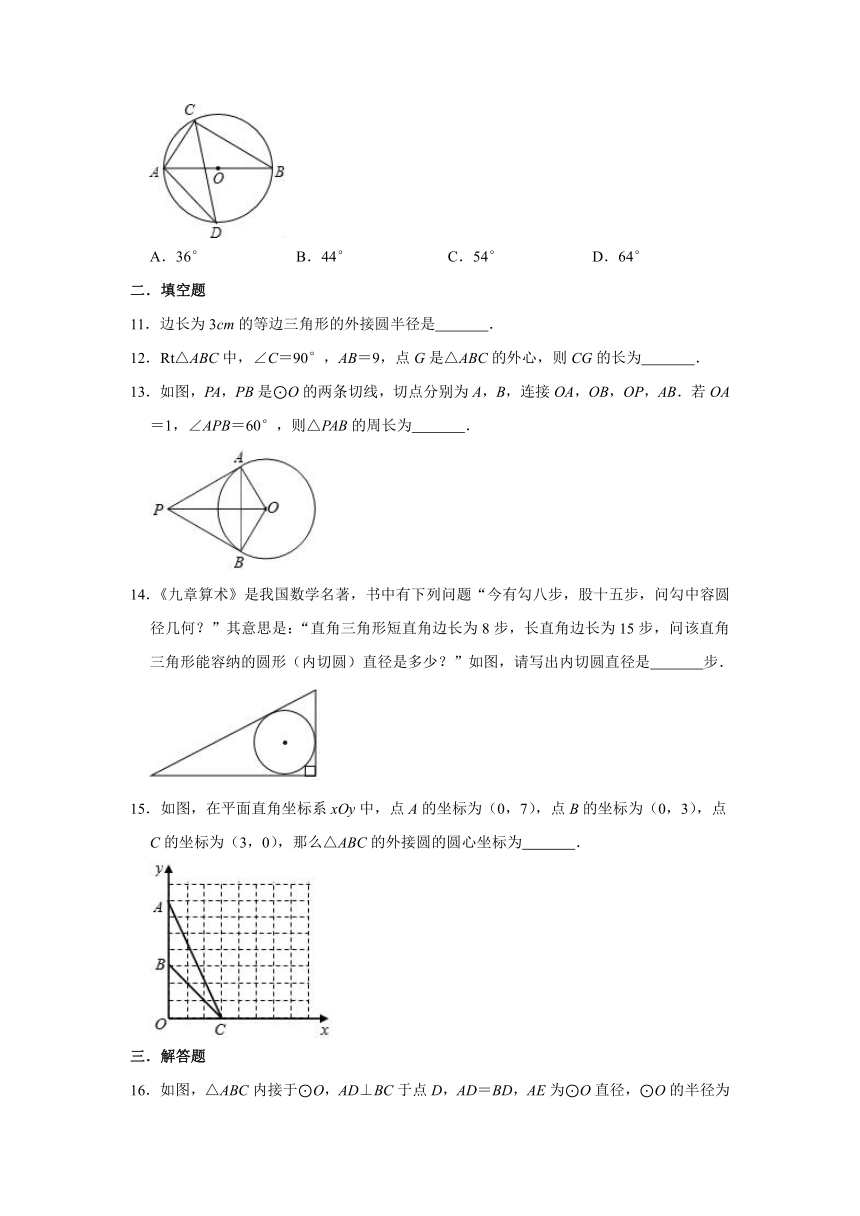
13.如图,PA,PB是⊙O的两条切线,切点分别为A,B,连接OA,OB,OP,AB.若OA=1,∠APB=60°,则△PAB的周长为
.
14.《九章算术》是我国数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“直角三角形短直角边长为8步,长直角边长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”如图,请写出内切圆直径是
步.
15.如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0),那么△ABC的外接圆的圆心坐标为
.
三.解答题
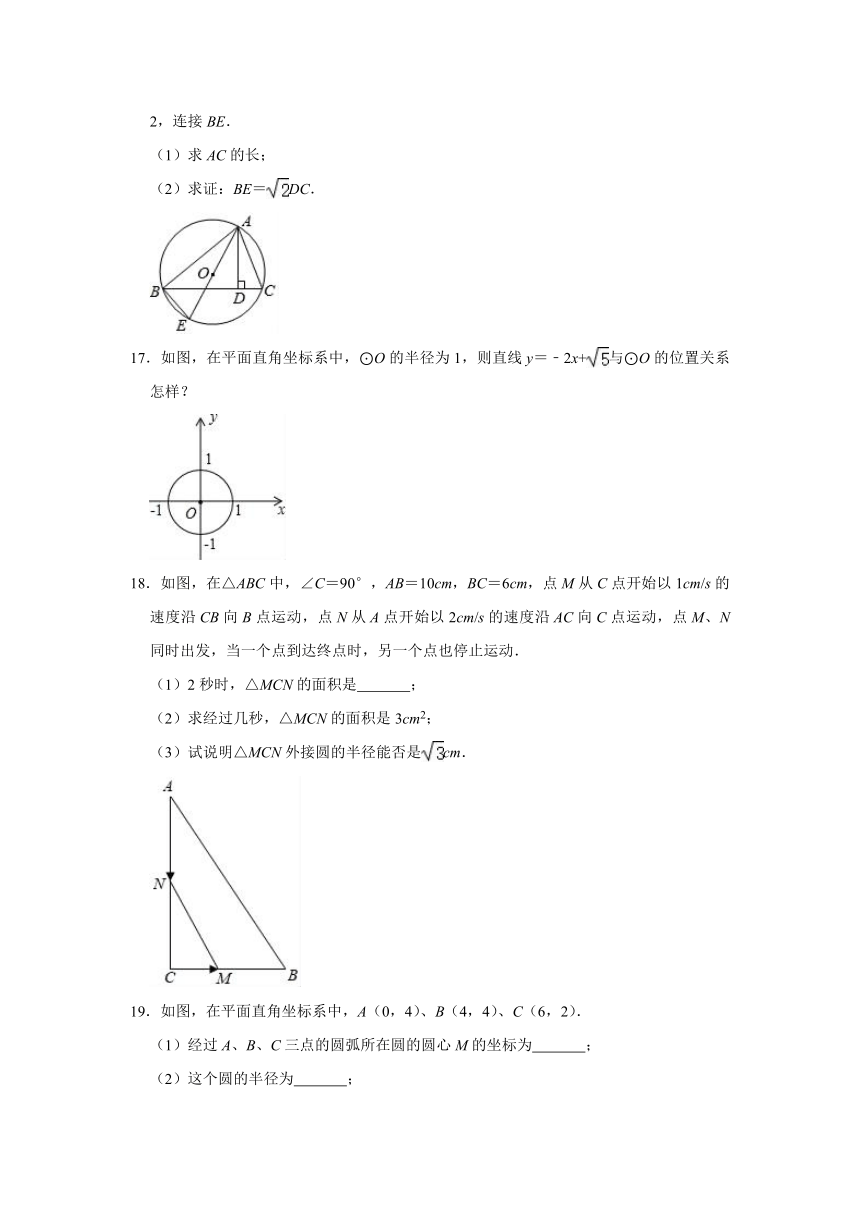
16.如图,△ABC内接于⊙O,AD⊥BC于点D,AD=BD,AE为⊙O直径,⊙O的半径为2,连接BE.
(1)求AC的长;
(2)求证:BE=DC.
17.如图,在平面直角坐标系中,⊙O的半径为1,则直线y=﹣2x+与⊙O的位置关系怎样?
18.如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,点M从C点开始以1cm/s的速度沿CB向B点运动,点N从A点开始以2cm/s的速度沿AC向C点运动,点M、N同时出发,当一个点到达终点时,另一个点也停止运动.
(1)2秒时,△MCN的面积是
;
(2)求经过几秒,△MCN的面积是3cm2;
(3)试说明△MCN外接圆的半径能否是cm.
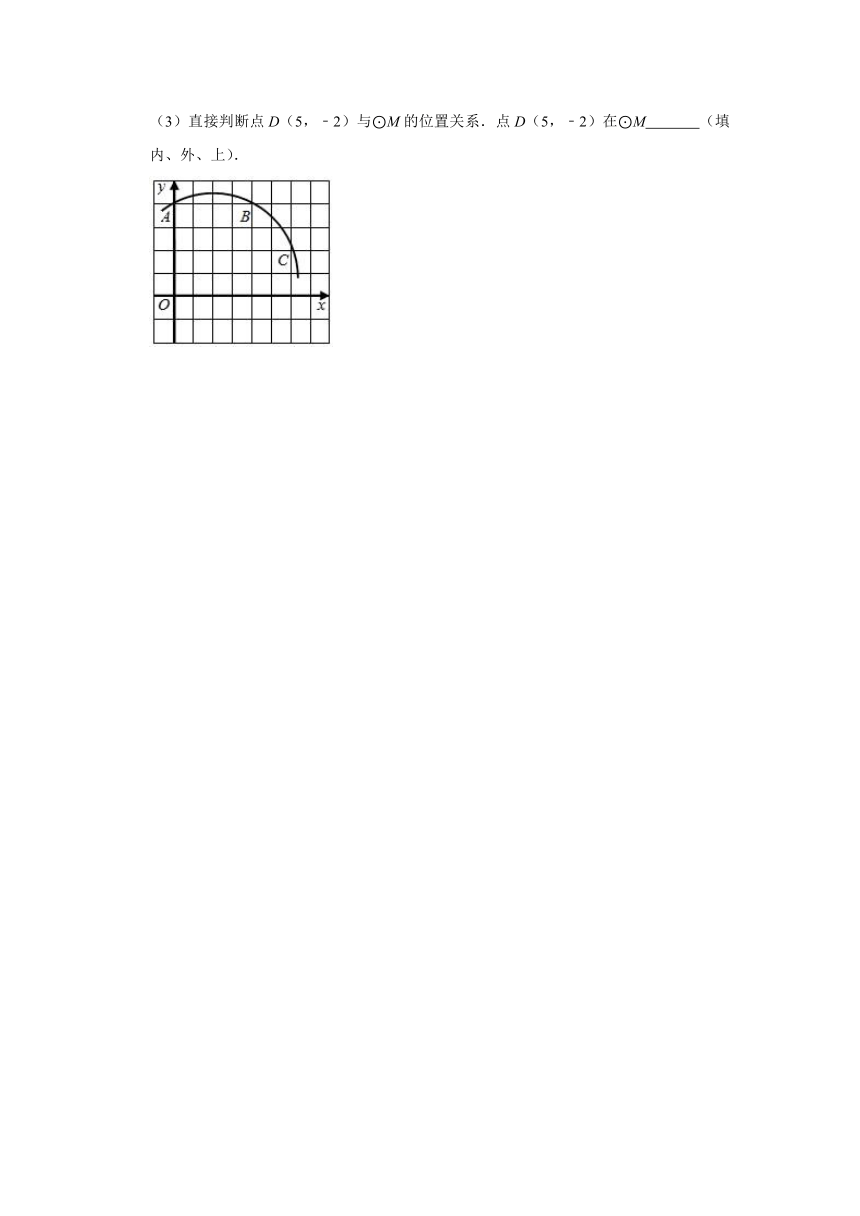
19.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为
;
(2)这个圆的半径为
;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M
(填内、外、上).
参考答案与试题解析
一.选择题
1.【解答】解:已知⊙O的半径r,圆心O到直线的距离为d,当d<r时,直线与⊙O的位置关系是相交,
故选:A.
2.【解答】解:①垂直平分弦的直线经过圆心,故①不符合题意;
②经过直径外端切垂直于这条直径的直线是圆的切线,故②不符合题意;
③对角互补的四边形四个顶点共圆;故③符合题意;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分,故④符合题意;
故选:B.
3.【解答】解:如图,连接OA,OB,
∵BM为⊙O的切线,
∴∠OBM=90°,
∵∠MBA=130°,
∴∠ABO=40°,
∵OA=OB,
∴∠BAO=∠ABO=40°,
∴∠AOB=180°﹣40°﹣40°=100°,
∴∠ACB=∠AOB=50°,
故选:B.
4.【解答】解:点P在⊙O外且⊙O的半径为3cm,
可知点P到圆心的距离大于r,即PO大于3,
故选:B.
5.【解答】解:∵⊙O的半径为10,直线l与⊙O相交,
∴圆心到直线的距离小于圆的半径,
即d<10.
故选:A.
6.【解答】解:∵⊙O的半径OA长为1,若OB=,
∴OA<OB,
∴点B在圆外,
故选:B.
7.【解答】解:连接OB,
∵BD是⊙O的切线,
∴∠OBD=90°,
∵四边形OABC为菱形,
∴OA=AB,
∵OA=OB,
∴OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠ODB=30°,
∴OD=2OB=2,
由勾股定理得,BD==,
故选:C.
8.【解答】解:根据垂径定理的推论,如图,
作弦AB、AC的垂直平分线,
交点O′即为三角形外接圆的圆心,
且O′坐标是(3,2).
故选:A.
9.【解答】解:以BC为边作等边△BCM,连接DM.
∵∠DCA=∠MCB=60°,
∴∠DCM=∠ACB,
∵DC=AC,MC=BC
∴△DCM≌△CAB(SAS),
∴DM=AB=2为定值,
即点D在以M为圆心,半径为2的圆上运动,
当点D运动至BC的中垂线与圆的交点时,
CB边上的高取最大值为2+2,
此时面积为4+4.
故选:A.
10.【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BCD=36°,
∴∠ACD=90°﹣∠BCD=54°.
故选:C.
二.填空题(共5小题)
11.【解答】解:如图,
∵等边三角形的边长为3cm,
∴AD=(cm),
∵∠DAO=∠BAC=60°×=30°,
∴AO==(cm).
故答案为:
cm.
12.【解答】解:因为Rt△ABC中,∠C=90°,AB=9,
点G是△ABC的外心,
所以CG是直角三角形ABC斜边的中线,
则CG的长为.
故答案为:.
13.【解答】解:∵PA,PB是⊙O的两条切线,
∴PA=PB,OA⊥PA,OP平分∠APB,
∵∠APB=60°,
∴∠APO=∠APB=30°,△PAB为等边三角形,
在Rt△OAP中,∵∠APO=30°,
∴PA=OA=,
∴△PAB的周长=3PA=3.
故答案为3.
14.【解答】解:根据题意,直角三角形的斜边为=17,
所以直角三角形的内切圆的半径==3,
所以直角三角形的内切圆的直径为6.
故答案为6.
15.【解答】解:如图,P点为△ABC的外接圆的圆心,其坐标为(5,5).
故答案为(5,5).
三.解答题(共4小题)
16.【解答】解:(1)如图,连接EC,
∵AD⊥BC于点D,AD=BD,
∴∠ABD=∠BAD=45°,
∴∠AEC=∠ABD=45°,
∵AE是⊙O的直径,
∴∠ACE=90°,
∵AE=4,
∴AC=AEsin45°=4×=2;
(2)证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ABE=∠ADC,
∵∠AEB=∠ACB,
∴△ABE∽△ADC,
∴BE:DC=AE:AC=4:2=,
∴BE=DC.
17.【解答】解:如图所示,过O作OC⊥直线AB,垂足为C,
在直线y=﹣2x+中,令x=0,解得:y=;令y=0,解得:x=,
∴A(,0),B(0,),即OA=,OB=,
在Rt△AOB中,根据勾股定理得:AB===,
又S△AOB=ABOC=OAOB,
∴OC===1,又圆O的半径为1,
则直线y=﹣2x+与圆O的位置关系是相切.
18.【解答】解:(1)∵∠C=90°,AB=10cm,BC=6cm,
∴AC==8,
根据题意得,AN=4,CM=2,
∴CN=4,
∴S△CMN=×4×2=4(cm2);
故答案为4cm2;
(2)设经过x秒,
根据题意得,(8﹣2x)x=3,
解得x1=1,x2=3;
即经过1秒或3秒,△MCN的面积是3cm2;
(3)∵△MNC为直角三角形,∠C=90°,
∴MN为△MCN外接圆的直径,
假设△MCN外接圆的半径为cm,则MN=2cm,
设M点运动的时间为t秒,则NC=8﹣2t,CM=t,
根据题意得,(8﹣2t)2+t2=(2)2,
整理得5t2﹣32t+52=0,
∵△=(﹣32)2﹣4×5×52=﹣16<0,
∴原方程没有实数解,
∴△MCN外接圆的半径不能是cm.
19.【解答】解:(1)如图,圆心M的坐标为(2,0);
(2)∵A(0,4),M(2,0),
∴MA==2,
即⊙M的半径为2;
(3)∵D(5,﹣2),M(2,0),
∴DM==
一.选择题
1.已知⊙O的半径r,圆心O到直线的距离为d,当d<r时,直线与⊙O的位置关系是( )
A.相交
B.相切
C.相离
D.以上都不对
2.关于下列四种说法中,你认为正确的有( )
①垂直于弦的直线一定经过圆心;
②经过直径外端的直线是圆的切线;
③对角互补的四边形四个顶点共圆;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分.
A.1个
B.2个
C.3个
D.4个
3.如图,BM为⊙O的切线,点B为切点,点A、C在⊙O上,连接AB、AC、BC,若∠MBA=130°,则∠ACB的度数为( )
A.40°
B.50°
C.60°
D.70°
4.已知⊙O的半径为3cm,且点P在⊙O外,则线段PO的长度为( )
A.等于6cm
B.大于3cm
C.小于3cm
D.等于3cm
5.若直线l与半径为10的⊙O相交,则圆心O与直线l的距离d为( )
A.d<10
B.d>10
C.d=10
D.d≤10
6.已知⊙O的半径OA长为1,OB=,则正确图形可能是( )
A.
B.
C.
D.
7.如图,菱形OABC的顶点A,B,C在⊙O上,过点B作⊙O的切线交OA的延长线于点D.若⊙O的半径为1,则BD的长为( )
A.1
B.
C.
D.2
8.如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4),(5,4),(1,0),则以A、B、C为顶点的三角形外接圆的圆心坐标是( )
A.
C.
9.如图,A是⊙B上任意一点,点C在⊙B外,已知AB=2,BC=4,△ACD是等边三角形,则△BCD的面积的最大值为( )
A.4+4
B.4
C.4+8
D.6
10.如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,点D在⊙O上.若∠BCD=36°,则∠ACD的度数为( )
A.36°
B.44°
C.54°
D.64°
二.填空题
11.边长为3cm的等边三角形的外接圆半径是
.
12.Rt△ABC中,∠C=90°,AB=9,点G是△ABC的外心,则CG的长为
.
13.如图,PA,PB是⊙O的两条切线,切点分别为A,B,连接OA,OB,OP,AB.若OA=1,∠APB=60°,则△PAB的周长为
.
14.《九章算术》是我国数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“直角三角形短直角边长为8步,长直角边长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?”如图,请写出内切圆直径是
步.
15.如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0),那么△ABC的外接圆的圆心坐标为
.
三.解答题
16.如图,△ABC内接于⊙O,AD⊥BC于点D,AD=BD,AE为⊙O直径,⊙O的半径为2,连接BE.
(1)求AC的长;
(2)求证:BE=DC.
17.如图,在平面直角坐标系中,⊙O的半径为1,则直线y=﹣2x+与⊙O的位置关系怎样?
18.如图,在△ABC中,∠C=90°,AB=10cm,BC=6cm,点M从C点开始以1cm/s的速度沿CB向B点运动,点N从A点开始以2cm/s的速度沿AC向C点运动,点M、N同时出发,当一个点到达终点时,另一个点也停止运动.
(1)2秒时,△MCN的面积是
;
(2)求经过几秒,△MCN的面积是3cm2;
(3)试说明△MCN外接圆的半径能否是cm.
19.如图,在平面直角坐标系中,A(0,4)、B(4,4)、C(6,2).
(1)经过A、B、C三点的圆弧所在圆的圆心M的坐标为
;
(2)这个圆的半径为
;
(3)直接判断点D(5,﹣2)与⊙M的位置关系.点D(5,﹣2)在⊙M
(填内、外、上).
参考答案与试题解析
一.选择题
1.【解答】解:已知⊙O的半径r,圆心O到直线的距离为d,当d<r时,直线与⊙O的位置关系是相交,
故选:A.
2.【解答】解:①垂直平分弦的直线经过圆心,故①不符合题意;
②经过直径外端切垂直于这条直径的直线是圆的切线,故②不符合题意;
③对角互补的四边形四个顶点共圆;故③符合题意;
④圆外一点引圆的两条切线,两切点的连线被该点与圆心连线垂直平分,故④符合题意;
故选:B.
3.【解答】解:如图,连接OA,OB,
∵BM为⊙O的切线,
∴∠OBM=90°,
∵∠MBA=130°,
∴∠ABO=40°,
∵OA=OB,
∴∠BAO=∠ABO=40°,
∴∠AOB=180°﹣40°﹣40°=100°,
∴∠ACB=∠AOB=50°,
故选:B.
4.【解答】解:点P在⊙O外且⊙O的半径为3cm,
可知点P到圆心的距离大于r,即PO大于3,
故选:B.
5.【解答】解:∵⊙O的半径为10,直线l与⊙O相交,
∴圆心到直线的距离小于圆的半径,
即d<10.
故选:A.
6.【解答】解:∵⊙O的半径OA长为1,若OB=,
∴OA<OB,
∴点B在圆外,
故选:B.
7.【解答】解:连接OB,
∵BD是⊙O的切线,
∴∠OBD=90°,
∵四边形OABC为菱形,
∴OA=AB,
∵OA=OB,
∴OA=OB=AB,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠ODB=30°,
∴OD=2OB=2,
由勾股定理得,BD==,
故选:C.
8.【解答】解:根据垂径定理的推论,如图,
作弦AB、AC的垂直平分线,
交点O′即为三角形外接圆的圆心,
且O′坐标是(3,2).
故选:A.
9.【解答】解:以BC为边作等边△BCM,连接DM.
∵∠DCA=∠MCB=60°,
∴∠DCM=∠ACB,
∵DC=AC,MC=BC
∴△DCM≌△CAB(SAS),
∴DM=AB=2为定值,
即点D在以M为圆心,半径为2的圆上运动,
当点D运动至BC的中垂线与圆的交点时,
CB边上的高取最大值为2+2,
此时面积为4+4.
故选:A.
10.【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BCD=36°,
∴∠ACD=90°﹣∠BCD=54°.
故选:C.
二.填空题(共5小题)
11.【解答】解:如图,
∵等边三角形的边长为3cm,
∴AD=(cm),
∵∠DAO=∠BAC=60°×=30°,
∴AO==(cm).
故答案为:
cm.
12.【解答】解:因为Rt△ABC中,∠C=90°,AB=9,
点G是△ABC的外心,
所以CG是直角三角形ABC斜边的中线,
则CG的长为.
故答案为:.
13.【解答】解:∵PA,PB是⊙O的两条切线,
∴PA=PB,OA⊥PA,OP平分∠APB,
∵∠APB=60°,
∴∠APO=∠APB=30°,△PAB为等边三角形,
在Rt△OAP中,∵∠APO=30°,
∴PA=OA=,
∴△PAB的周长=3PA=3.
故答案为3.
14.【解答】解:根据题意,直角三角形的斜边为=17,
所以直角三角形的内切圆的半径==3,
所以直角三角形的内切圆的直径为6.
故答案为6.
15.【解答】解:如图,P点为△ABC的外接圆的圆心,其坐标为(5,5).
故答案为(5,5).
三.解答题(共4小题)
16.【解答】解:(1)如图,连接EC,
∵AD⊥BC于点D,AD=BD,
∴∠ABD=∠BAD=45°,
∴∠AEC=∠ABD=45°,
∵AE是⊙O的直径,
∴∠ACE=90°,
∵AE=4,
∴AC=AEsin45°=4×=2;
(2)证明:∵AE是⊙O的直径,
∴∠ABE=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠ABE=∠ADC,
∵∠AEB=∠ACB,
∴△ABE∽△ADC,
∴BE:DC=AE:AC=4:2=,
∴BE=DC.
17.【解答】解:如图所示,过O作OC⊥直线AB,垂足为C,
在直线y=﹣2x+中,令x=0,解得:y=;令y=0,解得:x=,
∴A(,0),B(0,),即OA=,OB=,
在Rt△AOB中,根据勾股定理得:AB===,
又S△AOB=ABOC=OAOB,
∴OC===1,又圆O的半径为1,
则直线y=﹣2x+与圆O的位置关系是相切.
18.【解答】解:(1)∵∠C=90°,AB=10cm,BC=6cm,
∴AC==8,
根据题意得,AN=4,CM=2,
∴CN=4,
∴S△CMN=×4×2=4(cm2);
故答案为4cm2;
(2)设经过x秒,
根据题意得,(8﹣2x)x=3,
解得x1=1,x2=3;
即经过1秒或3秒,△MCN的面积是3cm2;
(3)∵△MNC为直角三角形,∠C=90°,
∴MN为△MCN外接圆的直径,
假设△MCN外接圆的半径为cm,则MN=2cm,
设M点运动的时间为t秒,则NC=8﹣2t,CM=t,
根据题意得,(8﹣2t)2+t2=(2)2,
整理得5t2﹣32t+52=0,
∵△=(﹣32)2﹣4×5×52=﹣16<0,
∴原方程没有实数解,
∴△MCN外接圆的半径不能是cm.
19.【解答】解:(1)如图,圆心M的坐标为(2,0);
(2)∵A(0,4),M(2,0),
∴MA==2,
即⊙M的半径为2;
(3)∵D(5,﹣2),M(2,0),
∴DM==
同课章节目录
