人教版数学九年级上册 24.3正多边形和圆同步测试试题(一) (word版 含解析)
文档属性
| 名称 | 人教版数学九年级上册 24.3正多边形和圆同步测试试题(一) (word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 283.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 00:00:00 | ||
图片预览

文档简介
正多边形和圆同步测试试题(一)
一.选择题
1.下面说法正确的个数有( )
①若m>n,则ma2>nb2;
②由三条线段首尾顺次相接所组成的图形叫做三角形;
③有两个角互余的三角形一定是直角三角形;
④各边都相等的多边形是正多边形;
⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形一定是钝角三角形.
A.1
个
B.2
个
C.3
个
D.4
个
2.下列说法,错误的是( )
A.为了解一种灯泡的使用寿命,宜采用普查的方法
B.一元二次方程3x2﹣2x﹣1=0有两个不相等的实数根
C.一次函数y=﹣3x+2的图象经过第一、二、四象限
D.正六边形每个内角的度数是外角度数的2倍
3.如图,正五边形ABCDE内接于⊙O,点P是劣弧上一点(点P不与点C重合),则∠CPD=( )
A.45°
B.36°
C.35°
D.30°
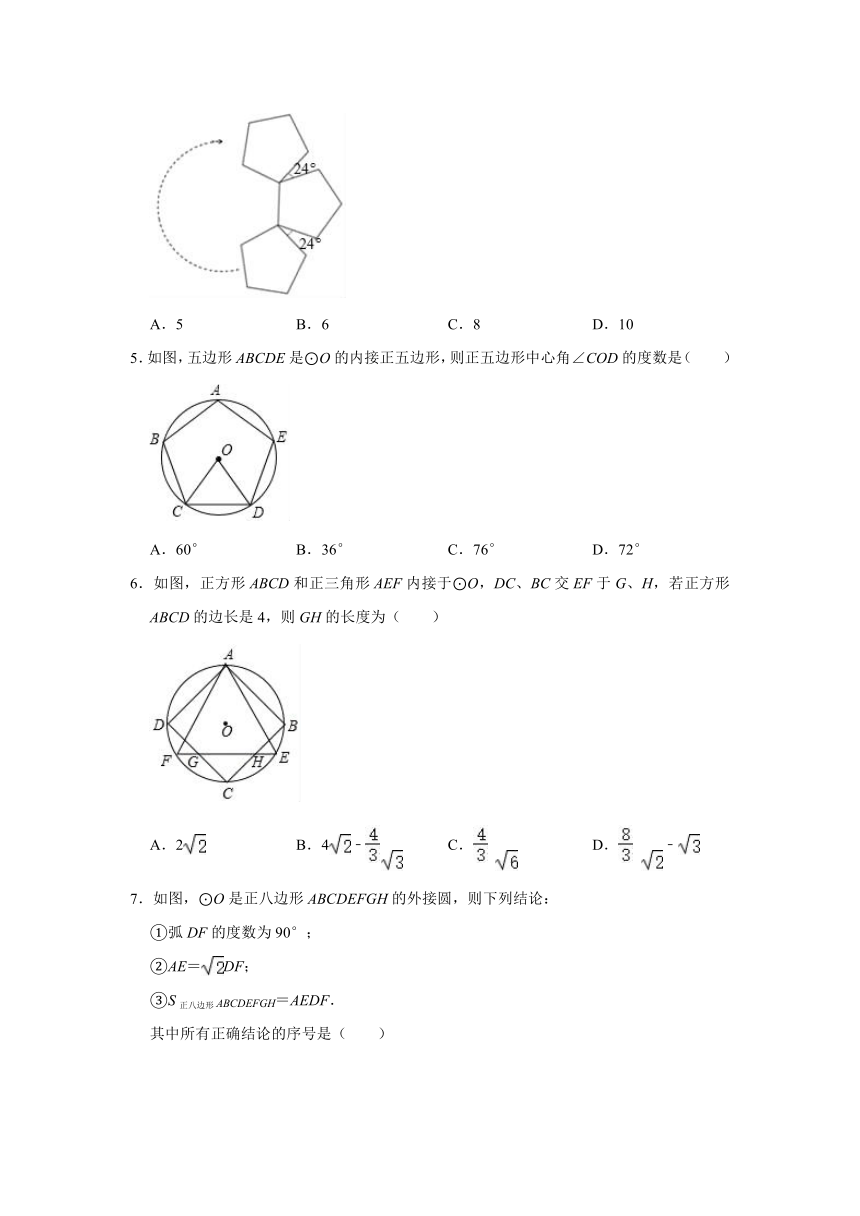
4.如图,用若n个全等的正五边形按如下方式拼接可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为24°,图中所示的是前3个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形,则n的值为( )
A.5
B.6
C.8
D.10
5.如图,五边形ABCDE是⊙O的内接正五边形,则正五边形中心角∠COD的度数是( )
A.60°
B.36°
C.76°
D.72°
6.如图,正方形ABCD和正三角形AEF内接于⊙O,DC、BC交EF于G、H,若正方形ABCD的边长是4,则GH的长度为( )
A.2
B.4﹣
C.
D.
﹣
7.如图,⊙O是正八边形ABCDEFGH的外接圆,则下列结论:
①弧DF的度数为90°;
②AE=DF;
③S正八边形ABCDEFGH=AEDF.
其中所有正确结论的序号是( )
A.①②
B.①③
C.②③
D.①②③
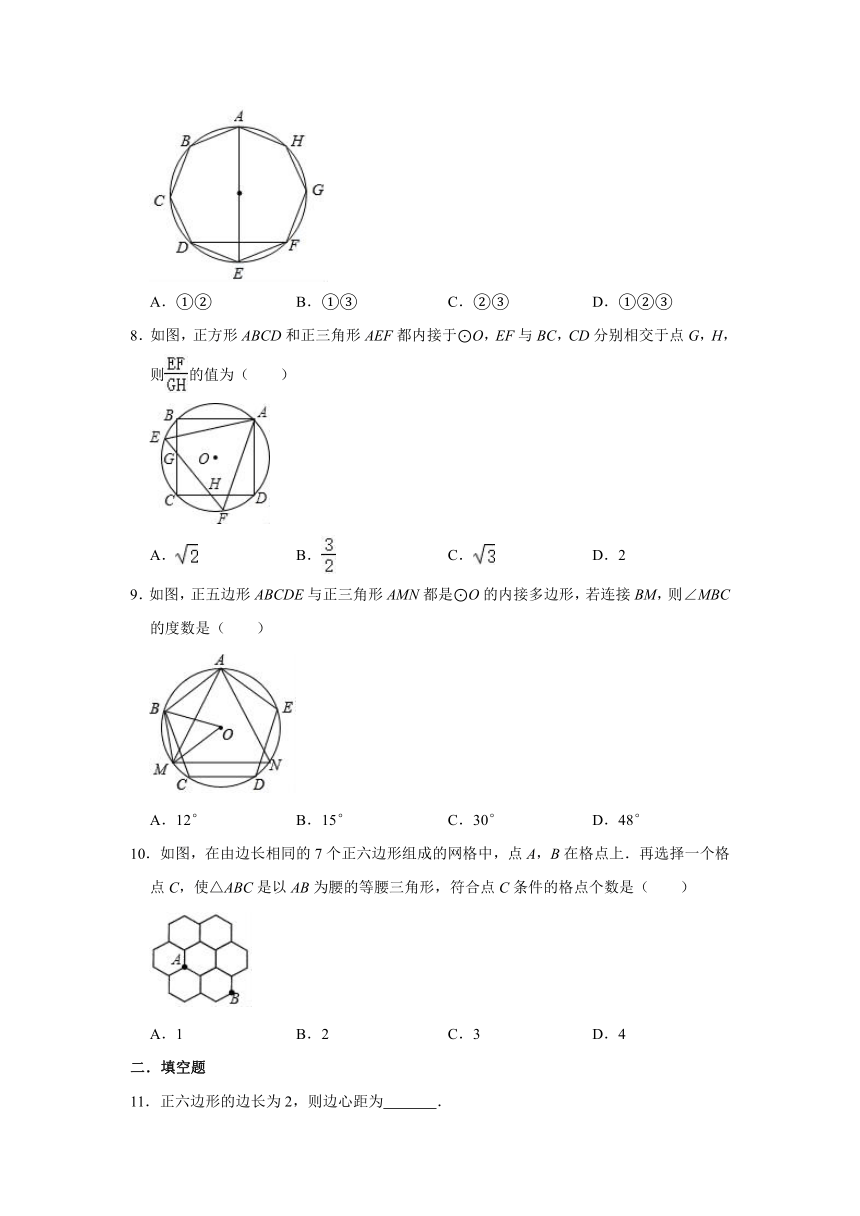
8.如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则的值为( )
A.
B.
C.
D.2
9.如图,正五边形ABCDE与正三角形AMN都是⊙O的内接多边形,若连接BM,则∠MBC的度数是( )
A.12°
B.15°
C.30°
D.48°
10.如图,在由边长相同的7个正六边形组成的网格中,点A,B在格点上.再选择一个格点C,使△ABC是以AB为腰的等腰三角形,符合点C条件的格点个数是( )
A.1
B.2
C.3
D.4
二.填空题
11.正六边形的边长为2,则边心距为
.
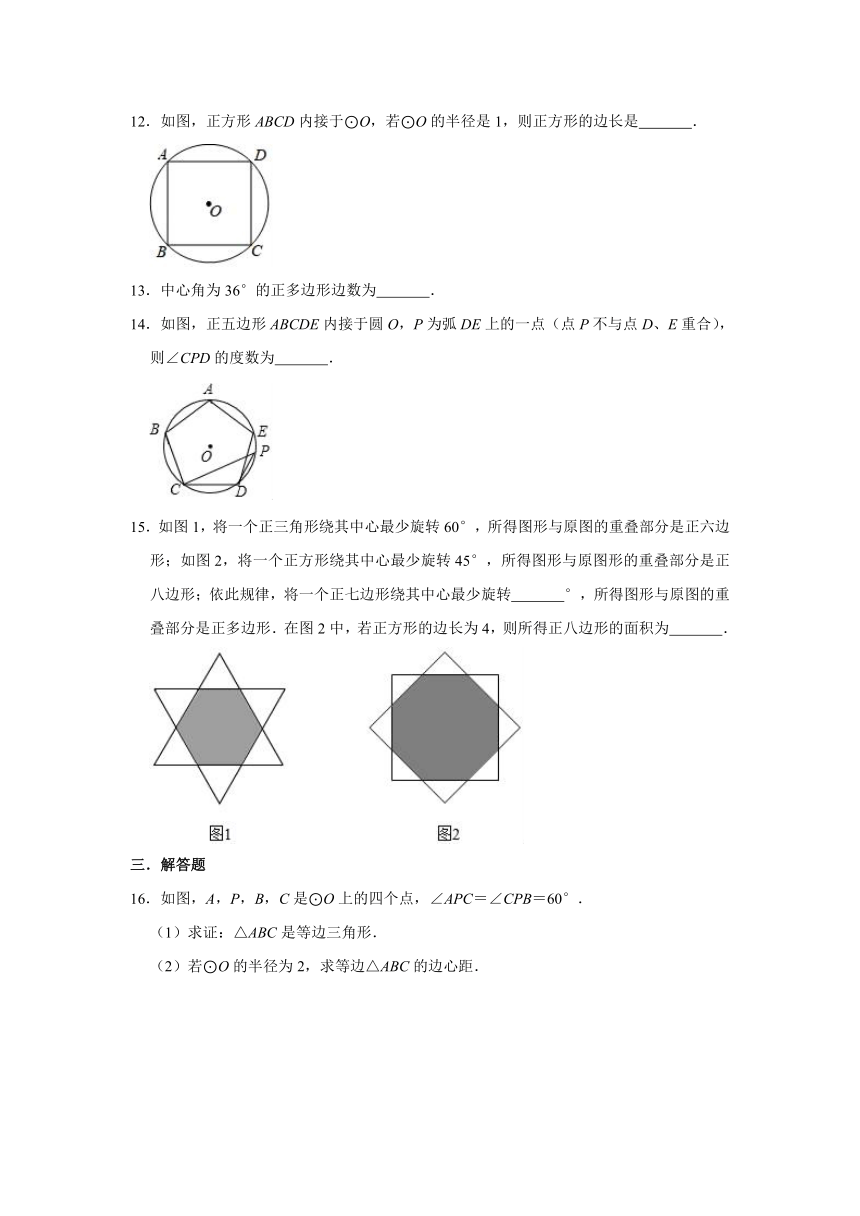
12.如图,正方形ABCD内接于⊙O,若⊙O的半径是1,则正方形的边长是
.
13.中心角为36°的正多边形边数为
.
14.如图,正五边形ABCDE内接于圆O,P为弧DE上的一点(点P不与点D、E重合),则∠CPD的度数为
.
15.如图1,将一个正三角形绕其中心最少旋转60°,所得图形与原图的重叠部分是正六边形;如图2,将一个正方形绕其中心最少旋转45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转
°,所得图形与原图的重叠部分是正多边形.在图2中,若正方形的边长为4,则所得正八边形的面积为
.
三.解答题
16.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
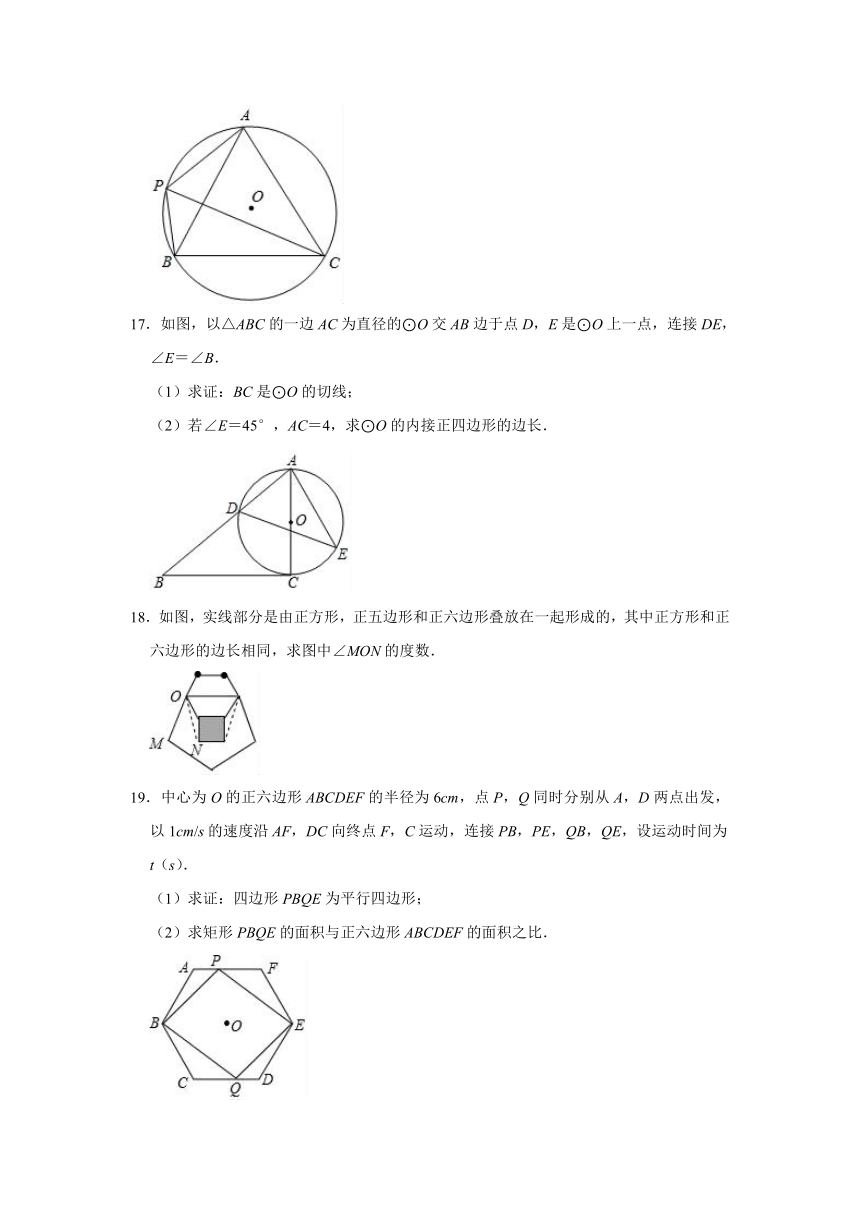
17.如图,以△ABC的一边AC为直径的⊙O交AB边于点D,E是⊙O上一点,连接DE,∠E=∠B.
(1)求证:BC是⊙O的切线;
(2)若∠E=45°,AC=4,求⊙O的内接正四边形的边长.
18.如图,实线部分是由正方形,正五边形和正六边形叠放在一起形成的,其中正方形和正六边形的边长相同,求图中∠MON的度数.
19.中心为O的正六边形ABCDEF的半径为6cm,点P,Q同时分别从A,D两点出发,以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间为t(s).
(1)求证:四边形PBQE为平行四边形;
(2)求矩形PBQE的面积与正六边形ABCDEF的面积之比.
参考答案与试题解析
一.选择题
1.【解答】解:①若m>n,则ma2>nb2,当a=0时错误;故不符合题意;
②由不在同一直线上的三条线段首尾
顺次相接所组成的图形叫做三角形,故不符合题意;
③有两个角互余的三角形一定是直角三角形,故符合题意;
④各边都相等,各角也相等的多边形是正多边形,故不符合题意.
⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形是钝角三角形或直角三角形,故不符合题意;
故选:A.
2.【解答】解:A、为了解一种灯泡的使用寿命,此调查具有破坏性,宜采用抽查的方法;故此选项符合题意;
B、一元二次方程3x2﹣2x﹣1=0有两个不相等的实数根;故此选项不符合题意;
C、一次函数y=﹣3x+2的图象经过第一、二、四象限;故此选项不符合题意;
D、正六边形每个内角的度数是外角度数的2倍;故此选项不符合题意;
故选:A.
3.【解答】解:如图,连接OC,OD,
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
故选:B.
4.【解答】解:∵正五边形的每个内角为:=108°,
∴组成的正多边形的每个内角为:360°﹣2×108°﹣24°=120°,
∵n个全等的正五边形拼接可以拼成一个环状,中间会形成一个正多边形,
∴组成的正多边形为正n边形,
则=120°,
解得:n=6,
故选:B.
5.【解答】解:∵五边形ABCDE是⊙O的内接正五边形,
∴五边形ABCDE的中心角∠COD的度数为=72°,
故选:D.
6.【解答】解:连接AC交EF于M,连接OF,
∵四边形ABCD是正方形,
∴∠B=90°,
∴AC是⊙O的直径,
∴△ACD是等腰直角三角形,
∴AC=AD=4,
∴OA=OC=2,
∵△AEF是等边三角形,
∴AM⊥EF,∠OFM=30°,
∴OM=OF=,
∴CM=,
∴∠ACD=45°,∠CMG=90°,
∴∠CGM=45°,
∴△CGH是等腰直角三角形,
∴GH=2CM=2.
故选:A.
7.【解答】解:设圆心为O,连接OD,OF,
∵∠DOE=∠EOF==45°,
∴∠DOF=90°,
∴弧DF的度数为90°,
∴①正确;
∵∠DOF=90°,OD=OF,
∴2OD2=DF2,
∴OD=,
∵AE=2OD,
∴AE=DF,
∴②正确;
∵S四边形ODEF=DFOE,
∴S正八边形ABCDEFGH=4S四边形ODEF=2DFOE,
∵OE=AE,
∴S正八边形ABCDEFGH=AEDF,
∴③正确;
故选:D.
8.【解答】解:如图,连接AC、BD、OF,
设⊙O的半径是r,
则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴FI=rsin60°=r,
∴EF=r×2=r,
∵AO=2OI,
∴OI=r,CI=r﹣r=r,
∴==,
∴GH=BD=r,
∴==.
故选:C.
9.【解答】解:连接OA、OC.
∵五边形ABCDE是正五边形,
∴∠AOB==72°,
∴∠AOC=72°×2=144°,
∵△AMN是正三角形,
∴∠AOM==120°,
∴∠COM=∠AOC﹣∠AOM=144°﹣120°=24°,
∴∠MBC=∠COM=×24°=12°.
故选:A.
10.【解答】解:AB的长等于六边形的边长+最长对角线的长,
据此可以确定共有2个点C,位置如图,
故选:B.
二.填空题(共5小题)
11.【解答】解:如图所示:
连接OA、OB,作OC⊥AB于C,
则∠OCA=90°,AC=BC=AB=1,∠AOB=60°,
∴∠AOC=30°,
∴OC=AC=;
故答案为:.
12.【解答】解:连接OB,OC,则OC=OB=1,∠BOC=90°,
在Rt△BOC中,BC==.
∴正方形的边长是,
故答案为:.
13.【解答】解:由题意可得:
∵360°÷36°=10,
∴它的边数是10.
故答案为10.
14.【解答】解:如图,连接OC,OD.
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
故答案为:36°.
15.【解答】解:如图2所示:
将一个正三角形绕其中心最少旋转60°,所得图形与原图的重叠部分是正六边形;将一个正方形绕其中心最少旋转45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转,所得图形与原图的重叠部分是正多边形.
在图2中,由题意得:PM=MN=NQ,AM=AP=BN=BQ,
则MN=PM=AM,
∵AM+MN+BN=AB=4,
∴AM+AM+AM=4,
解得:AM=4﹣2,
则所得正八边形的面积为4×4﹣4××(4﹣2)2=32﹣32;
故答案为:(),32﹣32.
三.解答题(共4小题)
16.【解答】(1)证明:在⊙O中,
∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
17.【解答】解:(1)证明:连接CD,
∵AC为直径,
∴∠ADC=90°,
∵∠E=∠ACD,
∠E=∠B.
∴∠ACD=∠B,
∴∠ACD+∠CAD=∠B+∠CAD=90°,
∴∠ACB=90°,
∴BC是⊙O的切线;
(2)如图,
连接OD、CE,
若∠E=45°,
则∠AOD=90°,
∵AC=4,
∴OA=OD=2,
∴AD=2.
∴⊙O的内接正四边形的边长为AD的长为2.
18.【解答】解:由正方形、正五边形和正六边形的性质得,∠AOM=108°,∠OBC=120°,∠NBC=90°,
∴∠AOB=×120°=60°,∠MOB=108°﹣60°=48°,
∴∠OBN=360°﹣120°﹣90°=150°,
∴∠NOB=×(180°﹣150°)=15°,
∴∠MON=33°.
19.【解答】(1)证明:∵六边形ABCDEF是正六边形,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,
∴AP=DQ=t,PF=QC=6﹣t,
在△ABP和△DEQ中,,
∴△ABP≌△DEQ(SAS),
∴BP=EQ,
同理可证PE=QB,
∴四边形PEQB为平行四边形.
(2)解:连接BE、OA,则∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=6,BE=2OB=12,
当t=0时,点P与A重合,Q与D重合,四边形PBQE即为四边形ABDE,如图1所示:
则∠EAF=∠AEF=30°,
∴∠BAE=120°﹣30°=90°,
∴此时四边形ABDE是矩形,即四边形PBQE是矩形.
当t=6时,点P与F重合,Q与C重合,四边形PBQE即为四边形FBCE,如图2所示:
同法可知∠BFE=90°,此时四边形PBQE是矩形.
综上所述,t=0s或6s时,四边形PBQE是矩形,
∴AE==6,
∴矩形PBQE的面积=矩形ABDE的面积=AB×AE=6×6=36;
∵正六边形ABCDEF的面积=6△AOB的面积=6×矩形ABDE的面积=6××36
一.选择题
1.下面说法正确的个数有( )
①若m>n,则ma2>nb2;
②由三条线段首尾顺次相接所组成的图形叫做三角形;
③有两个角互余的三角形一定是直角三角形;
④各边都相等的多边形是正多边形;
⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形一定是钝角三角形.
A.1
个
B.2
个
C.3
个
D.4
个
2.下列说法,错误的是( )
A.为了解一种灯泡的使用寿命,宜采用普查的方法
B.一元二次方程3x2﹣2x﹣1=0有两个不相等的实数根
C.一次函数y=﹣3x+2的图象经过第一、二、四象限
D.正六边形每个内角的度数是外角度数的2倍
3.如图,正五边形ABCDE内接于⊙O,点P是劣弧上一点(点P不与点C重合),则∠CPD=( )
A.45°
B.36°
C.35°
D.30°
4.如图,用若n个全等的正五边形按如下方式拼接可以拼成一个环状,使相邻的两个正五边形有公共顶点,所夹的锐角为24°,图中所示的是前3个正五边形的拼接情况,拼接一圈后,中间会形成一个正多边形,则n的值为( )
A.5
B.6
C.8
D.10
5.如图,五边形ABCDE是⊙O的内接正五边形,则正五边形中心角∠COD的度数是( )
A.60°
B.36°
C.76°
D.72°
6.如图,正方形ABCD和正三角形AEF内接于⊙O,DC、BC交EF于G、H,若正方形ABCD的边长是4,则GH的长度为( )
A.2
B.4﹣
C.
D.
﹣
7.如图,⊙O是正八边形ABCDEFGH的外接圆,则下列结论:
①弧DF的度数为90°;
②AE=DF;
③S正八边形ABCDEFGH=AEDF.
其中所有正确结论的序号是( )
A.①②
B.①③
C.②③
D.①②③
8.如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则的值为( )
A.
B.
C.
D.2
9.如图,正五边形ABCDE与正三角形AMN都是⊙O的内接多边形,若连接BM,则∠MBC的度数是( )
A.12°
B.15°
C.30°
D.48°
10.如图,在由边长相同的7个正六边形组成的网格中,点A,B在格点上.再选择一个格点C,使△ABC是以AB为腰的等腰三角形,符合点C条件的格点个数是( )
A.1
B.2
C.3
D.4
二.填空题
11.正六边形的边长为2,则边心距为
.
12.如图,正方形ABCD内接于⊙O,若⊙O的半径是1,则正方形的边长是
.
13.中心角为36°的正多边形边数为
.
14.如图,正五边形ABCDE内接于圆O,P为弧DE上的一点(点P不与点D、E重合),则∠CPD的度数为
.
15.如图1,将一个正三角形绕其中心最少旋转60°,所得图形与原图的重叠部分是正六边形;如图2,将一个正方形绕其中心最少旋转45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转
°,所得图形与原图的重叠部分是正多边形.在图2中,若正方形的边长为4,则所得正八边形的面积为
.
三.解答题
16.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
17.如图,以△ABC的一边AC为直径的⊙O交AB边于点D,E是⊙O上一点,连接DE,∠E=∠B.
(1)求证:BC是⊙O的切线;
(2)若∠E=45°,AC=4,求⊙O的内接正四边形的边长.
18.如图,实线部分是由正方形,正五边形和正六边形叠放在一起形成的,其中正方形和正六边形的边长相同,求图中∠MON的度数.
19.中心为O的正六边形ABCDEF的半径为6cm,点P,Q同时分别从A,D两点出发,以1cm/s的速度沿AF,DC向终点F,C运动,连接PB,PE,QB,QE,设运动时间为t(s).
(1)求证:四边形PBQE为平行四边形;
(2)求矩形PBQE的面积与正六边形ABCDEF的面积之比.
参考答案与试题解析
一.选择题
1.【解答】解:①若m>n,则ma2>nb2,当a=0时错误;故不符合题意;
②由不在同一直线上的三条线段首尾
顺次相接所组成的图形叫做三角形,故不符合题意;
③有两个角互余的三角形一定是直角三角形,故符合题意;
④各边都相等,各角也相等的多边形是正多边形,故不符合题意.
⑤如果一个三角形只有一条高在三角形的内部,那么这个三角形是钝角三角形或直角三角形,故不符合题意;
故选:A.
2.【解答】解:A、为了解一种灯泡的使用寿命,此调查具有破坏性,宜采用抽查的方法;故此选项符合题意;
B、一元二次方程3x2﹣2x﹣1=0有两个不相等的实数根;故此选项不符合题意;
C、一次函数y=﹣3x+2的图象经过第一、二、四象限;故此选项不符合题意;
D、正六边形每个内角的度数是外角度数的2倍;故此选项不符合题意;
故选:A.
3.【解答】解:如图,连接OC,OD,
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
故选:B.
4.【解答】解:∵正五边形的每个内角为:=108°,
∴组成的正多边形的每个内角为:360°﹣2×108°﹣24°=120°,
∵n个全等的正五边形拼接可以拼成一个环状,中间会形成一个正多边形,
∴组成的正多边形为正n边形,
则=120°,
解得:n=6,
故选:B.
5.【解答】解:∵五边形ABCDE是⊙O的内接正五边形,
∴五边形ABCDE的中心角∠COD的度数为=72°,
故选:D.
6.【解答】解:连接AC交EF于M,连接OF,
∵四边形ABCD是正方形,
∴∠B=90°,
∴AC是⊙O的直径,
∴△ACD是等腰直角三角形,
∴AC=AD=4,
∴OA=OC=2,
∵△AEF是等边三角形,
∴AM⊥EF,∠OFM=30°,
∴OM=OF=,
∴CM=,
∴∠ACD=45°,∠CMG=90°,
∴∠CGM=45°,
∴△CGH是等腰直角三角形,
∴GH=2CM=2.
故选:A.
7.【解答】解:设圆心为O,连接OD,OF,
∵∠DOE=∠EOF==45°,
∴∠DOF=90°,
∴弧DF的度数为90°,
∴①正确;
∵∠DOF=90°,OD=OF,
∴2OD2=DF2,
∴OD=,
∵AE=2OD,
∴AE=DF,
∴②正确;
∵S四边形ODEF=DFOE,
∴S正八边形ABCDEFGH=4S四边形ODEF=2DFOE,
∵OE=AE,
∴S正八边形ABCDEFGH=AEDF,
∴③正确;
故选:D.
8.【解答】解:如图,连接AC、BD、OF,
设⊙O的半径是r,
则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴FI=rsin60°=r,
∴EF=r×2=r,
∵AO=2OI,
∴OI=r,CI=r﹣r=r,
∴==,
∴GH=BD=r,
∴==.
故选:C.
9.【解答】解:连接OA、OC.
∵五边形ABCDE是正五边形,
∴∠AOB==72°,
∴∠AOC=72°×2=144°,
∵△AMN是正三角形,
∴∠AOM==120°,
∴∠COM=∠AOC﹣∠AOM=144°﹣120°=24°,
∴∠MBC=∠COM=×24°=12°.
故选:A.
10.【解答】解:AB的长等于六边形的边长+最长对角线的长,
据此可以确定共有2个点C,位置如图,
故选:B.
二.填空题(共5小题)
11.【解答】解:如图所示:
连接OA、OB,作OC⊥AB于C,
则∠OCA=90°,AC=BC=AB=1,∠AOB=60°,
∴∠AOC=30°,
∴OC=AC=;
故答案为:.
12.【解答】解:连接OB,OC,则OC=OB=1,∠BOC=90°,
在Rt△BOC中,BC==.
∴正方形的边长是,
故答案为:.
13.【解答】解:由题意可得:
∵360°÷36°=10,
∴它的边数是10.
故答案为10.
14.【解答】解:如图,连接OC,OD.
∵ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°,
故答案为:36°.
15.【解答】解:如图2所示:
将一个正三角形绕其中心最少旋转60°,所得图形与原图的重叠部分是正六边形;将一个正方形绕其中心最少旋转45°,所得图形与原图形的重叠部分是正八边形;依此规律,将一个正七边形绕其中心最少旋转,所得图形与原图的重叠部分是正多边形.
在图2中,由题意得:PM=MN=NQ,AM=AP=BN=BQ,
则MN=PM=AM,
∵AM+MN+BN=AB=4,
∴AM+AM+AM=4,
解得:AM=4﹣2,
则所得正八边形的面积为4×4﹣4××(4﹣2)2=32﹣32;
故答案为:(),32﹣32.
三.解答题(共4小题)
16.【解答】(1)证明:在⊙O中,
∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
17.【解答】解:(1)证明:连接CD,
∵AC为直径,
∴∠ADC=90°,
∵∠E=∠ACD,
∠E=∠B.
∴∠ACD=∠B,
∴∠ACD+∠CAD=∠B+∠CAD=90°,
∴∠ACB=90°,
∴BC是⊙O的切线;
(2)如图,
连接OD、CE,
若∠E=45°,
则∠AOD=90°,
∵AC=4,
∴OA=OD=2,
∴AD=2.
∴⊙O的内接正四边形的边长为AD的长为2.
18.【解答】解:由正方形、正五边形和正六边形的性质得,∠AOM=108°,∠OBC=120°,∠NBC=90°,
∴∠AOB=×120°=60°,∠MOB=108°﹣60°=48°,
∴∠OBN=360°﹣120°﹣90°=150°,
∴∠NOB=×(180°﹣150°)=15°,
∴∠MON=33°.
19.【解答】(1)证明:∵六边形ABCDEF是正六边形,
∴AB=BC=CD=DE=EF=FA,∠A=∠ABC=∠C=∠D=∠DEF=∠F,
∵点P,Q同时分别从A,D两点出发,以1cm/s速度沿AF,DC向终点F,C运动,
∴AP=DQ=t,PF=QC=6﹣t,
在△ABP和△DEQ中,,
∴△ABP≌△DEQ(SAS),
∴BP=EQ,
同理可证PE=QB,
∴四边形PEQB为平行四边形.
(2)解:连接BE、OA,则∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=6,BE=2OB=12,
当t=0时,点P与A重合,Q与D重合,四边形PBQE即为四边形ABDE,如图1所示:
则∠EAF=∠AEF=30°,
∴∠BAE=120°﹣30°=90°,
∴此时四边形ABDE是矩形,即四边形PBQE是矩形.
当t=6时,点P与F重合,Q与C重合,四边形PBQE即为四边形FBCE,如图2所示:
同法可知∠BFE=90°,此时四边形PBQE是矩形.
综上所述,t=0s或6s时,四边形PBQE是矩形,
∴AE==6,
∴矩形PBQE的面积=矩形ABDE的面积=AB×AE=6×6=36;
∵正六边形ABCDEF的面积=6△AOB的面积=6×矩形ABDE的面积=6××36
同课章节目录
