苏科版七年级上册第四章《一元一次方程》应用题分类:分类计费问题综合练习(二)(Word版 含解析)
文档属性
| 名称 | 苏科版七年级上册第四章《一元一次方程》应用题分类:分类计费问题综合练习(二)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 30.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 09:45:41 | ||
图片预览




文档简介
《一元一次方程》应用题分类:分类计费问题综合练习
1.公园门票价格规定如下表:
购票张数
1~50张
51~100张
100张以上
每张票的价格
13元
11元
9元
某校七(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)如果两班联合起来,作为一个团体购票,可省多少钱?
(2)两班各有多少学生?
(3)如果七(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
2.某果品公司将一批不易存放的水果从A地运往B地销售,现有两家运输公司可供选择,这两家公司提供的信息如下:
运输公司
运输速度(千米/小时)
运输费用(元/千米)
装卸时间(小时)
装卸费用(元)
甲公司
60
6
4
1600
乙公司
a
8
b
1000
现已知乙公司的运输速度比甲公司的运输速度慢10千米/小时,但装卸时间比甲公司少2小时,两家运输公司的运输及装卸的费用总和相等.
(1)填空:a=
,b=
.
(2)求A、B两地之间的路程;
(3)若这批不易存放的水果在运输与装卸的过程中的损耗为300元/小时,请你算出果品公司选择这两家公司所需的总费用(运输费、装卸费、损耗费三项之和)分别是多少元,并指出从经济角度应选择哪一家公司.
3.缴纳个人所得税是收入达到缴纳标准的公民应居的义务,个人所得税率是由国家相应的法律法规规定的.根据个人的收入计算,新修改的《中华人民共和国个人所得税法》于2019年1月1日正式实施,新税法规定个人所得税的免征额为5000元,应纳税所得额按如下税率表缴纳个人所得税(应纳税所得额=税前收总额﹣国家规定扣除专项金额﹣免征额).
级数
应纳税所得额
税率%
1
不超过3000元的
3
2
超过3000元至12000元的部分
10
3
超过12000元至25000元的部分
20
…
…
…
根据以上信息,解决以下问题:
(1)小明的妈妈应纳税所得额为2000元,她应该缴纳个人所得税
元.
(2)小明的爸爸要缴纳个人所得税590元,他应纳税所得额是多少元?
(3)如果小明的爸爸和妈妈某月应纳税所得额共为20000元(爸爸的应纳税所得额高于妈妈的应纳税所得额),共要缴纳个人所得税1780元,小明的爸爸应纳税所得额是
元.
4.某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m2时,按2元/m2计算:月用水量超过20m2时,其中的20m2仍按2元/m2计算,超过部分按2.6元/m2计算.设某户家庭月用水量xm2
(1)用含x的式子表示:
当0≤x≤20时,水费为
元;当x>20时,水费为
元;
(2)
月份
4月
5月
6月
用水量
15
17
a
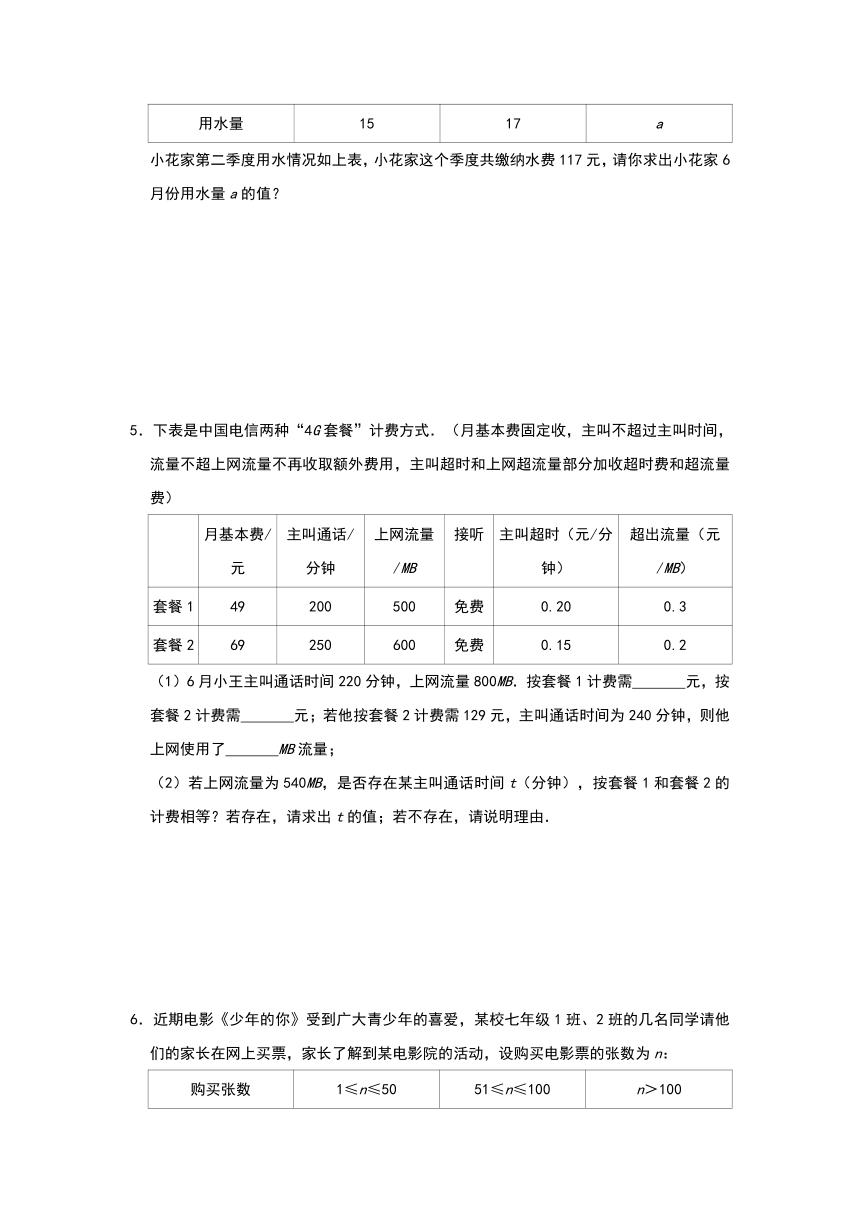
小花家第二季度用水情况如上表,小花家这个季度共缴纳水费117元,请你求出小花家6月份用水量a的值?
5.下表是中国电信两种“4G套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用,主叫超时和上网超流量部分加收超时费和超流量费)
月基本费/元
主叫通话/分钟
上网流量/MB
接听
主叫超时(元/分钟)
超出流量(元/MB)
套餐1
49
200
500
免费
0.20
0.3
套餐2
69
250
600
免费
0.15
0.2
(1)6月小王主叫通话时间220分钟,上网流量800MB.按套餐1计费需
元,按套餐2计费需
元;若他按套餐2计费需129元,主叫通话时间为240分钟,则他上网使用了
MB流量;
(2)若上网流量为540MB,是否存在某主叫通话时间t(分钟),按套餐1和套餐2的计费相等?若存在,请求出t的值;若不存在,请说明理由.
6.近期电影《少年的你》受到广大青少年的喜爱,某校七年级1班、2班的几名同学请他们的家长在网上买票,家长了解到某电影院的活动,设购买电影票的张数为n:
购买张数
1≤n≤50
51≤n≤100
n>100
每张票的价格
38元
30元
26元
家长沟通后决定两个班的同学在期中考试结束后去观看.两个班共有104人,其中1班人数多于40不足50人.经过估算,如果两个班都以班为单位购买,则一共应付3504元.
(1)求两个班各有多少同学?
(2)如果两个班联合起来,作为一个团体购票,可以节省多少钱?
(3)如果七年级1班同学作为一个团体购票,你认为如何购票才最省钱?可以节省多少钱?
7.阅读材料:为落实水资源管理制度,大力促进水资源节约,本市居民用水实行阶梯水价,按年度用水量计算,将居民家庭全年用水量划分为三档,水价分档递增,实施细则如表:
北京市居民用水阶梯水价表
(单位:元/立方米)
供水类型
阶梯
户年用水量(立方米)
水价
自来水
第一阶梯
0﹣150(含)
5
第二阶梯
151﹣260(含)
7
第三阶梯
260以上
9
如某居民去年用水量为160立方米,则其应缴纳水费为150×5+(160﹣150)×7=820元.
(1)若小明家去年用水量为100立方米,则小明家应缴纳的水费为
元;
(2)若小明家全年用水x立方米,且总量不超过240立方米,则应缴纳的水费为
元?(用含x的代数式表示);
(3)若小明家今年全年共纳水费925元,则小明家共用水多少立方米?
8.某市居民使用自来水按如下标准收费(水费按月缴纳)
户月用水量
单价
不超过12m3的部分
2元/m3
超过12m3但不超过20m3的部分
3元/m3
超过20m3的部分
4元/m3
(1)某用户一个月用了14m3水,求该用户这个月应缴纳的水费
(2)某户月用水量为n立方米(12<n≤20),该用户缴纳的水费是39元,列方程求n的值
(3)甲、乙两用户一个月共用水40m3,设甲用户用水量为xm3,且12<x≤28
①当12<x≤20时,甲、乙两用户一个月共缴纳的水费为
元(用含x的整式表示)
②当20<x≤28时,甲、乙两用户一个月共缴纳的水费为
元(用含x的整式表示)
9.为充分发挥市场机制和价格杠杆在水资源配置中的作用,促进节约用水,提高用水效率,
7月1日起某地实行阶梯水价,价目如表(注:水费按月结算,m3表示立方米):
价目表
每月用水量
单价(元/m3)
不超过18的部分
3
超出18不超出25的部分
4
超出25的部分
7
例:某户居民5月份共用水23m3,则应缴水费3×18+4×(23﹣18)=74(元).
(1)若A居民家1月份共用水12m3,则应缴水费
元;
(2)若B居民家2月份共缴水费66元,则用水
m3;
(3)若C居民家3月份用水量为am3(a低于20m3,即a<20),且C居民家3、4两个月用水量共40m3,求3、4两个月共缴水费多少元?(用含a的代数式表示,不要求化简)
(4)在(3)中,当a=19时,求C居民家3、4两个月共缴水费多少元?
10.某市出租车收费标准如下表所示,根据此收费标准,解决下列问题:
行驶路程
收费标准
不超出3km的部分
起步价7元+燃油附加费1元
超出3km不超出6km的部分
1.6元/km
超出6km的部分
2.4元/km
(1)若行驶路程为5km,则打车费用为
元;
(2)若行驶路程为xkm(x>6),则打车费用为
元(用含x的代数式表示);
(3)当打车费用为32元时,行驶路程为多少千米?
参考答案
1.解:(1)1240﹣104×9=304,
∴可省304元钱;
(2)设七(1)班有x人,
则有13x+11(104﹣x)=1240或13x+9(104﹣x)=1240,
解得:x=48或x=76(不合题意,舍去).
即七(1)班48人,七(2)班56人;
(3)要想享受优惠,由(1)可知七(1)班48人,只需多买3张,
51×11=561,48×13=624>561
∴48人买51人的票可以更省钱.
2.解:(1)依题意,得:60﹣a=10,4﹣b=2,
解得:a=50,b=2.
故答案为:50;2.
(2)设A、B两地之间的路程为s千米,
依题意,得:6s+1600=8s+1000,
解得:s=300.
答:A、B两地之间的路程为300千米.
(3)选择甲公司所需的总费用为300×6+1600+300×(300÷60+4)=6100(元),
选择乙公司所需的总费用为300×8+1000+300×(300÷50+4)=6400(元).
∵6100<6400,
∴选择甲公司总费用更少.
3.解:(1)由题意知,2000×3%=60(元)
故答案是:60;
(2)易知:小明爸爸在第2级中的税,设他的应纳税所得额为a元,则
90+(a﹣3000)×10%=590.
解得a=8000.
∴小明爸爸应纳税所得额为8000元
(3)设小明的爸爸应纳税所得额是x元,则小明的妈妈应纳税所得额是(20000﹣x)元,则10000<x<20000
①当10000<x<12000时,则90+(x﹣3000)×10%+90+(20000﹣x﹣3000)×10%=1780,无解,舍去;
②当12000<x<17000时,则90+(12000﹣3000)×10%+(x﹣12000)×20%+90+(20000﹣x﹣3000)×10%=1780.
解得x=14000.
③当17000<x<20000时,则90+(12000﹣3000)×10%+(x﹣12000)×20%+(20000﹣x)×3%=1780.
解得x=,舍去.
综上所述,小明的爸爸应纳税所得额是
14000元.
故答案是:14000.
4.解:(1)当0≤x≤20时,水费为2x元;当x>20时,水费为20×2+2.6(x﹣20)=(2.6x﹣12)元.
故答案为:2x、(2.6x﹣12);
(2)由题意得,小花家4月份,5月份共交水费15×2+17×2=30+34=64(元),则6月份用水量a>20,
∴小花家6月份的用水为a吨,则超过20吨的部分为(a﹣20)吨,
∴15×2+17×2+20×2+2.6(a﹣20)=117,
解得:a=25.
答:小花家6月份用水25吨.
5.解:(1)套餐1:
49+0.2×(220﹣200)+0.3×(800﹣500)
=49+0.2×20+0.3×300
=49+4+90
=143.
套餐2:
69+0.2×(800﹣600)
=69+0.2×200
=69+40
=109.
设上网流量为xMB,则
69+0.2(x﹣600)=129
解得x=900.
故答案为:143;109;900.
(2)当0≤t<200时,
49+0.3×(540﹣500)=61≠69
∴此时不存在这样的t.
当200≤t≤250时,
49+0.2(t﹣200)+0.3×(540﹣500)=69
解得t=240.
当t>250时,
49+0.2(t﹣200)+0.3×(540﹣500)=69+0.15(t﹣250)
解得t=210(舍).
故若上网流量为540MB,当主叫通话时间为240分钟时,按套餐1和套餐2的计费相等.
6.解:(1)设1班有x名同学,则2班有(104﹣x)名学生,
依题意,得:38x+30(104﹣x)=3504,
解得:x=48,
∴104﹣x=56.
答:1班有48名同学,2班有56名学生.
(2)26×104=2704(元),
3504﹣2704=800(元).
答:可以节省800元钱.
(3)购买48张票所需费用为38×48=1824(元),
购买51张票所需费用为30×51=1530(元).
1824>1530,1824﹣1530=294(元).
答:购买51张门票最省钱,可以节省294元钱.
7.解:(1)100×5=500(元).
故答案为:500.
(2)当0<x≤150时,应缴纳水费为5x元;
当150<x≤240时,应缴纳水费为150×5+(x﹣150)×7=(7x﹣300)元.
故答案为:.
(3)150×5=750(元),150×5+(260﹣150)×7=1520(元).
∵750<925<1520,
∴150<x<260.
依题意,得:7x﹣300=925,
解得:x=175.
答:小明家共用水175立方米.
8.解:(1)由题意可得:2×12+3×(14﹣12)=30元,
答:该用户这个月应缴纳30元水费.
(2)由题意可得,2×12+3(n﹣12)=39,
解得n=17;
(3)①∵12<x≤20,
∴乙用户用水量20≤40﹣x<28,
∴12×2+3(x﹣12)+12×2+3×8+4(40﹣x﹣20)=(116﹣x)元;
②∵20<x≤28,
∴乙用户用水量12≤40﹣x<20,
∴12×2+3×8+4(x﹣20)+12×2+3(40﹣x﹣12)=(x+76)元;
故答案为(116﹣x)元,(x+76)元.
9.解:(1)∵12<18,
∴应缴水费12×3=36(元),
故答案为:36;
(2)设B居民家2月份用水xm3,
∴3×18+4×(x﹣18)=66,
解得x=21.
故答案为:21.
(3)①当a<15时,4月份的用水量超过25m3
共缴水费:3a+3×18+4(25﹣18)+7(40﹣a﹣25)=187﹣4a,
②当15≤a≤18时,4月份的用水量不低于22m3且不超过25m3
共缴水费:3a+3×18+4(40﹣a﹣18)=142﹣a,
③当18<a≤20时,4月份的用水量超过20m3且不超过22m3
共缴水费:3×18+4(a﹣18)+3×18+4(40﹣a﹣18)=124,
(4)当a=19时,C居民家3、4两个月共缴水费124元.
10.解:(1)支付车费:7+1+(5﹣3)×1.6=11.2(元),
故答案为:11.2;
(2)7+1+1.6×3+2.4(x﹣6)
=8+4.8+2.4x﹣14.4
=2.4x﹣1.6(元),
故答案为:(2.4x﹣1.6);
(3)设当打车费用为32元时,行驶路程为x千米,
由题意得:2.4x﹣1.6=32,
解得:x=14,
∴当打车费用为32元时,行驶路程为14千米.
1.公园门票价格规定如下表:
购票张数
1~50张
51~100张
100张以上
每张票的价格
13元
11元
9元
某校七(1)、(2)两个班共104人去游公园,其中(1)班人数较少,不足50人.经估算,如果两个班都以班为单位购票,则一共应付1240元,问:
(1)如果两班联合起来,作为一个团体购票,可省多少钱?
(2)两班各有多少学生?
(3)如果七(1)班单独组织去游公园,作为组织者的你将如何购票才最省钱?
2.某果品公司将一批不易存放的水果从A地运往B地销售,现有两家运输公司可供选择,这两家公司提供的信息如下:
运输公司
运输速度(千米/小时)
运输费用(元/千米)
装卸时间(小时)
装卸费用(元)
甲公司
60
6
4
1600
乙公司
a
8
b
1000
现已知乙公司的运输速度比甲公司的运输速度慢10千米/小时,但装卸时间比甲公司少2小时,两家运输公司的运输及装卸的费用总和相等.
(1)填空:a=
,b=
.
(2)求A、B两地之间的路程;
(3)若这批不易存放的水果在运输与装卸的过程中的损耗为300元/小时,请你算出果品公司选择这两家公司所需的总费用(运输费、装卸费、损耗费三项之和)分别是多少元,并指出从经济角度应选择哪一家公司.
3.缴纳个人所得税是收入达到缴纳标准的公民应居的义务,个人所得税率是由国家相应的法律法规规定的.根据个人的收入计算,新修改的《中华人民共和国个人所得税法》于2019年1月1日正式实施,新税法规定个人所得税的免征额为5000元,应纳税所得额按如下税率表缴纳个人所得税(应纳税所得额=税前收总额﹣国家规定扣除专项金额﹣免征额).
级数
应纳税所得额
税率%
1
不超过3000元的
3
2
超过3000元至12000元的部分
10
3
超过12000元至25000元的部分
20
…
…
…
根据以上信息,解决以下问题:
(1)小明的妈妈应纳税所得额为2000元,她应该缴纳个人所得税
元.
(2)小明的爸爸要缴纳个人所得税590元,他应纳税所得额是多少元?
(3)如果小明的爸爸和妈妈某月应纳税所得额共为20000元(爸爸的应纳税所得额高于妈妈的应纳税所得额),共要缴纳个人所得税1780元,小明的爸爸应纳税所得额是
元.
4.某市为了鼓励居民节约用水,采用分阶段计费的方法按月计算每户家庭的水费:月用水量不超过20m2时,按2元/m2计算:月用水量超过20m2时,其中的20m2仍按2元/m2计算,超过部分按2.6元/m2计算.设某户家庭月用水量xm2
(1)用含x的式子表示:
当0≤x≤20时,水费为
元;当x>20时,水费为
元;
(2)
月份
4月
5月
6月
用水量
15
17
a
小花家第二季度用水情况如上表,小花家这个季度共缴纳水费117元,请你求出小花家6月份用水量a的值?
5.下表是中国电信两种“4G套餐”计费方式.(月基本费固定收,主叫不超过主叫时间,流量不超上网流量不再收取额外费用,主叫超时和上网超流量部分加收超时费和超流量费)
月基本费/元
主叫通话/分钟
上网流量/MB
接听
主叫超时(元/分钟)
超出流量(元/MB)
套餐1
49
200
500
免费
0.20
0.3
套餐2
69
250
600
免费
0.15
0.2
(1)6月小王主叫通话时间220分钟,上网流量800MB.按套餐1计费需
元,按套餐2计费需
元;若他按套餐2计费需129元,主叫通话时间为240分钟,则他上网使用了
MB流量;
(2)若上网流量为540MB,是否存在某主叫通话时间t(分钟),按套餐1和套餐2的计费相等?若存在,请求出t的值;若不存在,请说明理由.
6.近期电影《少年的你》受到广大青少年的喜爱,某校七年级1班、2班的几名同学请他们的家长在网上买票,家长了解到某电影院的活动,设购买电影票的张数为n:
购买张数
1≤n≤50
51≤n≤100
n>100
每张票的价格
38元
30元
26元
家长沟通后决定两个班的同学在期中考试结束后去观看.两个班共有104人,其中1班人数多于40不足50人.经过估算,如果两个班都以班为单位购买,则一共应付3504元.
(1)求两个班各有多少同学?
(2)如果两个班联合起来,作为一个团体购票,可以节省多少钱?
(3)如果七年级1班同学作为一个团体购票,你认为如何购票才最省钱?可以节省多少钱?
7.阅读材料:为落实水资源管理制度,大力促进水资源节约,本市居民用水实行阶梯水价,按年度用水量计算,将居民家庭全年用水量划分为三档,水价分档递增,实施细则如表:
北京市居民用水阶梯水价表
(单位:元/立方米)
供水类型
阶梯
户年用水量(立方米)
水价
自来水
第一阶梯
0﹣150(含)
5
第二阶梯
151﹣260(含)
7
第三阶梯
260以上
9
如某居民去年用水量为160立方米,则其应缴纳水费为150×5+(160﹣150)×7=820元.
(1)若小明家去年用水量为100立方米,则小明家应缴纳的水费为
元;
(2)若小明家全年用水x立方米,且总量不超过240立方米,则应缴纳的水费为
元?(用含x的代数式表示);
(3)若小明家今年全年共纳水费925元,则小明家共用水多少立方米?
8.某市居民使用自来水按如下标准收费(水费按月缴纳)
户月用水量
单价
不超过12m3的部分
2元/m3
超过12m3但不超过20m3的部分
3元/m3
超过20m3的部分
4元/m3
(1)某用户一个月用了14m3水,求该用户这个月应缴纳的水费
(2)某户月用水量为n立方米(12<n≤20),该用户缴纳的水费是39元,列方程求n的值
(3)甲、乙两用户一个月共用水40m3,设甲用户用水量为xm3,且12<x≤28
①当12<x≤20时,甲、乙两用户一个月共缴纳的水费为
元(用含x的整式表示)
②当20<x≤28时,甲、乙两用户一个月共缴纳的水费为
元(用含x的整式表示)
9.为充分发挥市场机制和价格杠杆在水资源配置中的作用,促进节约用水,提高用水效率,
7月1日起某地实行阶梯水价,价目如表(注:水费按月结算,m3表示立方米):
价目表
每月用水量
单价(元/m3)
不超过18的部分
3
超出18不超出25的部分
4
超出25的部分
7
例:某户居民5月份共用水23m3,则应缴水费3×18+4×(23﹣18)=74(元).
(1)若A居民家1月份共用水12m3,则应缴水费
元;
(2)若B居民家2月份共缴水费66元,则用水
m3;
(3)若C居民家3月份用水量为am3(a低于20m3,即a<20),且C居民家3、4两个月用水量共40m3,求3、4两个月共缴水费多少元?(用含a的代数式表示,不要求化简)
(4)在(3)中,当a=19时,求C居民家3、4两个月共缴水费多少元?
10.某市出租车收费标准如下表所示,根据此收费标准,解决下列问题:
行驶路程
收费标准
不超出3km的部分
起步价7元+燃油附加费1元
超出3km不超出6km的部分
1.6元/km
超出6km的部分
2.4元/km
(1)若行驶路程为5km,则打车费用为
元;
(2)若行驶路程为xkm(x>6),则打车费用为
元(用含x的代数式表示);
(3)当打车费用为32元时,行驶路程为多少千米?
参考答案
1.解:(1)1240﹣104×9=304,
∴可省304元钱;
(2)设七(1)班有x人,
则有13x+11(104﹣x)=1240或13x+9(104﹣x)=1240,
解得:x=48或x=76(不合题意,舍去).
即七(1)班48人,七(2)班56人;
(3)要想享受优惠,由(1)可知七(1)班48人,只需多买3张,
51×11=561,48×13=624>561
∴48人买51人的票可以更省钱.
2.解:(1)依题意,得:60﹣a=10,4﹣b=2,
解得:a=50,b=2.
故答案为:50;2.
(2)设A、B两地之间的路程为s千米,
依题意,得:6s+1600=8s+1000,
解得:s=300.
答:A、B两地之间的路程为300千米.
(3)选择甲公司所需的总费用为300×6+1600+300×(300÷60+4)=6100(元),
选择乙公司所需的总费用为300×8+1000+300×(300÷50+4)=6400(元).
∵6100<6400,
∴选择甲公司总费用更少.
3.解:(1)由题意知,2000×3%=60(元)
故答案是:60;
(2)易知:小明爸爸在第2级中的税,设他的应纳税所得额为a元,则
90+(a﹣3000)×10%=590.
解得a=8000.
∴小明爸爸应纳税所得额为8000元
(3)设小明的爸爸应纳税所得额是x元,则小明的妈妈应纳税所得额是(20000﹣x)元,则10000<x<20000
①当10000<x<12000时,则90+(x﹣3000)×10%+90+(20000﹣x﹣3000)×10%=1780,无解,舍去;
②当12000<x<17000时,则90+(12000﹣3000)×10%+(x﹣12000)×20%+90+(20000﹣x﹣3000)×10%=1780.
解得x=14000.
③当17000<x<20000时,则90+(12000﹣3000)×10%+(x﹣12000)×20%+(20000﹣x)×3%=1780.
解得x=,舍去.
综上所述,小明的爸爸应纳税所得额是
14000元.
故答案是:14000.
4.解:(1)当0≤x≤20时,水费为2x元;当x>20时,水费为20×2+2.6(x﹣20)=(2.6x﹣12)元.
故答案为:2x、(2.6x﹣12);
(2)由题意得,小花家4月份,5月份共交水费15×2+17×2=30+34=64(元),则6月份用水量a>20,
∴小花家6月份的用水为a吨,则超过20吨的部分为(a﹣20)吨,
∴15×2+17×2+20×2+2.6(a﹣20)=117,
解得:a=25.
答:小花家6月份用水25吨.
5.解:(1)套餐1:
49+0.2×(220﹣200)+0.3×(800﹣500)
=49+0.2×20+0.3×300
=49+4+90
=143.
套餐2:
69+0.2×(800﹣600)
=69+0.2×200
=69+40
=109.
设上网流量为xMB,则
69+0.2(x﹣600)=129
解得x=900.
故答案为:143;109;900.
(2)当0≤t<200时,
49+0.3×(540﹣500)=61≠69
∴此时不存在这样的t.
当200≤t≤250时,
49+0.2(t﹣200)+0.3×(540﹣500)=69
解得t=240.
当t>250时,
49+0.2(t﹣200)+0.3×(540﹣500)=69+0.15(t﹣250)
解得t=210(舍).
故若上网流量为540MB,当主叫通话时间为240分钟时,按套餐1和套餐2的计费相等.
6.解:(1)设1班有x名同学,则2班有(104﹣x)名学生,
依题意,得:38x+30(104﹣x)=3504,
解得:x=48,
∴104﹣x=56.
答:1班有48名同学,2班有56名学生.
(2)26×104=2704(元),
3504﹣2704=800(元).
答:可以节省800元钱.
(3)购买48张票所需费用为38×48=1824(元),
购买51张票所需费用为30×51=1530(元).
1824>1530,1824﹣1530=294(元).
答:购买51张门票最省钱,可以节省294元钱.
7.解:(1)100×5=500(元).
故答案为:500.
(2)当0<x≤150时,应缴纳水费为5x元;
当150<x≤240时,应缴纳水费为150×5+(x﹣150)×7=(7x﹣300)元.
故答案为:.
(3)150×5=750(元),150×5+(260﹣150)×7=1520(元).
∵750<925<1520,
∴150<x<260.
依题意,得:7x﹣300=925,
解得:x=175.
答:小明家共用水175立方米.
8.解:(1)由题意可得:2×12+3×(14﹣12)=30元,
答:该用户这个月应缴纳30元水费.
(2)由题意可得,2×12+3(n﹣12)=39,
解得n=17;
(3)①∵12<x≤20,
∴乙用户用水量20≤40﹣x<28,
∴12×2+3(x﹣12)+12×2+3×8+4(40﹣x﹣20)=(116﹣x)元;
②∵20<x≤28,
∴乙用户用水量12≤40﹣x<20,
∴12×2+3×8+4(x﹣20)+12×2+3(40﹣x﹣12)=(x+76)元;
故答案为(116﹣x)元,(x+76)元.
9.解:(1)∵12<18,
∴应缴水费12×3=36(元),
故答案为:36;
(2)设B居民家2月份用水xm3,
∴3×18+4×(x﹣18)=66,
解得x=21.
故答案为:21.
(3)①当a<15时,4月份的用水量超过25m3
共缴水费:3a+3×18+4(25﹣18)+7(40﹣a﹣25)=187﹣4a,
②当15≤a≤18时,4月份的用水量不低于22m3且不超过25m3
共缴水费:3a+3×18+4(40﹣a﹣18)=142﹣a,
③当18<a≤20时,4月份的用水量超过20m3且不超过22m3
共缴水费:3×18+4(a﹣18)+3×18+4(40﹣a﹣18)=124,
(4)当a=19时,C居民家3、4两个月共缴水费124元.
10.解:(1)支付车费:7+1+(5﹣3)×1.6=11.2(元),
故答案为:11.2;
(2)7+1+1.6×3+2.4(x﹣6)
=8+4.8+2.4x﹣14.4
=2.4x﹣1.6(元),
故答案为:(2.4x﹣1.6);
(3)设当打车费用为32元时,行驶路程为x千米,
由题意得:2.4x﹣1.6=32,
解得:x=14,
∴当打车费用为32元时,行驶路程为14千米.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
