7.1 为什么要证明 课件(共40张PPT)
文档属性
| 名称 | 7.1 为什么要证明 课件(共40张PPT) | 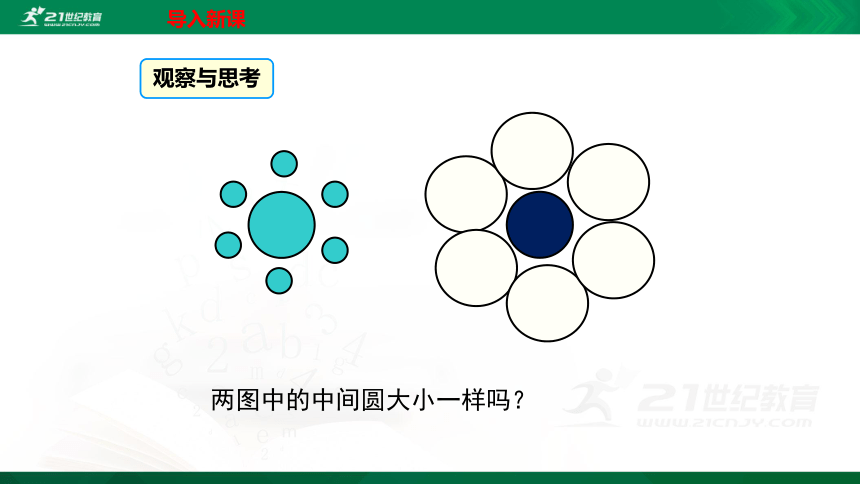 | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 10:02:06 | ||
图片预览











文档简介
导入新课
观察与思考
两图中的中间圆大小一样吗?
这两个色块颜色有什么不同?旋转再看看
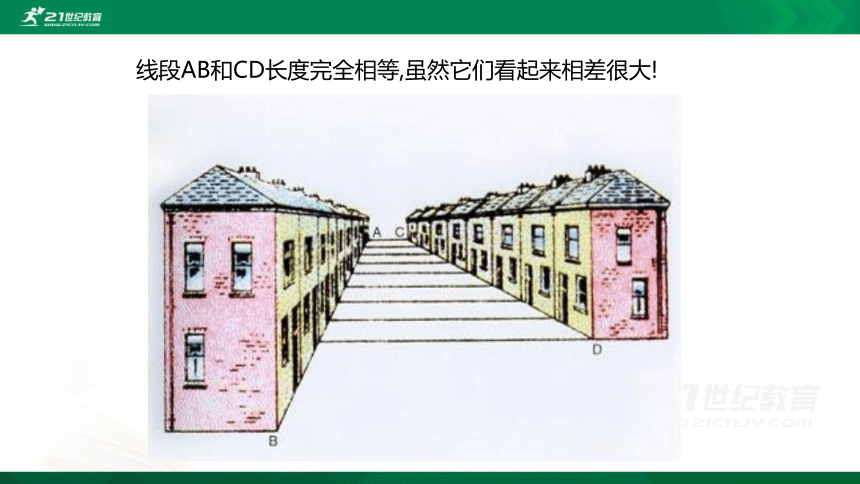
线段AB和CD长度完全相等,虽然它们看起来相差很大!
是静还是动?
平行线:不敢相信图中的横线是平行的,不过它们就是平行线!
你觉得观察得到的结论正确吗?
7.1 为什么要证明
学习目标
1.了解推理的意义,知道要判断一个数学结论是否正确,必须进行推理.(重点)
2.会用实验验证、举出反例、推理等方法简单地验证一个数学结论是否正确.(难点)
新知导入
同学们,请你们用学过的数学知识解决下面的问题。
从A地到B地有五条道路,时间紧急,张先生要从B地赶往A地乘车,此时张先生应该选择哪条路?
张先生应该走第③条路.
你的依据是什么?
两点之间,线段最短.
你还记得我们是如何得到“两点之间,线段最短”这个结论的吗?
新知导入
我们曾经通过观察、实验、归纳等活动得到了很多正确的结论.
但是通过观察、实验、归纳得到的结论一定正确吗?
如何才能得到正确的结论呢?
新知导入
图(1)中的两条线段a,b长度相等吗?
观察的结果是线段a比较长;
经过测量,线段a,b长度相等.
新知导入
图(2)中的四边形是正方形吗?
请你先观察,再设法检验你观察到的结论.
观察的结果是四边形的四条边是曲线;
经过直尺验证,四边形是正方形.
新知讲解
如图,把地球看成球形,假设用一根比地球赤道长1米的铁丝将地球赤道围起来,铁丝与地球赤道之间的间隙能有多大?能放进一个拳头吗?先凭感觉想象一下,再具体算一算,看看与你的感觉是否一致,并与同伴进行交流.
解:设赤道的周长为C米,则铁丝的长为(C+1)米,那么铁丝与地球赤道间的间隙为R-r,
0.16 m=16 cm.
新知讲解
通过计算我们可以看出,判断一个结论是否正确,依靠直觉是不可靠的.要想得到正确的结论,必须经过计算来证实.
请大家解决下面问题.
代数式n2-n+11的值是质数吗?取n=0,1,2,3,4,5试一试,你能否由此得到结论:对于所有自然数n,n2-n+11的值都是质数?与同伴进行交流.
讲授新课
判断一个数学结论是否正确,仅观察、猜想、
实验还不够;
必须经过一步一步、 有根有据的推理.
请举例说明,你用到过的推理.
一、数学的结论必须经过严格的论证
a
b
考考你的眼力
线段a与线段b哪个
比较长?
a
b
c
d
谁与线段d在
一条直线上?
a
b
a
b
c
d
检验你的结论
a=b
做一做
如图,假如用一根比地球的赤道长1米的铁丝将地球赤道围起来,那么铁丝与地球赤道之间的间隙能有多大?(地球看成球形)能放进一个红枣吗?能放进一个拳头吗?
解:设赤道周长为c,铁丝与地球赤道
之间的间隙为 :
它们的间隙不仅能放进一个红枣,而且也能放进一个拳头.
费 马
对于所有自然数n, 的值都是质数.
当n=0,1,2,3,4时,
= 3,5,17,257,65 537
都是质数
欧 拉
当n=5时,
= 4 294 967 297=
641×6 700 417
举出反例是检验错误数学结论的有效方法.
大数学家也有失误
归纳总结
这个故事告诉我们:
1. 学习欧拉的求实精神与严谨的科学态度.
2.没有严格的推理,仅由若干特例归纳、猜测的结论可能潜藏着错误,未必正确.
3.要证明一个结论是错误的,举反例就是一种常用方法.
【类型一】 实验验证
例1:先观察再验证.
(1)图①中实线是直的还是弯曲的?
(2)图②中两条线段a与b哪一条更长?
(3)图③中的直线AB与直线CD平行吗?
二、检验数学结论的常用方法
解:观察可能得出的结论是:
(1)实线是弯曲的;
(2)a更长一些;
(3)AB与DC不平行.
而我们用科学的方法验证后发现:
(1)实线是直的;
(2)a与b一样长;
(3)AB平行于CD.
方法归纳
有时视觉受周围环境的影响,往往误导我们,让我们得出错误的结论,所以仅靠经验、观察是不够的,只有通过科学的实验进行严格的推理,才能得出最准确的结论.
【类型二】 推理证明
例2:当n为正整数时,代数式(n2-5n+5)2的值都
等于1吗?
解:当n=1时,(n2-5n+5)2=12=1;
当n=2时,(n2-5n+5)2=(-1)2=1;
当n=3时,(n2-5n+5)2=(-1)2=1;
当n=4时,(n2-5n+5)2=12=1;
当n=5时,(n2-5n+5)2=52=25≠1.
所以当n为正整数时,(n2-5n+5)2不一定等于1.
【方法总结】验证特例是判断一个结论错误的最好方法.
【类型三】 举出反例
例3:如图,从点O出发作出四条射线OA、OB、OC、OD,已知OA⊥OC,OB⊥OD.
(1)若∠BOC=30°,求∠AOB和∠COD的度数;
(2)若∠BOC=54°,求∠AOB和∠COD的度数;
(3)由(1)、(2)你发现了什么?
(4)你能肯定上述的发现吗?
分析:图中∠AOB、∠COD均与∠BOC互余,根据角的和、差关系,可求得∠AOB与∠COD的度数.通过计算发现∠AOB=∠COD,于是可以归纳∠AOB=∠COD.
例3:如图,从点O出发作出四条射线OA、OB、OC、OD,已知OA⊥OC,OB⊥OD.
(1)若∠BOC=30°,求∠AOB和∠COD的度数;
解:(1)∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°.
∵∠BOC=30°,
∴∠AOB=∠AOC-∠BOC=90°-30°=60°,
∠COD=∠BOD-∠BOC=90°-30°=60°.
解:(2)∠AOB=∠AOC-∠BOC=90°-54°=36°,
∠COD=∠BOD-∠BOC=90°-54°=36°.
例3:如图,从点O出发作出四条射线OA、OB、OC、OD,已知OA⊥OC,OB⊥OD.
(2)若∠BOC=54°,求∠AOB和∠COD的度数;
解:(4)∵∠AOB+∠BOC=∠AOC=90°,
∠BOC+∠COD=∠BOD=90°,
∴∠AOB+∠BOC=∠BOC+∠COD.
∴∠AOB=∠COD.
【方法总结】检验数学结论具体经历的过程是:观察、度量、实验→猜想归纳→结论→推理→正确结论.
例3:如图,从点O出发作出四条射线OA、OB、OC、OD,已知OA⊥OC,OB⊥OD.
(4)你能肯定上述的发现吗?
课堂练习
1.小刚和小明在手工制作课上,用同种小铁丝制作的楼梯模型如图所示.那么他们用的材料长度( )
A.一样多 B.小刚的多 C.小明的多 D.无法判断
A
课堂练习
2.骑自行车的速度是每小时15千米,骑摩托车的速度是每小时40千米,则下列结论中你能肯定的是 ( )
A.从A地到B地,骑摩托车的人一定比骑自行车的人先到达
B.从A地到B地,骑自行车的人一定比骑摩托车的人先到达
C.从A地到B地,骑自行车的人和骑摩托车的人不可能同时到达
D.从A地到B地,骑自行车的人有可能比骑摩托车的人先到达
D
课堂练习
3.下列说法正确的是 ( )
A.通过观察完全可以判断一个数学结论的正确与否
B.推理是科学家的事,与我们没有多大的关系
C.对于自然数n,n2+n+37一定是质数
D.有10个苹果,将它们放进9个筐中,则至少有一个筐中的苹果数不少于2个
D
课堂练习
4.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示,按照下面的规律,摆第n个图需要火柴棒的根数为 .
6n+2
拓展提高
5.数学家迪布凡尔在1590年曾注意到,在形如6n-1和6n+1的数对5,7;11,13;17,19;23,25;29,31;35,37;41,43;…中,当“n”在取前几个自然数时,都至少有一个质数,由此他提出猜想:“对于任何自然数n(n≠0),6n-1和6n+1这两个数中至少有一个质数.”你认为这个猜想正确吗?
验证一下:n=8时,结论成立吗?n=9呢?n=10呢?n=20呢?
这说明了什么?
拓展提高
解:不正确.
当n=8,9,10时结论都成立,当n=20时结论不成立.
说明观察、归纳和猜想是重要的,但仅凭此得出的结论不一定可信,还必须经过严格的推理证明.
课堂总结
为什么要证明
数学结论必须经过严格的论证
实验验证
举出反例
推理证明
论证方法
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
观察与思考
两图中的中间圆大小一样吗?
这两个色块颜色有什么不同?旋转再看看
线段AB和CD长度完全相等,虽然它们看起来相差很大!
是静还是动?
平行线:不敢相信图中的横线是平行的,不过它们就是平行线!
你觉得观察得到的结论正确吗?
7.1 为什么要证明
学习目标
1.了解推理的意义,知道要判断一个数学结论是否正确,必须进行推理.(重点)
2.会用实验验证、举出反例、推理等方法简单地验证一个数学结论是否正确.(难点)
新知导入
同学们,请你们用学过的数学知识解决下面的问题。
从A地到B地有五条道路,时间紧急,张先生要从B地赶往A地乘车,此时张先生应该选择哪条路?
张先生应该走第③条路.
你的依据是什么?
两点之间,线段最短.
你还记得我们是如何得到“两点之间,线段最短”这个结论的吗?
新知导入
我们曾经通过观察、实验、归纳等活动得到了很多正确的结论.
但是通过观察、实验、归纳得到的结论一定正确吗?
如何才能得到正确的结论呢?
新知导入
图(1)中的两条线段a,b长度相等吗?
观察的结果是线段a比较长;
经过测量,线段a,b长度相等.
新知导入
图(2)中的四边形是正方形吗?
请你先观察,再设法检验你观察到的结论.
观察的结果是四边形的四条边是曲线;
经过直尺验证,四边形是正方形.
新知讲解
如图,把地球看成球形,假设用一根比地球赤道长1米的铁丝将地球赤道围起来,铁丝与地球赤道之间的间隙能有多大?能放进一个拳头吗?先凭感觉想象一下,再具体算一算,看看与你的感觉是否一致,并与同伴进行交流.
解:设赤道的周长为C米,则铁丝的长为(C+1)米,那么铁丝与地球赤道间的间隙为R-r,
0.16 m=16 cm.
新知讲解
通过计算我们可以看出,判断一个结论是否正确,依靠直觉是不可靠的.要想得到正确的结论,必须经过计算来证实.
请大家解决下面问题.
代数式n2-n+11的值是质数吗?取n=0,1,2,3,4,5试一试,你能否由此得到结论:对于所有自然数n,n2-n+11的值都是质数?与同伴进行交流.
讲授新课
判断一个数学结论是否正确,仅观察、猜想、
实验还不够;
必须经过一步一步、 有根有据的推理.
请举例说明,你用到过的推理.
一、数学的结论必须经过严格的论证
a
b
考考你的眼力
线段a与线段b哪个
比较长?
a
b
c
d
谁与线段d在
一条直线上?
a
b
a
b
c
d
检验你的结论
a=b
做一做
如图,假如用一根比地球的赤道长1米的铁丝将地球赤道围起来,那么铁丝与地球赤道之间的间隙能有多大?(地球看成球形)能放进一个红枣吗?能放进一个拳头吗?
解:设赤道周长为c,铁丝与地球赤道
之间的间隙为 :
它们的间隙不仅能放进一个红枣,而且也能放进一个拳头.
费 马
对于所有自然数n, 的值都是质数.
当n=0,1,2,3,4时,
= 3,5,17,257,65 537
都是质数
欧 拉
当n=5时,
= 4 294 967 297=
641×6 700 417
举出反例是检验错误数学结论的有效方法.
大数学家也有失误
归纳总结
这个故事告诉我们:
1. 学习欧拉的求实精神与严谨的科学态度.
2.没有严格的推理,仅由若干特例归纳、猜测的结论可能潜藏着错误,未必正确.
3.要证明一个结论是错误的,举反例就是一种常用方法.
【类型一】 实验验证
例1:先观察再验证.
(1)图①中实线是直的还是弯曲的?
(2)图②中两条线段a与b哪一条更长?
(3)图③中的直线AB与直线CD平行吗?
二、检验数学结论的常用方法
解:观察可能得出的结论是:
(1)实线是弯曲的;
(2)a更长一些;
(3)AB与DC不平行.
而我们用科学的方法验证后发现:
(1)实线是直的;
(2)a与b一样长;
(3)AB平行于CD.
方法归纳
有时视觉受周围环境的影响,往往误导我们,让我们得出错误的结论,所以仅靠经验、观察是不够的,只有通过科学的实验进行严格的推理,才能得出最准确的结论.
【类型二】 推理证明
例2:当n为正整数时,代数式(n2-5n+5)2的值都
等于1吗?
解:当n=1时,(n2-5n+5)2=12=1;
当n=2时,(n2-5n+5)2=(-1)2=1;
当n=3时,(n2-5n+5)2=(-1)2=1;
当n=4时,(n2-5n+5)2=12=1;
当n=5时,(n2-5n+5)2=52=25≠1.
所以当n为正整数时,(n2-5n+5)2不一定等于1.
【方法总结】验证特例是判断一个结论错误的最好方法.
【类型三】 举出反例
例3:如图,从点O出发作出四条射线OA、OB、OC、OD,已知OA⊥OC,OB⊥OD.
(1)若∠BOC=30°,求∠AOB和∠COD的度数;
(2)若∠BOC=54°,求∠AOB和∠COD的度数;
(3)由(1)、(2)你发现了什么?
(4)你能肯定上述的发现吗?
分析:图中∠AOB、∠COD均与∠BOC互余,根据角的和、差关系,可求得∠AOB与∠COD的度数.通过计算发现∠AOB=∠COD,于是可以归纳∠AOB=∠COD.
例3:如图,从点O出发作出四条射线OA、OB、OC、OD,已知OA⊥OC,OB⊥OD.
(1)若∠BOC=30°,求∠AOB和∠COD的度数;
解:(1)∵OA⊥OC,OB⊥OD,
∴∠AOC=∠BOD=90°.
∵∠BOC=30°,
∴∠AOB=∠AOC-∠BOC=90°-30°=60°,
∠COD=∠BOD-∠BOC=90°-30°=60°.
解:(2)∠AOB=∠AOC-∠BOC=90°-54°=36°,
∠COD=∠BOD-∠BOC=90°-54°=36°.
例3:如图,从点O出发作出四条射线OA、OB、OC、OD,已知OA⊥OC,OB⊥OD.
(2)若∠BOC=54°,求∠AOB和∠COD的度数;
解:(4)∵∠AOB+∠BOC=∠AOC=90°,
∠BOC+∠COD=∠BOD=90°,
∴∠AOB+∠BOC=∠BOC+∠COD.
∴∠AOB=∠COD.
【方法总结】检验数学结论具体经历的过程是:观察、度量、实验→猜想归纳→结论→推理→正确结论.
例3:如图,从点O出发作出四条射线OA、OB、OC、OD,已知OA⊥OC,OB⊥OD.
(4)你能肯定上述的发现吗?
课堂练习
1.小刚和小明在手工制作课上,用同种小铁丝制作的楼梯模型如图所示.那么他们用的材料长度( )
A.一样多 B.小刚的多 C.小明的多 D.无法判断
A
课堂练习
2.骑自行车的速度是每小时15千米,骑摩托车的速度是每小时40千米,则下列结论中你能肯定的是 ( )
A.从A地到B地,骑摩托车的人一定比骑自行车的人先到达
B.从A地到B地,骑自行车的人一定比骑摩托车的人先到达
C.从A地到B地,骑自行车的人和骑摩托车的人不可能同时到达
D.从A地到B地,骑自行车的人有可能比骑摩托车的人先到达
D
课堂练习
3.下列说法正确的是 ( )
A.通过观察完全可以判断一个数学结论的正确与否
B.推理是科学家的事,与我们没有多大的关系
C.对于自然数n,n2+n+37一定是质数
D.有10个苹果,将它们放进9个筐中,则至少有一个筐中的苹果数不少于2个
D
课堂练习
4.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示,按照下面的规律,摆第n个图需要火柴棒的根数为 .
6n+2
拓展提高
5.数学家迪布凡尔在1590年曾注意到,在形如6n-1和6n+1的数对5,7;11,13;17,19;23,25;29,31;35,37;41,43;…中,当“n”在取前几个自然数时,都至少有一个质数,由此他提出猜想:“对于任何自然数n(n≠0),6n-1和6n+1这两个数中至少有一个质数.”你认为这个猜想正确吗?
验证一下:n=8时,结论成立吗?n=9呢?n=10呢?n=20呢?
这说明了什么?
拓展提高
解:不正确.
当n=8,9,10时结论都成立,当n=20时结论不成立.
说明观察、归纳和猜想是重要的,但仅凭此得出的结论不一定可信,还必须经过严格的推理证明.
课堂总结
为什么要证明
数学结论必须经过严格的论证
实验验证
举出反例
推理证明
论证方法
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
