人教版八年级数学下册课件:18.1.1平行四边形的性质课时2(共27张ppt)
文档属性
| 名称 | 人教版八年级数学下册课件:18.1.1平行四边形的性质课时2(共27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 529.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 13:30:26 | ||
图片预览





文档简介
(共27张PPT)
18.1.1
平行四边形的性质
课时2
知识回顾
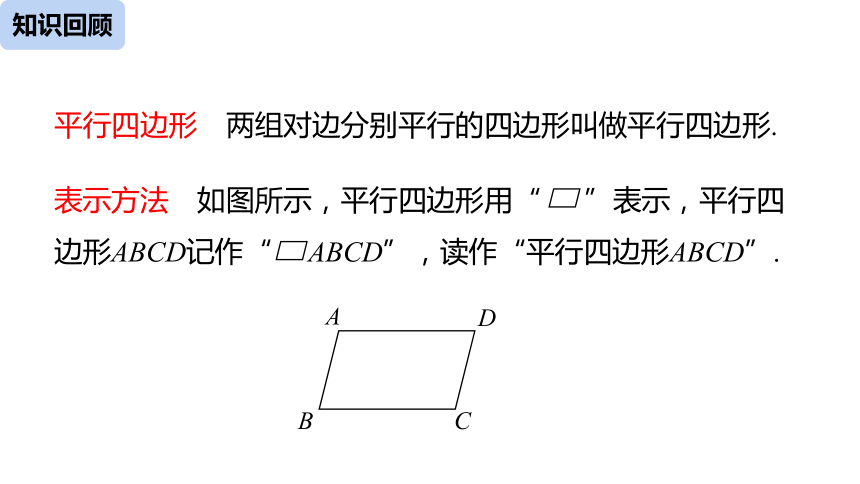
平行四边形
两组对边分别平行的四边形叫做平行四边形.
表示方法
如图所示,平行四边形用“
”表示,平行四边形ABCD记作“
ABCD”,读作“平行四边形ABCD”.
A
B
C
D
A
B
C
D
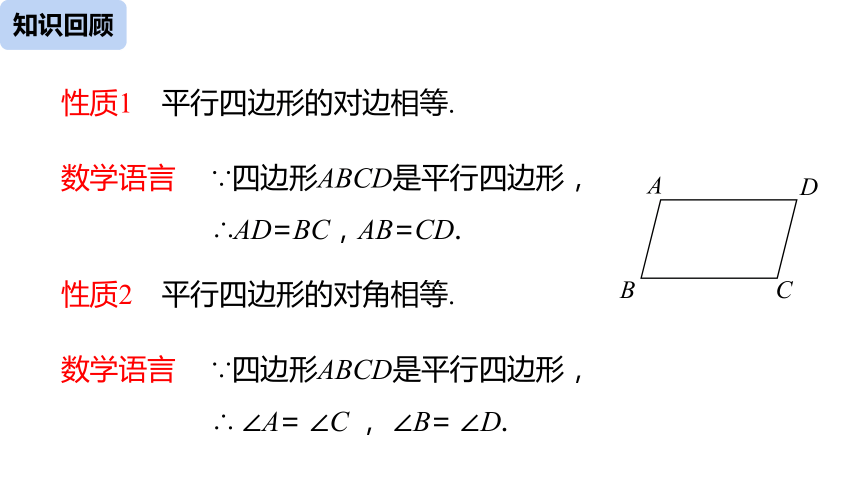
性质1
平行四边形的对边相等.
数学语言
∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD.
知识回顾
性质2
平行四边形的对角相等.
数学语言
∵四边形ABCD是平行四边形,
∴
∠A=
∠C
,
∠B=
∠D.
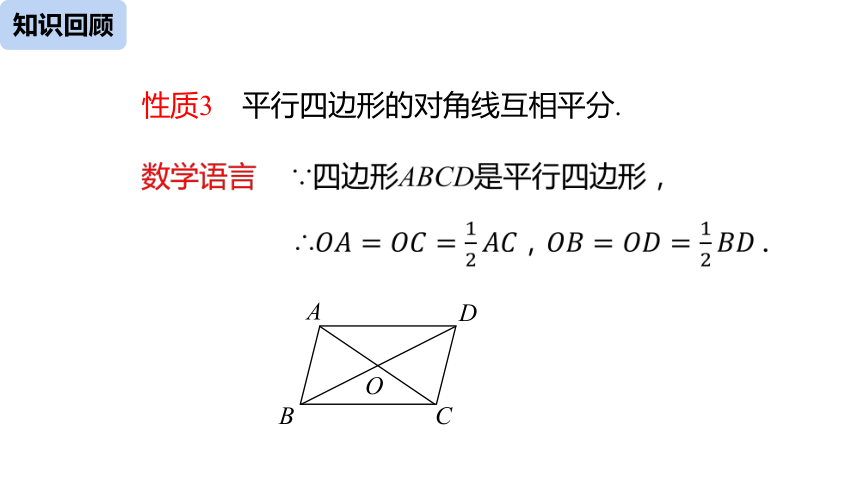
性质3
平行四边形的对角线互相平分.
?
A
B
C
D
O
知识回顾
知识回顾
●
●
两点间的距离:连结两点的线段的长度.
点到直线的距离:从直线外一点到这条直线的垂线段的长度.
●
┐
学习目标
1.理解两条平行线之间的距离的概念.
2.能熟练运用平行线之间的距离的概念去解题.
课堂导入
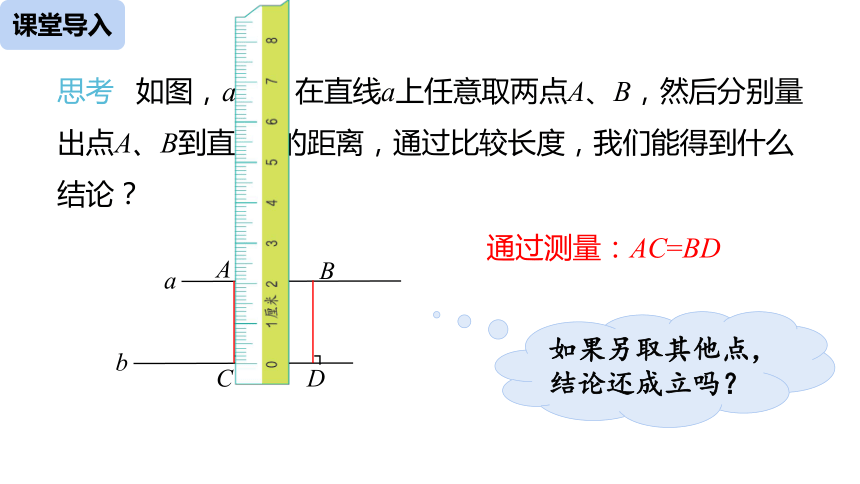
思考
如图,a//b,在直线a上任意取两点A、B,然后分别量出点A、B到直线b的距离,通过比较长度,我们能得到什么结论?
通过测量:AC=BD
a
b
A
B
┐
┐
C
D
如果另取其他点,结论还成立吗?
新知探究
知识点:两条平行线之间的距离
两条平行线之间的距离
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
数学语言:a//b,A是a上的任意一点,AB⊥b,B是垂足,
线段AB的长就是a、b之间的距离.
a
b
A
┐
B
新知探究
距离
两点间的距离
点到直线的距离
两条平行线之间的距离
区别
联系
连接两点的线段的长度
点到直线的垂线段的长度
两条平行线中,从一条直线上任一点到另一条直线的垂线段的长度
都是指某一条线段的长度
新知探究
如图,直线l1
//
l2
,A,B是直线
l1上任意两点,AC⊥l2,BD⊥l2,垂足分别为C、D,求证:AC=BD.
证明:∵
AC⊥CD,
BD⊥CD.
∴∠1=∠2=90?
∴
AC//BD
∵
AC//BD
,
AB//CD
∴
四边形ABCD是平行四边形,AC=BD.
l1
l2
A
B
┐
┐
C
D
1
2
新知探究
性质
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
数学语言
如图所示,A、C是直线l1上的任意两点.
l1
l2
A
B
┐
┐
C
D
∵
l1
//
l2
,AB⊥
l2
,CD⊥
l2
,
∴
AB=CD.
思考
如图,a//b,c//d,c、d与a、b分别相交于点A、B、C、D四点,那么由平行四边形的性质,我们能得到什么结论?
a
b
c
d
A
B
C
D
∵
a//b,c
//d
∴
AB
//CD,AD
//BC
∴
四边形ABCD是平行四边形,AB=CD.
新知探究
夹在两条平行线之间的平行线段相等.
新知探究
(1)因为平行线间的距离处处相等,所以在作平行四边形的高时,可根据需要灵活选择位置.
?
1.如图,已知AD//BC,判断S△ABC和S△DBC是否相等,并说明理由.
跟踪训练
A
B
C
D
解:由图可知,△ABC
和△DBC
有一条公共边BC
∵
AD//BC
∴
点D、点A到BC的距离相等
∴
△ABC
和△DBC
同底等高,面积相等.
2.
如图,a//b,AB//CD,FG⊥b,CE⊥b,下列说法不正确的是(
).
跟踪训练
A.AB=CD
B.EC=FG
C.AB=FG
D.a、b之间的距离就是CE的长度
C
A
B
C
D
E
F
G
┐
┐
a
b
1.已知直线a//b,点B、C、D是直线a上的三点,点A是直线b上一点,且AB=8、AC=5、AD=4,则两直线之间的距离(
).
A.等于4
B.小于4
C.不小于4
D.不大于4
b
A
a
C
B
D
B
解析:点A到直线a的距离是点A与直线a上任意一点构成的线段中最短的.
随堂练习
随堂练习
2.如图,直线
AE//BD,点
C
在
BD上,若AE=5,BD=6,三角形ABD的面积为18,则三角形ACE的面积为
.
?
A
B
C
D
E
15
随堂练习
3.设直线a、b、c是三条平行直线,已知a与b的距离为4cm,b与c的距离为6cm,求a与c的距离.
解:因为要考虑c的位置,所以要分情况讨论.
a
c
b
①如图所示:直线c在直线b的右侧时,a与c的距离是6+4=10cm.
随堂练习
3.设直线a、b、c是三条平行直线,已知a与b的距离为4cm,b与c的距离为6cm,求a与c的距离.
a
c
b
②如图所示:直线c在直线a的左侧时,a与c的距离是6-4=2cm.
所以a与c的距离是2cm或10cm.
随堂练习
4.如图所示,a//b,在直线a、b上各取一点A、B,连接AB,过点A可以向直线b作多少条线段?其中垂线段AC的垂足为C,则AC与AB的长度关系是什么?
解:过点A可以向直线b作无数条线段,其中垂线段AC最短,所以ACa
A
b
B
C
课堂小结
两条平行线之间的距离
概念
性质
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
夹在两条平行线之间的平行线段相等.
拓展提升
1.如图,已知a//b,三角形ABC的面积为5,BC=EF,则三角形DEF的面积为(
).
A.4
B.5
C.6
D.7
a
A
b
C
B
D
E
F
B
解:点A和点D到直线b的距离相等,又因为BC=EF,所以三角形ABC的面积和三角形DEF的面积相等.
2.如图,在Rt△ABC中,∠B=90?,AB=4
,
BC
>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是
.
解析:因为四边形ABCD是平行四边形,所以AE//CD.由平行线间的距离处处相等,且垂线段最短可知,当DE⊥BC时,DE的值最小,此时DE=AB=4.
4
拓展提升
拓展提升
3.把直线
a
沿着水平方向平移4
cm,平移后的图形为直线
b,则直线
a
与直线
b
之间的距离(
).
A.等于4
cm
B.小于4
cm
C.大于4
cm
D.小于或等于4
cm
本题易出现两方面的错误:(1)只考虑到直线与水平方向垂直的情况;(2)混淆平移距离与平行线间的距离这两个概念.
拓展提升
┐
┐
a
b
4
cm
(1)当直线
a
与水平方向垂直时,直线
a
与直线
b
之间的距离为4
cm.
分两种情况:
拓展提升
(2)当直线
a
与水平方向不垂直时,直线
a
与直线
b之间的距离小于4
cm.
a
b
4
cm
┐
课后作业
请完成课本后习题第2、3题。
18.1.1
平行四边形的性质
课时2
知识回顾
平行四边形
两组对边分别平行的四边形叫做平行四边形.
表示方法
如图所示,平行四边形用“
”表示,平行四边形ABCD记作“
ABCD”,读作“平行四边形ABCD”.
A
B
C
D
A
B
C
D
性质1
平行四边形的对边相等.
数学语言
∵四边形ABCD是平行四边形,
∴AD=BC,AB=CD.
知识回顾
性质2
平行四边形的对角相等.
数学语言
∵四边形ABCD是平行四边形,
∴
∠A=
∠C
,
∠B=
∠D.
性质3
平行四边形的对角线互相平分.
?
A
B
C
D
O
知识回顾
知识回顾
●
●
两点间的距离:连结两点的线段的长度.
点到直线的距离:从直线外一点到这条直线的垂线段的长度.
●
┐
学习目标
1.理解两条平行线之间的距离的概念.
2.能熟练运用平行线之间的距离的概念去解题.
课堂导入
思考
如图,a//b,在直线a上任意取两点A、B,然后分别量出点A、B到直线b的距离,通过比较长度,我们能得到什么结论?
通过测量:AC=BD
a
b
A
B
┐
┐
C
D
如果另取其他点,结论还成立吗?
新知探究
知识点:两条平行线之间的距离
两条平行线之间的距离
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
数学语言:a//b,A是a上的任意一点,AB⊥b,B是垂足,
线段AB的长就是a、b之间的距离.
a
b
A
┐
B
新知探究
距离
两点间的距离
点到直线的距离
两条平行线之间的距离
区别
联系
连接两点的线段的长度
点到直线的垂线段的长度
两条平行线中,从一条直线上任一点到另一条直线的垂线段的长度
都是指某一条线段的长度
新知探究
如图,直线l1
//
l2
,A,B是直线
l1上任意两点,AC⊥l2,BD⊥l2,垂足分别为C、D,求证:AC=BD.
证明:∵
AC⊥CD,
BD⊥CD.
∴∠1=∠2=90?
∴
AC//BD
∵
AC//BD
,
AB//CD
∴
四边形ABCD是平行四边形,AC=BD.
l1
l2
A
B
┐
┐
C
D
1
2
新知探究
性质
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
数学语言
如图所示,A、C是直线l1上的任意两点.
l1
l2
A
B
┐
┐
C
D
∵
l1
//
l2
,AB⊥
l2
,CD⊥
l2
,
∴
AB=CD.
思考
如图,a//b,c//d,c、d与a、b分别相交于点A、B、C、D四点,那么由平行四边形的性质,我们能得到什么结论?
a
b
c
d
A
B
C
D
∵
a//b,c
//d
∴
AB
//CD,AD
//BC
∴
四边形ABCD是平行四边形,AB=CD.
新知探究
夹在两条平行线之间的平行线段相等.
新知探究
(1)因为平行线间的距离处处相等,所以在作平行四边形的高时,可根据需要灵活选择位置.
?
1.如图,已知AD//BC,判断S△ABC和S△DBC是否相等,并说明理由.
跟踪训练
A
B
C
D
解:由图可知,△ABC
和△DBC
有一条公共边BC
∵
AD//BC
∴
点D、点A到BC的距离相等
∴
△ABC
和△DBC
同底等高,面积相等.
2.
如图,a//b,AB//CD,FG⊥b,CE⊥b,下列说法不正确的是(
).
跟踪训练
A.AB=CD
B.EC=FG
C.AB=FG
D.a、b之间的距离就是CE的长度
C
A
B
C
D
E
F
G
┐
┐
a
b
1.已知直线a//b,点B、C、D是直线a上的三点,点A是直线b上一点,且AB=8、AC=5、AD=4,则两直线之间的距离(
).
A.等于4
B.小于4
C.不小于4
D.不大于4
b
A
a
C
B
D
B
解析:点A到直线a的距离是点A与直线a上任意一点构成的线段中最短的.
随堂练习
随堂练习
2.如图,直线
AE//BD,点
C
在
BD上,若AE=5,BD=6,三角形ABD的面积为18,则三角形ACE的面积为
.
?
A
B
C
D
E
15
随堂练习
3.设直线a、b、c是三条平行直线,已知a与b的距离为4cm,b与c的距离为6cm,求a与c的距离.
解:因为要考虑c的位置,所以要分情况讨论.
a
c
b
①如图所示:直线c在直线b的右侧时,a与c的距离是6+4=10cm.
随堂练习
3.设直线a、b、c是三条平行直线,已知a与b的距离为4cm,b与c的距离为6cm,求a与c的距离.
a
c
b
②如图所示:直线c在直线a的左侧时,a与c的距离是6-4=2cm.
所以a与c的距离是2cm或10cm.
随堂练习
4.如图所示,a//b,在直线a、b上各取一点A、B,连接AB,过点A可以向直线b作多少条线段?其中垂线段AC的垂足为C,则AC与AB的长度关系是什么?
解:过点A可以向直线b作无数条线段,其中垂线段AC最短,所以AC
A
b
B
C
课堂小结
两条平行线之间的距离
概念
性质
两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离.
如果两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等,即平行线间的距离处处相等.
夹在两条平行线之间的平行线段相等.
拓展提升
1.如图,已知a//b,三角形ABC的面积为5,BC=EF,则三角形DEF的面积为(
).
A.4
B.5
C.6
D.7
a
A
b
C
B
D
E
F
B
解:点A和点D到直线b的距离相等,又因为BC=EF,所以三角形ABC的面积和三角形DEF的面积相等.
2.如图,在Rt△ABC中,∠B=90?,AB=4
,
BC
>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是
.
解析:因为四边形ABCD是平行四边形,所以AE//CD.由平行线间的距离处处相等,且垂线段最短可知,当DE⊥BC时,DE的值最小,此时DE=AB=4.
4
拓展提升
拓展提升
3.把直线
a
沿着水平方向平移4
cm,平移后的图形为直线
b,则直线
a
与直线
b
之间的距离(
).
A.等于4
cm
B.小于4
cm
C.大于4
cm
D.小于或等于4
cm
本题易出现两方面的错误:(1)只考虑到直线与水平方向垂直的情况;(2)混淆平移距离与平行线间的距离这两个概念.
拓展提升
┐
┐
a
b
4
cm
(1)当直线
a
与水平方向垂直时,直线
a
与直线
b
之间的距离为4
cm.
分两种情况:
拓展提升
(2)当直线
a
与水平方向不垂直时,直线
a
与直线
b之间的距离小于4
cm.
a
b
4
cm
┐
课后作业
请完成课本后习题第2、3题。
