2019--2020学年江苏省八年级上册数学（苏科版）期末考试《勾股定理》试题分类——选择题（Word版 含答案）
文档属性
| 名称 | 2019--2020学年江苏省八年级上册数学（苏科版）期末考试《勾股定理》试题分类——选择题（Word版 含答案） |  | |
| 格式 | zip | ||
| 文件大小 | 151.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 09:51:50 | ||
图片预览
文档简介
2019--2020学年江苏省八年级上册数学（苏科版）期末考试《勾股定理》试题分类——选择题
1．古代数学的“折竹抵地”问题：“今有竹高九尺，末折抵地，去本三尺，问折者高几何？”意思是：现有竹子高9尺，折后竹尖抵地与竹子底部的距离为3尺，问折处高几尺？即：如图，AB+AC＝9尺，BC＝3尺，则AC等于（ ）尺．
A．3.5
B．4
C．4.5
D．5
2．在四条长度分别是1，2，，的线段中，以其中的三条线段长作为边，能组成直角三角形的个数有（ ）
A．0个
B．1个
C．2个
D．3个
3．如图，方格中的点A、B、C、D、E称为“格点”（格线的交点），以这5个格点中的3点为顶点画三角形，可以画等腰三角形和直角三角形的个数分别是（ ）
A．2和3
B．3和3
C．2和4
D．3和4
4．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b．若ab＝6，大正方形的面积为16，则小正方形的面积为（ ）
A．8
B．6
C．4
D．3
5．已知直角三角形两直角边长分别为5，12，则斜边长为（ ）
A．13
B．14
C．15
D．16
6．如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝10，AD＝5，则BD等于（ ）
A．13
B．2
C．8
D．6
7．已知直角三角形的两边长分别为3和4，则斜边长为（ ）
A．4
B．5
C．4或5
D．5或
8．若△ABC中，∠A＝90°，且∠B﹣∠C＝30°，那么∠C的度数为（ ）
A．30°
B．40°
C．50°
D．60°
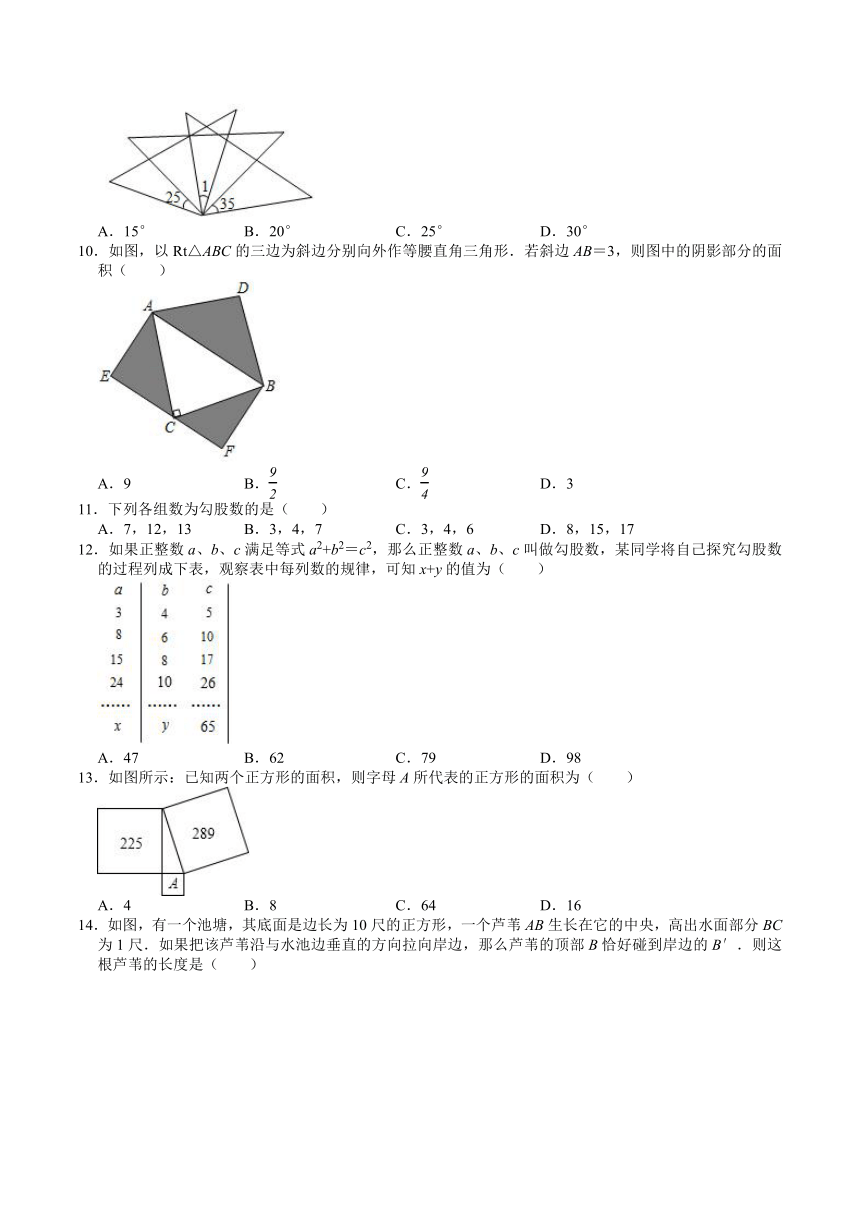
9．如图，若将三个含45°的直角三角板的直角顶点重合放置，则∠1的度数为（ ）
A．15°
B．20°
C．25°
D．30°
10．如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB＝3，则图中的阴影部分的面积（ ）
A．9
B．
C．
D．3
11．下列各组数为勾股数的是（ ）
A．7，12，13
B．3，4，7
C．3，4，6
D．8，15，17
12．如果正整数a、b、c满足等式a2+b2＝c2，那么正整数a、b、c叫做勾股数，某同学将自己探究勾股数的过程列成下表，观察表中每列数的规律，可知x+y的值为（ ）
A．47
B．62
C．79
D．98
13．如图所示：已知两个正方形的面积，则字母A所代表的正方形的面积为（ ）
A．4
B．8
C．64
D．16
14．如图，有一个池塘，其底面是边长为10尺的正方形，一个芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′．则这根芦苇的长度是（ ）
A．10尺
B．11尺
C．12尺
D．13尺
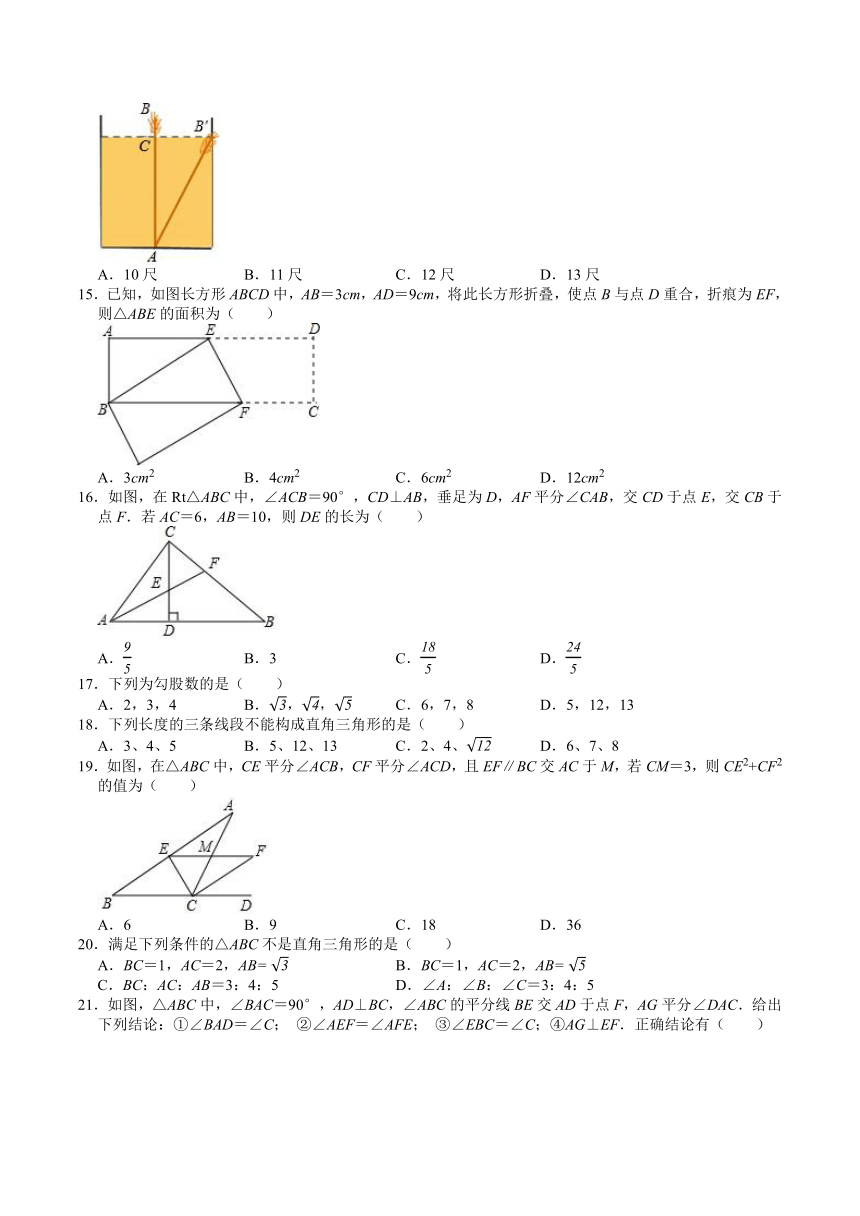
15．已知，如图长方形ABCD中，AB＝3cm，AD＝9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（ ）
A．3cm2
B．4cm2
C．6cm2
D．12cm2
16．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F．若AC＝6，AB＝10，则DE的长为（ ）
A．
B．3
C．
D．
17．下列为勾股数的是（ ）
A．2，3，4
B．，，
C．6，7，8
D．5，12，13
18．下列长度的三条线段不能构成直角三角形的是（ ）
A．3、4、5
B．5、12、13
C．2、4、
D．6、7、8
19．如图，在△ABC中，CE平分∠ACB，CF平分∠ACD，且EF∥BC交AC于M，若CM＝3，则CE2+CF2的值为（ ）
A．6
B．9
C．18
D．36
20．满足下列条件的△ABC不是直角三角形的是（ ）
A．BC＝1，AC＝2，AB
B．BC＝1，AC＝2，AB
C．BC：AC：AB＝3：4：5
D．∠A：∠B：∠C＝3：4：5
21．如图，△ABC中，∠BAC＝90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG平分∠DAC．给出下列结论：①∠BAD＝∠C；
②∠AEF＝∠AFE；
③∠EBC＝∠C；④AG⊥EF．正确结论有（ ）
A．1个
B．2个
C．3个
D．4个
22．在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，下列说法错误的是（ ）
A．如果∠C﹣∠B＝∠A，则△ABC是直角三角形
B．如果c2＝b2﹣a2，则△ABC是直角三角形
C．如果∠A：∠B：∠C＝1：2：3，则△ABC是直角三角形
D．如果a2+b2≠c2，则△ABC不是直角三角形
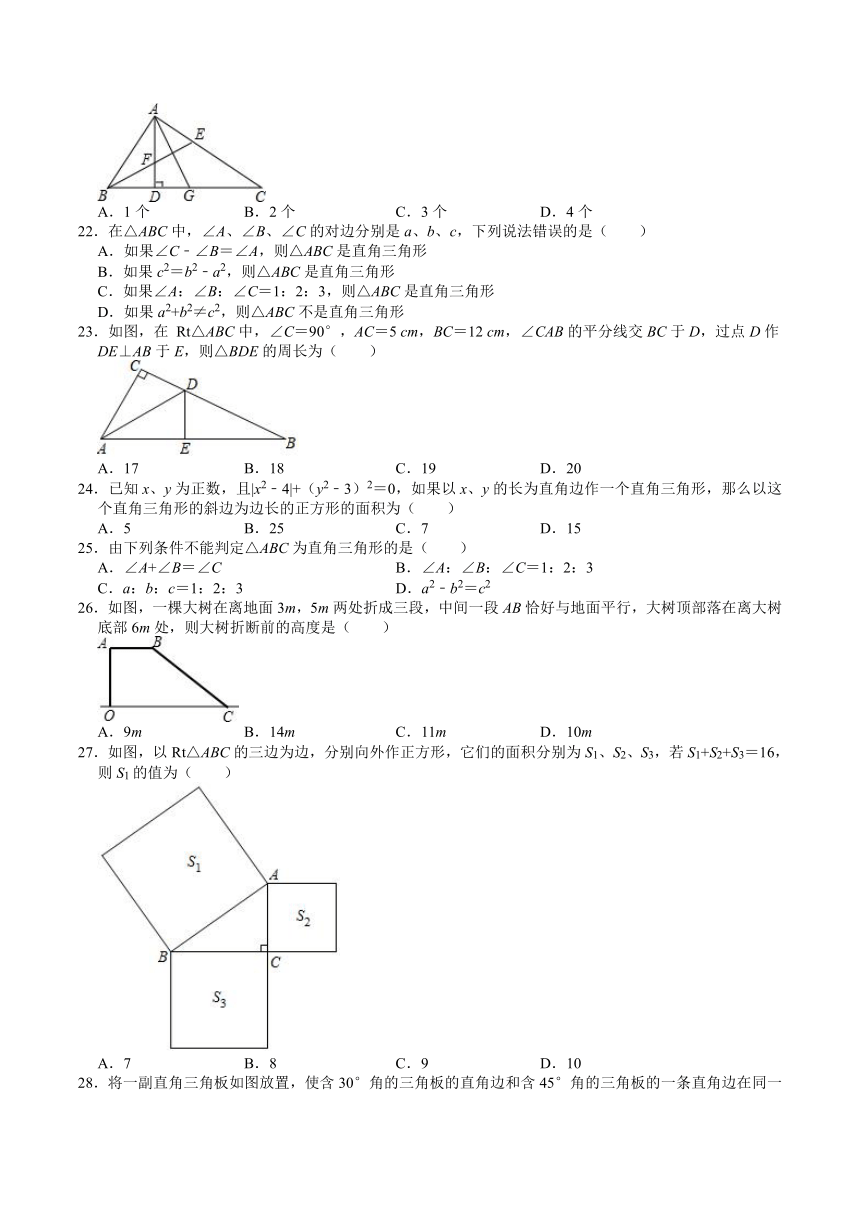
23．如图，在
Rt△ABC中，∠C＝90°，AC＝5
cm，BC＝12
cm，∠CAB的平分线交BC于D，过点D作DE⊥AB于E，则△BDE的周长为（ ）
A．17
B．18
C．19
D．20
24．已知x、y为正数，且|x2﹣4|+（y2﹣3）2＝0，如果以x、y的长为直角边作一个直角三角形，那么以这个直角三角形的斜边为边长的正方形的面积为（ ）
A．5
B．25
C．7
D．15
25．由下列条件不能判定△ABC为直角三角形的是（ ）
A．∠A+∠B＝∠C
B．∠A：∠B：∠C＝1：2：3
C．a：b：c＝1：2：3
D．a2﹣b2＝c2
26．如图，一棵大树在离地面3m，5m两处折成三段，中间一段AB恰好与地面平行，大树顶部落在离大树底部6m处，则大树折断前的高度是（ ）
A．9m
B．14m
C．11m
D．10m
27．如图，以Rt△ABC的三边为边，分别向外作正方形，它们的面积分别为S1、S2、S3，若S1+S2+S3＝16，则S1的值为（ ）
A．7
B．8
C．9
D．10
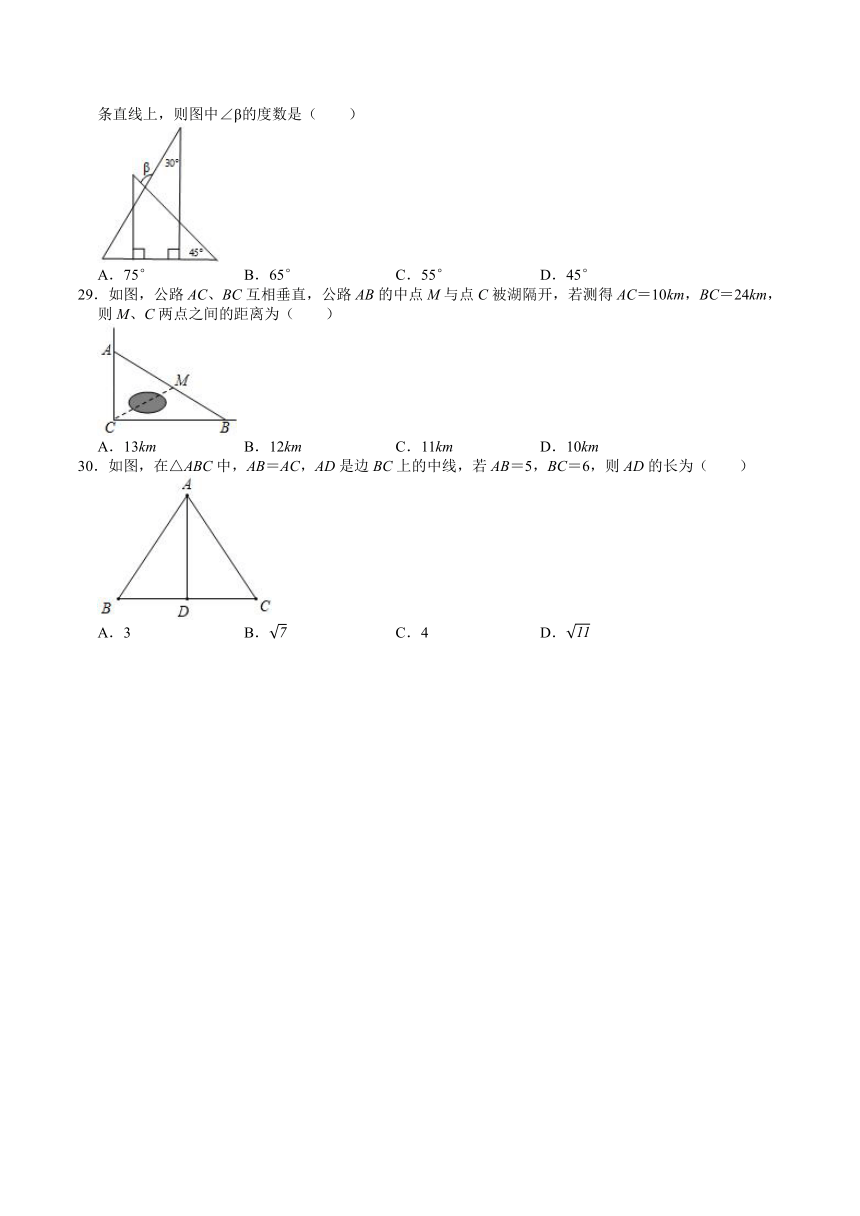
28．将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上，则图中∠β的度数是（ ）
A．75°
B．65°
C．55°
D．45°
29．如图，公路AC、BC互相垂直，公路AB的中点M与点C被湖隔开，若测得AC＝10km，BC＝24km，则M、C两点之间的距离为（ ）
A．13km
B．12km
C．11km
D．10km
30．如图，在△ABC中，AB＝AC，AD是边BC上的中线，若AB＝5，BC＝6，则AD的长为（ ）
A．3
B．
C．4
D．
2019--2020学年江苏省八年级上册数学（苏科版）期末考试《勾股定理》试题分类——选择题
参考答案与试题解析
一．选择题（共30小题）
1．【答案】B
【解答】解：设竹子折断处离地面x尺，则斜边为（9﹣x）尺，
根据勾股定理得：x2+32＝（9﹣x）2．
解得：x＝4，
答：折断处离地面的高度为4尺．
故选：B．
2．【答案】C
【解答】解：从长度分别为1，2，，的四条线段中任选取三条等可能的结果有：1，2，；1，2，；1，，；2，，；
12+（）2＝22，符合勾股定理的逆定理，能组成直角三角形；
12+22＝（）2，符合勾股定理的逆定理，能组成直角三角形；
12+（）2≠（）2，不符合勾股定理的逆定理，不能组成直角三角形；
22+（）2≠（）2，不符合勾股定理的逆定理，不能组成直角三角形．
故能组成直角三角形的个数有2个．
故选：C．
3．【答案】A
【解答】解：∵设小正方形的边长是1，连接AE、CE、BD、CE、CD、DE，
则AB＝BC＝2，BE＝4，
由勾股定理得：EC2＝AE2＝22+42＝20，DC2＝DE2＝12+32＝10，BD2＝32+32＝18，
∴AE＝EC，DC＝DE，AB2+BE2＝AE2，BC2+BE2＝CE2，CD2+DE2＝CE2，
∴等腰三角形有△AEC，△CDE，共2个；
直角三角形有△ABE，△CDE，△CBE，共3个；
故选：A．
4．【答案】C
【解答】解：由题意可得，，
∴小正方形的面积＝（a﹣b）2＝a2+b2﹣2ab＝16﹣12＝4，
故选：C．
5．【答案】A
【解答】解：由勾股定理得，斜边长为13，
故选：A．
6．【答案】B
【解答】解：连接AC，过D作DF⊥BC于F，则∠F＝90°，
在Rt△ABC中，∠ABC＝90°，AB＝3，BC＝4，由勾股定理得：AC＝5，
∵在△ACD中，AC＝5，CD＝10，AD＝5，
∴AC2+CD2＝AD2，
∴∠ACD＝90°，
∵∠ABC＝90°，
∴∠ACB+∠BAC＝90°，∠ACB+∠DCF＝90°，
∴∠BAC＝∠DCF，
∵∠ABC＝∠F＝90°，
∴△ABC∽△CFD，
∴，
∴，
设CF＝3x，DF＝4x，
在Rt△DFC中，由勾股定理得：CD2＝CF2+DF2，
即102＝（3x）2+（4x）2，
解得：x＝2（负数舍去），
即CF＝3×2＝6，DF＝4x＝8，
∴BF＝4+6＝10，
在Rt△DFB中，BD2，
故选：B．
7．【答案】C
【解答】解：∵直角三角形的两边长分别为3和4，
∴①4是此直角三角形的斜边长；
②当4是此直角三角形的直角边长时，斜边长为5．
综上所述，斜边长为4或5．
故选：C．
8．【答案】A
【解答】解：∵∠A＝90°，
∴∠B+∠C＝90°，
∵∠B﹣∠C＝30°，
∴∠B＝60°，∠C＝30°，
故选：A．
9．【答案】D
【解答】解：∵∠AOB＝∠COD＝90°，
∴∠2＝∠AOC＝25°，
∴∠1＝∠EOF﹣∠2﹣∠DOF＝90°﹣25°﹣35°＝30°，
故选：D．
10．【答案】B
【解答】解：在Rt△ABC中，AB2＝AC2+BC2，AB＝3，
S阴影＝S△AEC+S△BFC+S△ADB（）2（）2（）2
（AC2+BC2+AB2）
AB2，
32
．
故选：B．
11．【答案】D
【解答】解：A、不是勾股数，因为72+122≠132；
B、不是勾股数，因为32+42≠72；
C、不是勾股数，因为不是正整数；
D、是勾股数，因为82+152＝172；，且8，15，17是正整数．
故选：D．
12．【答案】C
【解答】解：由题可得，3＝22﹣1，4＝2×2，5＝22+1，……
∴a＝n2﹣1，b＝2n，c＝n2+1，
∴当c＝n2+1＝65时，n＝8，
∴x＝63，y＝16，
∴x+y＝79，
故选：C．
13．【答案】C
【解答】解：如右图所示，
根据勾股定理，可得
225+A＝289，
∴A＝64．
故选：C．
14．【答案】D
【解答】解：设芦苇长AB＝AB′＝x尺，则水深AC＝（x﹣1）尺，
因为边长为10尺的正方形，所以B'C＝5尺
在Rt△AB'C中，52+（x﹣1）2＝x2，
解之得x＝13，
即水深12尺，芦苇长13尺．
故选：D．
15．【答案】C
【解答】解：将此长方形折叠，使点B与点D重合，∴BE＝ED．
∵AD＝9cm＝AE+DE＝AE+BE．
∴BE＝9﹣AE，
根据勾股定理可知AB2+AE2＝BE2．
解得AE＝4．
∴△ABE的面积为3×4÷2＝6．故选C．
16．【答案】A
【解答】解：在Rt△ABC中，∠AC＝6，AB＝10，则由勾股定理知：BC8．
∴AC?BCAB?CD，则CD．
过点F作FG⊥AB于点G，
∵∠ACB＝90°，CD⊥AB，
∴∠CDA＝90°，
∴∠CAF+∠CFA＝90°，∠FAD+∠AED＝90°，
∵AF平分∠CAB，
∴∠CAF＝∠FAD，
∴∠CFA＝∠AED＝∠CEF，
∴CE＝CF，
∵AF平分∠CAB，∠ACF＝∠AGF＝90°，
∴FC＝FG，
∵∠B＝∠B，∠FGB＝∠ACB＝90°，
∴△BFG∽△BAC，
∴，
∵AC＝6，AB＝10，BC＝8，
∴，
∵FC＝FG，
∴，
解得：FC＝3，即CE的长为3．
∴DE＝CD﹣CE3．
故选：A．
17．【答案】D
【解答】解：A、22+32≠42，不能构成勾股数，故错误；
B、（）2+（）2≠（）2，不能构成勾股数，故错误；
C、62+72≠82，不能构成勾股数，故错误；
D、52+122＝132，能构成勾股数，故正确．
故选：D．
18．【答案】D
【解答】解：A、∵32+42＝52，
∴此三角形是直角三角形，不符合题意；
B、∵52+122＝132，
∴此三角形是直角三角形，不符合题意；
C、∵22+（）2＝42，
∴此三角形是直角三角形，不符合题意；
D、∵62+72≠82，
∴此三角形不是直角三角形，符合题意；
故选：D．
19．【答案】D
【解答】解：∵CE平分∠ACB，CF平分∠ACD，
∴∠ACE∠ACB，∠ACF∠ACD，即∠ECF（∠ACB+∠ACD）＝90°，
又∵EF∥BC，CE平分∠ACB，CF平分∠ACD，
∴∠ECB＝∠MEC＝∠ECM，∠DCF＝∠CFM＝∠MCF，
∴CM＝EM＝MF＝3，EF＝6，
由勾股定理可知CE2+CF2＝EF2＝36，
故选：D．
20．【答案】D
【解答】解：A、∵12+（）2＝22，
∴△ABC是直角三角形，故本选项不符合题意；
B、∵12+22＝（）2，
∴△ABC是直角三角形，故本选项不符合题意；
C、∵32+42＝52，
∴△ABC是直角三角形，故本选项不符合题意；
D、∵∠A+∠B+∠C＝180°，∠A：∠B：∠C＝3：4：5，
∴∠A＝45°，∠5＝60°，∠C＝75°，
∴△ABC不是直角三角形，故本选项符合题意；
故选：D．
21．【答案】C
【解答】解：∵∠BAC＝90°，AD⊥BC，
∴∠C+∠ABC＝90°，
∠BAD+∠ABC＝90°，
∴∠BAD＝∠C，故①正确；
∵BE是∠ABC的平分线，
∴∠ABE＝∠CBE，
∵∠ABE+∠AEF＝90°，
∠CBE+∠BFD＝90°，
∴∠AEF＝∠BFD，
又∵∠AFE＝∠BFD（对顶角相等），
∴∠AEF＝∠AFE，故②正确；
∵∠ABE＝∠CBE，
∴只有∠C＝30°时∠EBC＝∠C，故③错误；
∵∠AEF＝∠AFE，
∴AE＝AF，
∵AG平分∠DAC，
∴AG⊥EF，故④正确．
综上所述，正确的结论是①②④．
故选：C．
22．【答案】D
【解答】解：A、∠C﹣∠B＝∠A，即∠A+∠B＝∠C，又∵∠A+∠B+∠C＝180°，则∠C＝90°，那么△ABC是直角三角形，说法正确；
B、c2＝b2﹣a2，即a2+c2＝b2，那么△ABC是直角三角形且∠B＝90，说法正确；
C、∠A：∠B：∠C＝1：2：3，又∵∠A+∠B+∠C＝180°，则∠C＝90°，则△ABC是直角三角形，说法正确；
D、a＝3，b＝5，c＝4，32+52≠42，但是32+42＝52，则△ABC可能是直角三角形，故原来说法错误．
故选：D．
23．【答案】D
【解答】解：∵AD是∠CAB的平分线，∠C＝90°，DE⊥AB，
∴CD＝DE，
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴AE＝AC＝5cm，
由勾股定理得，AB13cm，
∴BE＝AB﹣AE＝13﹣5＝8cm，
∴△BDE的周长＝BE+BD+CD＝BE+BD+CD＝BE+BC＝8+12＝20cm．
故选：D．
24．【答案】C
【解答】解：依题意得：x2﹣4＝0，y2﹣3＝0，
∴x＝2，y，
斜边长，
所以正方形的面积＝（）2＝7．
故选：C．
25．【答案】C
【解答】解：A、∠A+∠B＝∠C，又∠A+∠B+∠C＝180°，则∠C＝90°，是直角三角形；
B、∠A：∠B：∠C＝1：2：3，又∠A+∠B+∠C＝180°，则∠C＝90°，是直角三角形；
C、（x）2+（2x）2≠（3x）2，不符合勾股定理的逆定理，不是直角三角形；
D、由a2﹣b2＝c2，得c2+b2＝a2，符合勾股定理的逆定理，是直角三角形．
故选：C．
26．【答案】D
【解答】解：如图，作BD⊥OC于点D，
由题意得：AO＝BD＝3m，AB＝OD＝2m，
∵OC＝6m，
∴DC＝4m，
∴由勾股定理得：BC5（m），
∴大树的高度为5+5＝10（m），
故选：D．
27．【答案】B
【解答】解：∵由勾股定理得：AC2+BC2＝AB2，
∴S3+S2＝S1，
∵S1+S2+S3＝16，
∴2S1＝16，
∴S1＝8，
故选：B．
28．【答案】A
【解答】解：如图所示：
∵△ACG和△BDE是直角三角形，∠AGC＝90°，∠B＝45°，∠C＝30°，
∴∠CFD＝∠BFG＝90°﹣45°＝45°，
∴∠β＝∠C+∠CFD＝30°+45°＝75°；
故选：A．
29．【答案】A
【解答】解：在Rt△ABC中，AB2＝AC2+CB2
∵AC＝10km，BC＝24km，
∴AB＝26km，
∵M点是AB中点
∴MCAB＝13km，
故选：A．
30．【答案】C
【解答】解：∵在△ABC中，AB＝AC，AD是边BC上的中线，
∴BDBC＝3，AD⊥BC，
∵在Rt△ADB中，AB＝5，
∴AD4．
故选：C．
1．古代数学的“折竹抵地”问题：“今有竹高九尺，末折抵地，去本三尺，问折者高几何？”意思是：现有竹子高9尺，折后竹尖抵地与竹子底部的距离为3尺，问折处高几尺？即：如图，AB+AC＝9尺，BC＝3尺，则AC等于（ ）尺．
A．3.5
B．4
C．4.5
D．5
2．在四条长度分别是1，2，，的线段中，以其中的三条线段长作为边，能组成直角三角形的个数有（ ）
A．0个
B．1个
C．2个
D．3个
3．如图，方格中的点A、B、C、D、E称为“格点”（格线的交点），以这5个格点中的3点为顶点画三角形，可以画等腰三角形和直角三角形的个数分别是（ ）
A．2和3
B．3和3
C．2和4
D．3和4
4．“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b．若ab＝6，大正方形的面积为16，则小正方形的面积为（ ）
A．8
B．6
C．4
D．3
5．已知直角三角形两直角边长分别为5，12，则斜边长为（ ）
A．13
B．14
C．15
D．16
6．如图，在四边形ABCD中，∠ABC＝90°，AB＝3，BC＝4，CD＝10，AD＝5，则BD等于（ ）
A．13
B．2
C．8
D．6
7．已知直角三角形的两边长分别为3和4，则斜边长为（ ）
A．4
B．5
C．4或5
D．5或
8．若△ABC中，∠A＝90°，且∠B﹣∠C＝30°，那么∠C的度数为（ ）
A．30°
B．40°
C．50°
D．60°
9．如图，若将三个含45°的直角三角板的直角顶点重合放置，则∠1的度数为（ ）
A．15°
B．20°
C．25°
D．30°
10．如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB＝3，则图中的阴影部分的面积（ ）
A．9
B．
C．
D．3
11．下列各组数为勾股数的是（ ）
A．7，12，13
B．3，4，7
C．3，4，6
D．8，15，17
12．如果正整数a、b、c满足等式a2+b2＝c2，那么正整数a、b、c叫做勾股数，某同学将自己探究勾股数的过程列成下表，观察表中每列数的规律，可知x+y的值为（ ）
A．47
B．62
C．79
D．98
13．如图所示：已知两个正方形的面积，则字母A所代表的正方形的面积为（ ）
A．4
B．8
C．64
D．16
14．如图，有一个池塘，其底面是边长为10尺的正方形，一个芦苇AB生长在它的中央，高出水面部分BC为1尺．如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′．则这根芦苇的长度是（ ）
A．10尺
B．11尺
C．12尺
D．13尺
15．已知，如图长方形ABCD中，AB＝3cm，AD＝9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（ ）
A．3cm2
B．4cm2
C．6cm2
D．12cm2
16．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD于点E，交CB于点F．若AC＝6，AB＝10，则DE的长为（ ）
A．
B．3
C．
D．
17．下列为勾股数的是（ ）
A．2，3，4
B．，，
C．6，7，8
D．5，12，13
18．下列长度的三条线段不能构成直角三角形的是（ ）
A．3、4、5
B．5、12、13
C．2、4、
D．6、7、8
19．如图，在△ABC中，CE平分∠ACB，CF平分∠ACD，且EF∥BC交AC于M，若CM＝3，则CE2+CF2的值为（ ）
A．6
B．9
C．18
D．36
20．满足下列条件的△ABC不是直角三角形的是（ ）
A．BC＝1，AC＝2，AB
B．BC＝1，AC＝2，AB
C．BC：AC：AB＝3：4：5
D．∠A：∠B：∠C＝3：4：5
21．如图，△ABC中，∠BAC＝90°，AD⊥BC，∠ABC的平分线BE交AD于点F，AG平分∠DAC．给出下列结论：①∠BAD＝∠C；
②∠AEF＝∠AFE；
③∠EBC＝∠C；④AG⊥EF．正确结论有（ ）
A．1个
B．2个
C．3个
D．4个
22．在△ABC中，∠A、∠B、∠C的对边分别是a、b、c，下列说法错误的是（ ）
A．如果∠C﹣∠B＝∠A，则△ABC是直角三角形
B．如果c2＝b2﹣a2，则△ABC是直角三角形
C．如果∠A：∠B：∠C＝1：2：3，则△ABC是直角三角形
D．如果a2+b2≠c2，则△ABC不是直角三角形
23．如图，在
Rt△ABC中，∠C＝90°，AC＝5
cm，BC＝12
cm，∠CAB的平分线交BC于D，过点D作DE⊥AB于E，则△BDE的周长为（ ）
A．17
B．18
C．19
D．20
24．已知x、y为正数，且|x2﹣4|+（y2﹣3）2＝0，如果以x、y的长为直角边作一个直角三角形，那么以这个直角三角形的斜边为边长的正方形的面积为（ ）
A．5
B．25
C．7
D．15
25．由下列条件不能判定△ABC为直角三角形的是（ ）
A．∠A+∠B＝∠C
B．∠A：∠B：∠C＝1：2：3
C．a：b：c＝1：2：3
D．a2﹣b2＝c2
26．如图，一棵大树在离地面3m，5m两处折成三段，中间一段AB恰好与地面平行，大树顶部落在离大树底部6m处，则大树折断前的高度是（ ）
A．9m
B．14m
C．11m
D．10m
27．如图，以Rt△ABC的三边为边，分别向外作正方形，它们的面积分别为S1、S2、S3，若S1+S2+S3＝16，则S1的值为（ ）
A．7
B．8
C．9
D．10
28．将一副直角三角板如图放置，使含30°角的三角板的直角边和含45°角的三角板的一条直角边在同一条直线上，则图中∠β的度数是（ ）
A．75°
B．65°
C．55°
D．45°
29．如图，公路AC、BC互相垂直，公路AB的中点M与点C被湖隔开，若测得AC＝10km，BC＝24km，则M、C两点之间的距离为（ ）
A．13km
B．12km
C．11km
D．10km
30．如图，在△ABC中，AB＝AC，AD是边BC上的中线，若AB＝5，BC＝6，则AD的长为（ ）
A．3
B．
C．4
D．
2019--2020学年江苏省八年级上册数学（苏科版）期末考试《勾股定理》试题分类——选择题
参考答案与试题解析
一．选择题（共30小题）
1．【答案】B
【解答】解：设竹子折断处离地面x尺，则斜边为（9﹣x）尺，
根据勾股定理得：x2+32＝（9﹣x）2．
解得：x＝4，
答：折断处离地面的高度为4尺．
故选：B．
2．【答案】C
【解答】解：从长度分别为1，2，，的四条线段中任选取三条等可能的结果有：1，2，；1，2，；1，，；2，，；
12+（）2＝22，符合勾股定理的逆定理，能组成直角三角形；
12+22＝（）2，符合勾股定理的逆定理，能组成直角三角形；
12+（）2≠（）2，不符合勾股定理的逆定理，不能组成直角三角形；
22+（）2≠（）2，不符合勾股定理的逆定理，不能组成直角三角形．
故能组成直角三角形的个数有2个．
故选：C．
3．【答案】A
【解答】解：∵设小正方形的边长是1，连接AE、CE、BD、CE、CD、DE，
则AB＝BC＝2，BE＝4，
由勾股定理得：EC2＝AE2＝22+42＝20，DC2＝DE2＝12+32＝10，BD2＝32+32＝18，
∴AE＝EC，DC＝DE，AB2+BE2＝AE2，BC2+BE2＝CE2，CD2+DE2＝CE2，
∴等腰三角形有△AEC，△CDE，共2个；
直角三角形有△ABE，△CDE，△CBE，共3个；
故选：A．
4．【答案】C
【解答】解：由题意可得，，
∴小正方形的面积＝（a﹣b）2＝a2+b2﹣2ab＝16﹣12＝4，
故选：C．
5．【答案】A
【解答】解：由勾股定理得，斜边长为13，
故选：A．
6．【答案】B
【解答】解：连接AC，过D作DF⊥BC于F，则∠F＝90°，
在Rt△ABC中，∠ABC＝90°，AB＝3，BC＝4，由勾股定理得：AC＝5，
∵在△ACD中，AC＝5，CD＝10，AD＝5，
∴AC2+CD2＝AD2，
∴∠ACD＝90°，
∵∠ABC＝90°，
∴∠ACB+∠BAC＝90°，∠ACB+∠DCF＝90°，
∴∠BAC＝∠DCF，
∵∠ABC＝∠F＝90°，
∴△ABC∽△CFD，
∴，
∴，
设CF＝3x，DF＝4x，
在Rt△DFC中，由勾股定理得：CD2＝CF2+DF2，
即102＝（3x）2+（4x）2，
解得：x＝2（负数舍去），
即CF＝3×2＝6，DF＝4x＝8，
∴BF＝4+6＝10，
在Rt△DFB中，BD2，
故选：B．
7．【答案】C
【解答】解：∵直角三角形的两边长分别为3和4，
∴①4是此直角三角形的斜边长；
②当4是此直角三角形的直角边长时，斜边长为5．
综上所述，斜边长为4或5．
故选：C．
8．【答案】A
【解答】解：∵∠A＝90°，
∴∠B+∠C＝90°，
∵∠B﹣∠C＝30°，
∴∠B＝60°，∠C＝30°，
故选：A．
9．【答案】D
【解答】解：∵∠AOB＝∠COD＝90°，
∴∠2＝∠AOC＝25°，
∴∠1＝∠EOF﹣∠2﹣∠DOF＝90°﹣25°﹣35°＝30°，
故选：D．
10．【答案】B
【解答】解：在Rt△ABC中，AB2＝AC2+BC2，AB＝3，
S阴影＝S△AEC+S△BFC+S△ADB（）2（）2（）2
（AC2+BC2+AB2）
AB2，
32
．
故选：B．
11．【答案】D
【解答】解：A、不是勾股数，因为72+122≠132；
B、不是勾股数，因为32+42≠72；
C、不是勾股数，因为不是正整数；
D、是勾股数，因为82+152＝172；，且8，15，17是正整数．
故选：D．
12．【答案】C
【解答】解：由题可得，3＝22﹣1，4＝2×2，5＝22+1，……
∴a＝n2﹣1，b＝2n，c＝n2+1，
∴当c＝n2+1＝65时，n＝8，
∴x＝63，y＝16，
∴x+y＝79，
故选：C．
13．【答案】C
【解答】解：如右图所示，
根据勾股定理，可得
225+A＝289，
∴A＝64．
故选：C．
14．【答案】D
【解答】解：设芦苇长AB＝AB′＝x尺，则水深AC＝（x﹣1）尺，
因为边长为10尺的正方形，所以B'C＝5尺
在Rt△AB'C中，52+（x﹣1）2＝x2，
解之得x＝13，
即水深12尺，芦苇长13尺．
故选：D．
15．【答案】C
【解答】解：将此长方形折叠，使点B与点D重合，∴BE＝ED．
∵AD＝9cm＝AE+DE＝AE+BE．
∴BE＝9﹣AE，
根据勾股定理可知AB2+AE2＝BE2．
解得AE＝4．
∴△ABE的面积为3×4÷2＝6．故选C．
16．【答案】A
【解答】解：在Rt△ABC中，∠AC＝6，AB＝10，则由勾股定理知：BC8．
∴AC?BCAB?CD，则CD．
过点F作FG⊥AB于点G，
∵∠ACB＝90°，CD⊥AB，
∴∠CDA＝90°，
∴∠CAF+∠CFA＝90°，∠FAD+∠AED＝90°，
∵AF平分∠CAB，
∴∠CAF＝∠FAD，
∴∠CFA＝∠AED＝∠CEF，
∴CE＝CF，
∵AF平分∠CAB，∠ACF＝∠AGF＝90°，
∴FC＝FG，
∵∠B＝∠B，∠FGB＝∠ACB＝90°，
∴△BFG∽△BAC，
∴，
∵AC＝6，AB＝10，BC＝8，
∴，
∵FC＝FG，
∴，
解得：FC＝3，即CE的长为3．
∴DE＝CD﹣CE3．
故选：A．
17．【答案】D
【解答】解：A、22+32≠42，不能构成勾股数，故错误；
B、（）2+（）2≠（）2，不能构成勾股数，故错误；
C、62+72≠82，不能构成勾股数，故错误；
D、52+122＝132，能构成勾股数，故正确．
故选：D．
18．【答案】D
【解答】解：A、∵32+42＝52，
∴此三角形是直角三角形，不符合题意；
B、∵52+122＝132，
∴此三角形是直角三角形，不符合题意；
C、∵22+（）2＝42，
∴此三角形是直角三角形，不符合题意；
D、∵62+72≠82，
∴此三角形不是直角三角形，符合题意；
故选：D．
19．【答案】D
【解答】解：∵CE平分∠ACB，CF平分∠ACD，
∴∠ACE∠ACB，∠ACF∠ACD，即∠ECF（∠ACB+∠ACD）＝90°，
又∵EF∥BC，CE平分∠ACB，CF平分∠ACD，
∴∠ECB＝∠MEC＝∠ECM，∠DCF＝∠CFM＝∠MCF，
∴CM＝EM＝MF＝3，EF＝6，
由勾股定理可知CE2+CF2＝EF2＝36，
故选：D．
20．【答案】D
【解答】解：A、∵12+（）2＝22，
∴△ABC是直角三角形，故本选项不符合题意；
B、∵12+22＝（）2，
∴△ABC是直角三角形，故本选项不符合题意；
C、∵32+42＝52，
∴△ABC是直角三角形，故本选项不符合题意；
D、∵∠A+∠B+∠C＝180°，∠A：∠B：∠C＝3：4：5，
∴∠A＝45°，∠5＝60°，∠C＝75°，
∴△ABC不是直角三角形，故本选项符合题意；
故选：D．
21．【答案】C
【解答】解：∵∠BAC＝90°，AD⊥BC，
∴∠C+∠ABC＝90°，
∠BAD+∠ABC＝90°，
∴∠BAD＝∠C，故①正确；
∵BE是∠ABC的平分线，
∴∠ABE＝∠CBE，
∵∠ABE+∠AEF＝90°，
∠CBE+∠BFD＝90°，
∴∠AEF＝∠BFD，
又∵∠AFE＝∠BFD（对顶角相等），
∴∠AEF＝∠AFE，故②正确；
∵∠ABE＝∠CBE，
∴只有∠C＝30°时∠EBC＝∠C，故③错误；
∵∠AEF＝∠AFE，
∴AE＝AF，
∵AG平分∠DAC，
∴AG⊥EF，故④正确．
综上所述，正确的结论是①②④．
故选：C．
22．【答案】D
【解答】解：A、∠C﹣∠B＝∠A，即∠A+∠B＝∠C，又∵∠A+∠B+∠C＝180°，则∠C＝90°，那么△ABC是直角三角形，说法正确；
B、c2＝b2﹣a2，即a2+c2＝b2，那么△ABC是直角三角形且∠B＝90，说法正确；
C、∠A：∠B：∠C＝1：2：3，又∵∠A+∠B+∠C＝180°，则∠C＝90°，则△ABC是直角三角形，说法正确；
D、a＝3，b＝5，c＝4，32+52≠42，但是32+42＝52，则△ABC可能是直角三角形，故原来说法错误．
故选：D．
23．【答案】D
【解答】解：∵AD是∠CAB的平分线，∠C＝90°，DE⊥AB，
∴CD＝DE，
在Rt△ACD和Rt△AED中，
，
∴Rt△ACD≌Rt△AED（HL），
∴AE＝AC＝5cm，
由勾股定理得，AB13cm，
∴BE＝AB﹣AE＝13﹣5＝8cm，
∴△BDE的周长＝BE+BD+CD＝BE+BD+CD＝BE+BC＝8+12＝20cm．
故选：D．
24．【答案】C
【解答】解：依题意得：x2﹣4＝0，y2﹣3＝0，
∴x＝2，y，
斜边长，
所以正方形的面积＝（）2＝7．
故选：C．
25．【答案】C
【解答】解：A、∠A+∠B＝∠C，又∠A+∠B+∠C＝180°，则∠C＝90°，是直角三角形；
B、∠A：∠B：∠C＝1：2：3，又∠A+∠B+∠C＝180°，则∠C＝90°，是直角三角形；
C、（x）2+（2x）2≠（3x）2，不符合勾股定理的逆定理，不是直角三角形；
D、由a2﹣b2＝c2，得c2+b2＝a2，符合勾股定理的逆定理，是直角三角形．
故选：C．
26．【答案】D
【解答】解：如图，作BD⊥OC于点D，
由题意得：AO＝BD＝3m，AB＝OD＝2m，
∵OC＝6m，
∴DC＝4m，
∴由勾股定理得：BC5（m），
∴大树的高度为5+5＝10（m），
故选：D．
27．【答案】B
【解答】解：∵由勾股定理得：AC2+BC2＝AB2，
∴S3+S2＝S1，
∵S1+S2+S3＝16，
∴2S1＝16，
∴S1＝8，
故选：B．
28．【答案】A
【解答】解：如图所示：
∵△ACG和△BDE是直角三角形，∠AGC＝90°，∠B＝45°，∠C＝30°，
∴∠CFD＝∠BFG＝90°﹣45°＝45°，
∴∠β＝∠C+∠CFD＝30°+45°＝75°；
故选：A．
29．【答案】A
【解答】解：在Rt△ABC中，AB2＝AC2+CB2
∵AC＝10km，BC＝24km，
∴AB＝26km，
∵M点是AB中点
∴MCAB＝13km，
故选：A．
30．【答案】C
【解答】解：∵在△ABC中，AB＝AC，AD是边BC上的中线，
∴BDBC＝3，AD⊥BC，
∵在Rt△ADB中，AB＝5，
∴AD4．
故选：C．
同课章节目录