沪教版数学六年级上册《扇形的面积》ppt课件
文档属性
| 名称 | 沪教版数学六年级上册《扇形的面积》ppt课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 275.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-10 00:00:00 | ||
图片预览



文档简介
(共12张PPT)
扇形的面积
沪教版六年级数学上册
教学目标
1. 理解扇形的概念以及圆心角和扇形面积的关系,理解扇形面积公式的推导过程,能用公式进行有关的面积计算。
2. 提高概括、归纳以及知识的迁移能力。
3. 培养从实际生活中发现问题、解决问题、运用所学知识进行综合分析的能力。
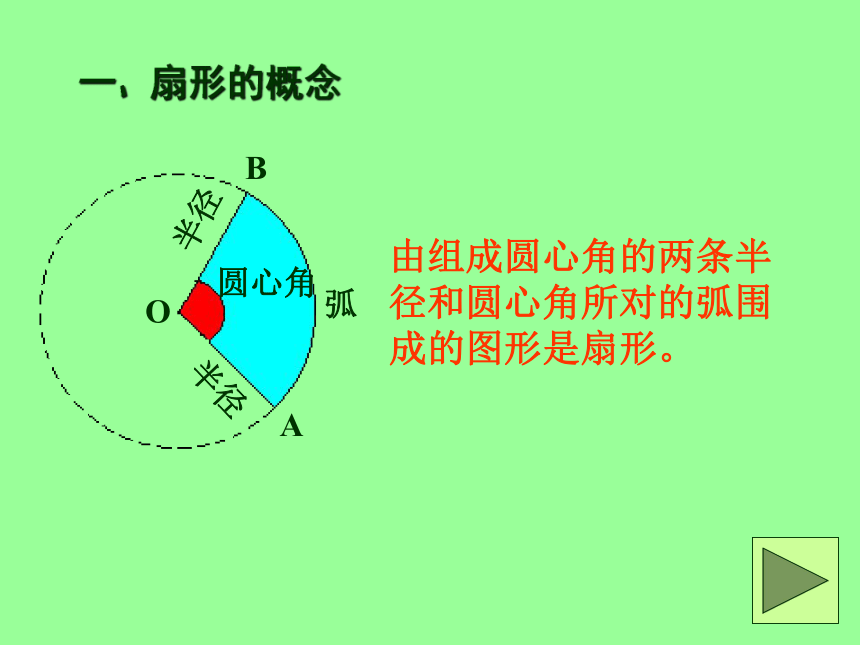
一、扇形的概念
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
圆心角
弧
B
A
O
圆心角
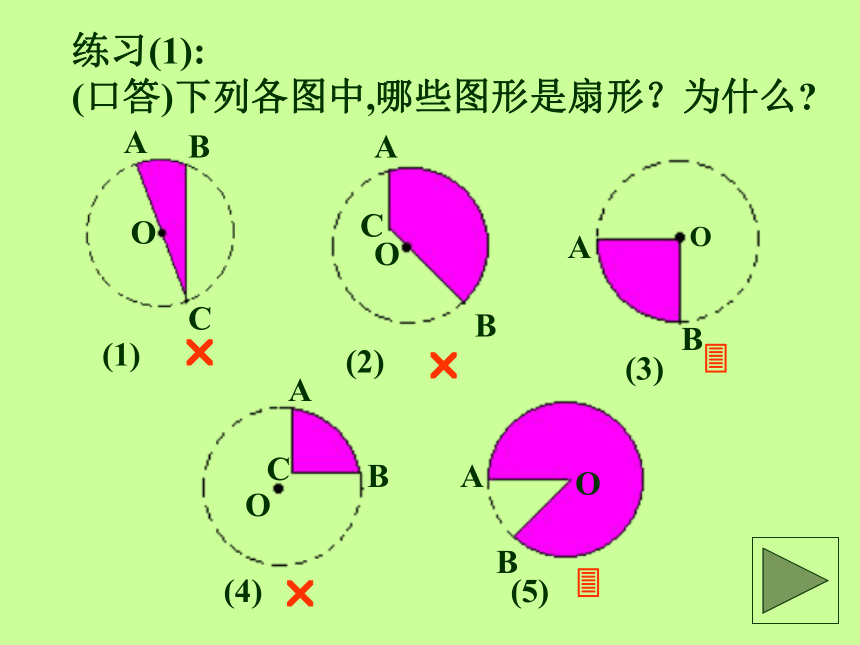
练习(1):
(口答)下列各图中,哪些图形是扇形?为什么
A
B
O
C
O
A
B
C
O
A
O
C
A
B
O
A
B
(1)
(2)
(3)
(4)
(5)
B
二、扇形的面积
1.思考1:
圆心角的大小与扇形的面积有什么关系
思考2:如果要知道圆心角分别为60 、120 、
270 的扇形面积是多少?先要知道
什么?
得出:
扇形的面积随着圆心角的增大而增大
思考3: 圆心角是1 的扇形面积是圆面积的几
分之几
圆心角是n 的扇形面积是圆面积的几
分之几
1
得出:
圆心角为1°的扇形面积是
圆面积的
圆心角为n 的扇形面积是圆面积的
2.练习(2):下面圆中的扇形面积各是圆面积的几分之几?
并说明理由。
180
270
36
120
60
90
r
4. 根椐以上公式
圆心角是60 的扇形面积
圆心角是120 的扇形面积
3.如果用字母表示:S表示扇形的面积,n表示圆
心角的度数,r表示圆半径
S =
那么扇形面积公式
圆心角是270 的扇形面积
5.练习:
根据下列扇形的半径r和圆心角n,求扇
形的面积
(1) r=12cm; n=120 ;
(2) r=10cm; n=225 ;
三、1. 例题: 求图中红色部分的面积
72
10
n=360-72=288
2.练习: 量一量、算一算:
140
1.8
4.396
3.96
解:r=10cm
≈ 251(cm2)
今天学习了哪些知识?有何收获?
(1)扇形的定义。
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
(2)扇形的面积公式以及推导过程。
四、总结
r
S =
扇形面积公式
扇形的面积
沪教版六年级数学上册
教学目标
1. 理解扇形的概念以及圆心角和扇形面积的关系,理解扇形面积公式的推导过程,能用公式进行有关的面积计算。
2. 提高概括、归纳以及知识的迁移能力。
3. 培养从实际生活中发现问题、解决问题、运用所学知识进行综合分析的能力。
一、扇形的概念
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
半径
半径
圆心角
弧
B
A
O
圆心角
练习(1):
(口答)下列各图中,哪些图形是扇形?为什么
A
B
O
C
O
A
B
C
O
A
O
C
A
B
O
A
B
(1)
(2)
(3)
(4)
(5)
B
二、扇形的面积
1.思考1:
圆心角的大小与扇形的面积有什么关系
思考2:如果要知道圆心角分别为60 、120 、
270 的扇形面积是多少?先要知道
什么?
得出:
扇形的面积随着圆心角的增大而增大
思考3: 圆心角是1 的扇形面积是圆面积的几
分之几
圆心角是n 的扇形面积是圆面积的几
分之几
1
得出:
圆心角为1°的扇形面积是
圆面积的
圆心角为n 的扇形面积是圆面积的
2.练习(2):下面圆中的扇形面积各是圆面积的几分之几?
并说明理由。
180
270
36
120
60
90
r
4. 根椐以上公式
圆心角是60 的扇形面积
圆心角是120 的扇形面积
3.如果用字母表示:S表示扇形的面积,n表示圆
心角的度数,r表示圆半径
S =
那么扇形面积公式
圆心角是270 的扇形面积
5.练习:
根据下列扇形的半径r和圆心角n,求扇
形的面积
(1) r=12cm; n=120 ;
(2) r=10cm; n=225 ;
三、1. 例题: 求图中红色部分的面积
72
10
n=360-72=288
2.练习: 量一量、算一算:
140
1.8
4.396
3.96
解:r=10cm
≈ 251(cm2)
今天学习了哪些知识?有何收获?
(1)扇形的定义。
由组成圆心角的两条半径和圆心角所对的弧围成的图形是扇形。
(2)扇形的面积公式以及推导过程。
四、总结
r
S =
扇形面积公式
