5.2 活用判定两直线平行的六种方法(共13张ppt)
文档属性
| 名称 | 5.2 活用判定两直线平行的六种方法(共13张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 17:15:58 | ||
图片预览



文档简介
(共13张PPT)
5.2
平行线及其判定
第4课时
活用判定两直线平行的六种方法
第五章
相交线与平行线
1.下面几种说法中,正确的是( )
A.同一平面内不相交的两条线段平行
B.同一平面内不相交的两条射线平行
C.同一平面内不相交的两条直线平行
D.以上三种说法都不正确
1
方法
利用平行线的定义
C
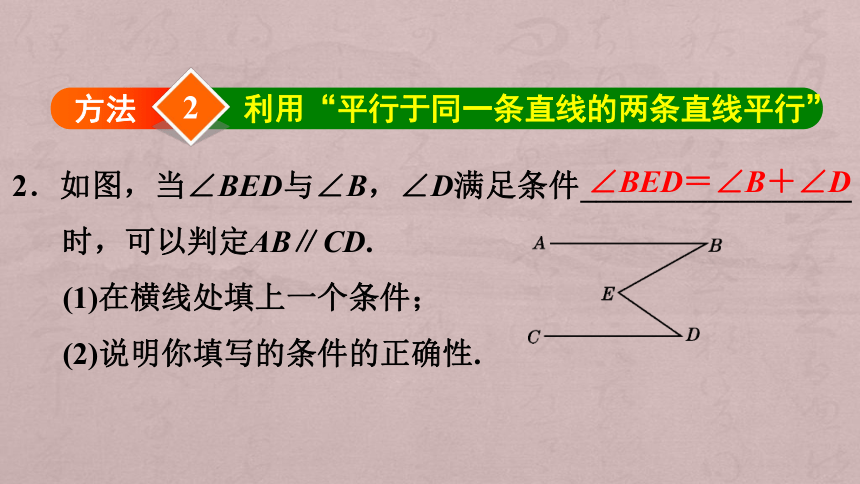
2.如图,当∠BED与∠B,∠D满足条件_________________时,可以判定AB∥CD.
(1)在横线处填上一个条件;
(2)说明你填写的条件的正确性.
2
方法
利用“平行于同一条直线的两条直线平行”
∠BED=∠B+∠D
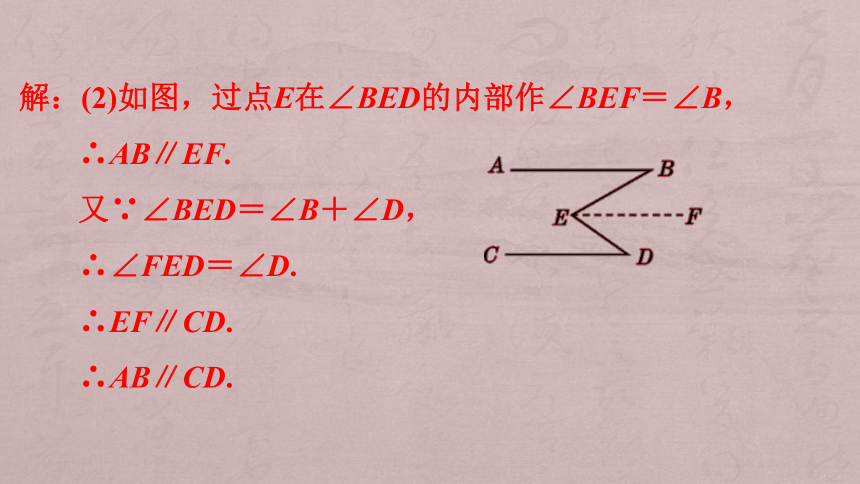
解:(2)如图,过点E在∠BED的内部作∠BEF=∠B,
∴AB∥EF.
又∵∠BED=∠B+∠D,
∴∠FED=∠D.
∴EF∥CD.
∴AB∥CD.
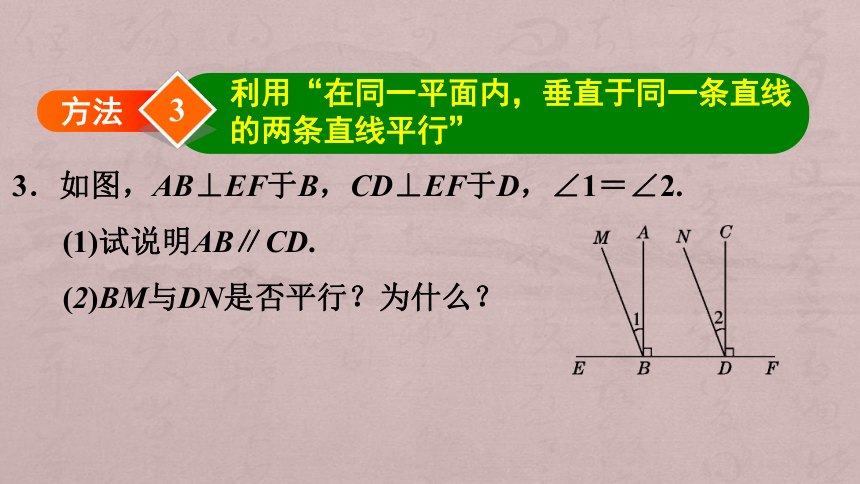
3.如图,AB⊥EF于B,CD⊥EF于D,∠1=∠2.
(1)试说明AB∥CD.
(2)BM与DN是否平行?为什么?
3
方法
利用“在同一平面内,垂直于同一条直线的两条直线平行”
解:(1)∵AB⊥EF,CD⊥EF,
∴AB∥CD.
(2)BM∥DN.理由如下:
∵AB⊥EF,CD⊥EF,
∴∠ABE=∠CDE=90°.
又∵∠1=∠2,
∴∠ABE-∠1=∠CDE-∠2,
即∠MBE=∠NDE.
∴BM∥DN.
4.如图,已知∠ABC=∠ACB,∠1=∠2,∠3=∠F.
试判断EC与DF是否平行,并说明理由.
4
方法
利用“同位角相等,两直线平行”
解:EC∥DF.理由如下:
∵∠ABC=∠ACB,∠1=∠2,
∴∠3=∠ECB.
又∵∠3=∠F,
∴∠ECB=∠F.
∴EC∥DF.
5.如图,已知∠AED=60°,∠BDE=30°,EF平分∠AED,可以判定EF∥BD吗?为什么?
5
方法
利用“内错角相等,两直线平行”
解:可以判定EF∥BD.理由如下:
∵∠AED=60°,EF平分∠AED,
∴∠FED=30°.
又∵∠BDE=30°,
∴∠FED=∠BDE.
∴EF∥BD.
6.如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°.试判断AB与CD的位置关系,并说明理由.
6
方法
利用“同旁内角互补,两直线平行”
解:AB∥CD.理由如下:
∵BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,
∴∠ABD+∠CDB=2∠1+2∠2=2(∠1+∠2)=180°.
∴AB∥CD.
5.2
平行线及其判定
第4课时
活用判定两直线平行的六种方法
第五章
相交线与平行线
1.下面几种说法中,正确的是( )
A.同一平面内不相交的两条线段平行
B.同一平面内不相交的两条射线平行
C.同一平面内不相交的两条直线平行
D.以上三种说法都不正确
1
方法
利用平行线的定义
C
2.如图,当∠BED与∠B,∠D满足条件_________________时,可以判定AB∥CD.
(1)在横线处填上一个条件;
(2)说明你填写的条件的正确性.
2
方法
利用“平行于同一条直线的两条直线平行”
∠BED=∠B+∠D
解:(2)如图,过点E在∠BED的内部作∠BEF=∠B,
∴AB∥EF.
又∵∠BED=∠B+∠D,
∴∠FED=∠D.
∴EF∥CD.
∴AB∥CD.
3.如图,AB⊥EF于B,CD⊥EF于D,∠1=∠2.
(1)试说明AB∥CD.
(2)BM与DN是否平行?为什么?
3
方法
利用“在同一平面内,垂直于同一条直线的两条直线平行”
解:(1)∵AB⊥EF,CD⊥EF,
∴AB∥CD.
(2)BM∥DN.理由如下:
∵AB⊥EF,CD⊥EF,
∴∠ABE=∠CDE=90°.
又∵∠1=∠2,
∴∠ABE-∠1=∠CDE-∠2,
即∠MBE=∠NDE.
∴BM∥DN.
4.如图,已知∠ABC=∠ACB,∠1=∠2,∠3=∠F.
试判断EC与DF是否平行,并说明理由.
4
方法
利用“同位角相等,两直线平行”
解:EC∥DF.理由如下:
∵∠ABC=∠ACB,∠1=∠2,
∴∠3=∠ECB.
又∵∠3=∠F,
∴∠ECB=∠F.
∴EC∥DF.
5.如图,已知∠AED=60°,∠BDE=30°,EF平分∠AED,可以判定EF∥BD吗?为什么?
5
方法
利用“内错角相等,两直线平行”
解:可以判定EF∥BD.理由如下:
∵∠AED=60°,EF平分∠AED,
∴∠FED=30°.
又∵∠BDE=30°,
∴∠FED=∠BDE.
∴EF∥BD.
6.如图,BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°.试判断AB与CD的位置关系,并说明理由.
6
方法
利用“同旁内角互补,两直线平行”
解:AB∥CD.理由如下:
∵BE平分∠ABD,DE平分∠BDC,∠1+∠2=90°,
∴∠ABD+∠CDB=2∠1+2∠2=2(∠1+∠2)=180°.
∴AB∥CD.
