5.3 相交线、平行线中角的计算的四种常见题型(共15张ppt)
文档属性
| 名称 | 5.3 相交线、平行线中角的计算的四种常见题型(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 17:17:32 | ||
图片预览




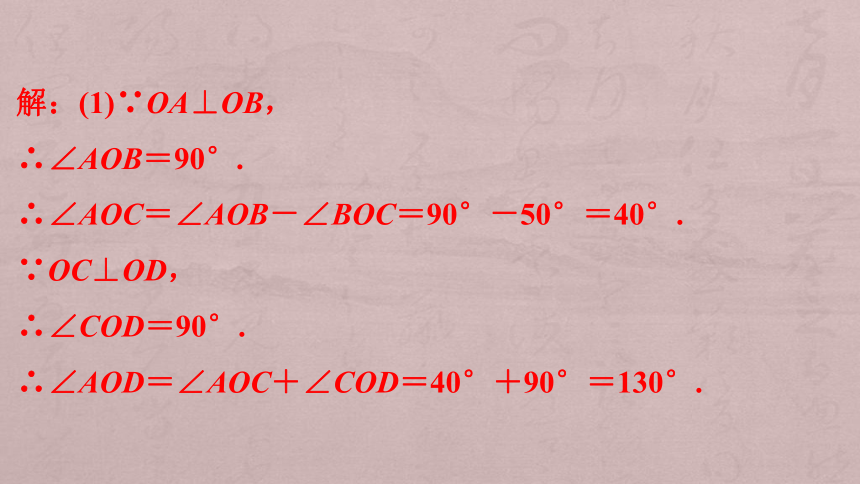
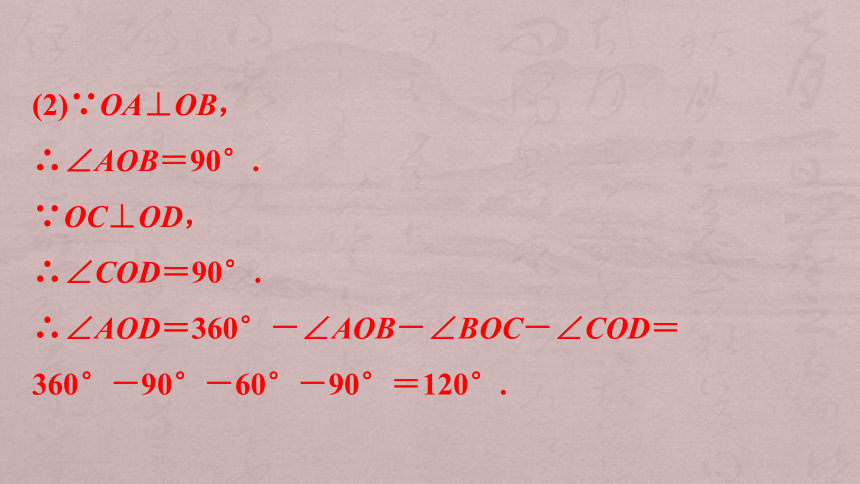
文档简介
(共15张PPT)
5.3
平行线的性质
第4课时
相交线、平行线中角的计算的四种常见题型
第五章
相交线与平行线
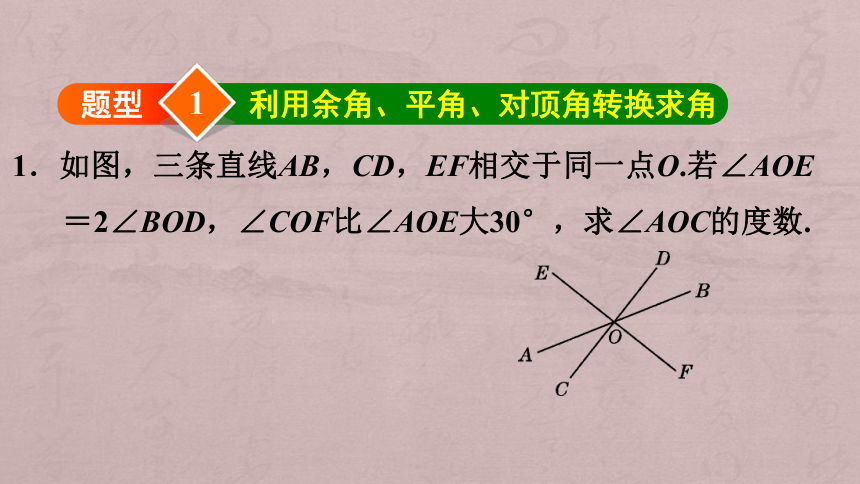
1.如图,三条直线AB,CD,EF相交于同一点O.若∠AOE=2∠BOD,∠COF比∠AOE大30°,求∠AOC的度数.
1
题型
利用余角、平角、对顶角转换求角
解:设∠AOC=x°,则∠BOD=∠AOC=x°.
∴∠AOE=2∠BOD=2x°,
∠COF=∠AOE+30°=2x°+30°.
∵∠AOE+∠AOC+∠COF=180°,
∴2x+x+2x+30=180,解得x=30.
∴∠AOC=30°.
2.已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD的度数;
(2)如图②,若∠BOC=60°,求∠AOD的度数;
2
题型
利用垂线求角
(3)根据(1)(2)的结果猜想∠AOD与∠BOC有怎样的关系,并根据图①说明理由;
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠BOC和∠AOD的度数.
解:(1)∵OA⊥OB,
∴∠AOB=90°.
∴∠AOC=∠AOB-∠BOC=90°-50°=40°.
∵OC⊥OD,
∴∠COD=90°.
∴∠AOD=∠AOC+∠COD=40°+90°=130°.
(2)∵OA⊥OB,
∴∠AOB=90°.
∵OC⊥OD,
∴∠COD=90°.
∴∠AOD=360°-∠AOB-∠BOC-∠COD=
360°-90°-60°-90°=120°.
(3)∠AOD与∠BOC互补.理由如下:
∵OA⊥OB,∴∠AOB=90°.
∴∠AOC=∠AOB-∠BOC=90°-∠BOC.
∵OC⊥OD,∴∠COD=90°.
∴∠AOD=∠AOC+∠COD=90°-∠BOC+90°=180°-∠BOC.
∴∠AOD+∠BOC=180°,即∠AOD与∠BOC互补.
(4)由(3)可知∠BOC+∠AOD=180°,
∴∠BOC=
×180°=35°,
∠AOD=180°-∠BOC=145°.
3.(中考·重庆)如图,AB∥CD,三角形EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD.若∠EFG=90°,∠E=35°,求∠EFB的度数.
3
题型
直接利用平行线的性质求角
解:∵在三角形EFG中,∠EFG=90°,∠E=35°,
∴∠EGF=180°-90°-35°=55°.
∵GE平分∠FGD,
∴∠EGF=∠EGD=55°.
∵AB∥CD,
∴∠EHB=∠EGD=55°.
又∵∠EHB=180°-∠AHE=∠EFB+∠E,
∴∠EFB=∠EHB-∠E=55°-35°=20°.
4.(中考·宿迁)如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )
A.80°
B.85°
C.95°
D.100°
4
题型
综合应用平行线的性质与判定求角
B
5.如图,∠1+∠2=180°,∠DEF=∠A,∠BED=60°.求∠ACB的度数.
解:∵∠1+∠2=180°,∠1+∠3=180°,∴∠2=∠3.
∴AB∥EF.
∴∠BDE=∠DEF.
又∵∠DEF=∠A,
∴∠BDE=∠A.
∴DE∥AC.
∴∠ACB=∠BED=60°.
5.3
平行线的性质
第4课时
相交线、平行线中角的计算的四种常见题型
第五章
相交线与平行线
1.如图,三条直线AB,CD,EF相交于同一点O.若∠AOE=2∠BOD,∠COF比∠AOE大30°,求∠AOC的度数.
1
题型
利用余角、平角、对顶角转换求角
解:设∠AOC=x°,则∠BOD=∠AOC=x°.
∴∠AOE=2∠BOD=2x°,
∠COF=∠AOE+30°=2x°+30°.
∵∠AOE+∠AOC+∠COF=180°,
∴2x+x+2x+30=180,解得x=30.
∴∠AOC=30°.
2.已知OA⊥OB,OC⊥OD.
(1)如图①,若∠BOC=50°,求∠AOD的度数;
(2)如图②,若∠BOC=60°,求∠AOD的度数;
2
题型
利用垂线求角
(3)根据(1)(2)的结果猜想∠AOD与∠BOC有怎样的关系,并根据图①说明理由;
(4)如图②,若∠BOC∶∠AOD=7∶29,求∠BOC和∠AOD的度数.
解:(1)∵OA⊥OB,
∴∠AOB=90°.
∴∠AOC=∠AOB-∠BOC=90°-50°=40°.
∵OC⊥OD,
∴∠COD=90°.
∴∠AOD=∠AOC+∠COD=40°+90°=130°.
(2)∵OA⊥OB,
∴∠AOB=90°.
∵OC⊥OD,
∴∠COD=90°.
∴∠AOD=360°-∠AOB-∠BOC-∠COD=
360°-90°-60°-90°=120°.
(3)∠AOD与∠BOC互补.理由如下:
∵OA⊥OB,∴∠AOB=90°.
∴∠AOC=∠AOB-∠BOC=90°-∠BOC.
∵OC⊥OD,∴∠COD=90°.
∴∠AOD=∠AOC+∠COD=90°-∠BOC+90°=180°-∠BOC.
∴∠AOD+∠BOC=180°,即∠AOD与∠BOC互补.
(4)由(3)可知∠BOC+∠AOD=180°,
∴∠BOC=
×180°=35°,
∠AOD=180°-∠BOC=145°.
3.(中考·重庆)如图,AB∥CD,三角形EFG的顶点F,G分别落在直线AB,CD上,GE交AB于点H,GE平分∠FGD.若∠EFG=90°,∠E=35°,求∠EFB的度数.
3
题型
直接利用平行线的性质求角
解:∵在三角形EFG中,∠EFG=90°,∠E=35°,
∴∠EGF=180°-90°-35°=55°.
∵GE平分∠FGD,
∴∠EGF=∠EGD=55°.
∵AB∥CD,
∴∠EHB=∠EGD=55°.
又∵∠EHB=180°-∠AHE=∠EFB+∠E,
∴∠EFB=∠EHB-∠E=55°-35°=20°.
4.(中考·宿迁)如图,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( )
A.80°
B.85°
C.95°
D.100°
4
题型
综合应用平行线的性质与判定求角
B
5.如图,∠1+∠2=180°,∠DEF=∠A,∠BED=60°.求∠ACB的度数.
解:∵∠1+∠2=180°,∠1+∠3=180°,∴∠2=∠3.
∴AB∥EF.
∴∠BDE=∠DEF.
又∵∠DEF=∠A,
∴∠BDE=∠A.
∴DE∥AC.
∴∠ACB=∠BED=60°.
