5.1 任意角和弧度制(共28张PPT)
文档属性
| 名称 | 5.1 任意角和弧度制(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 13:07:10 | ||
图片预览






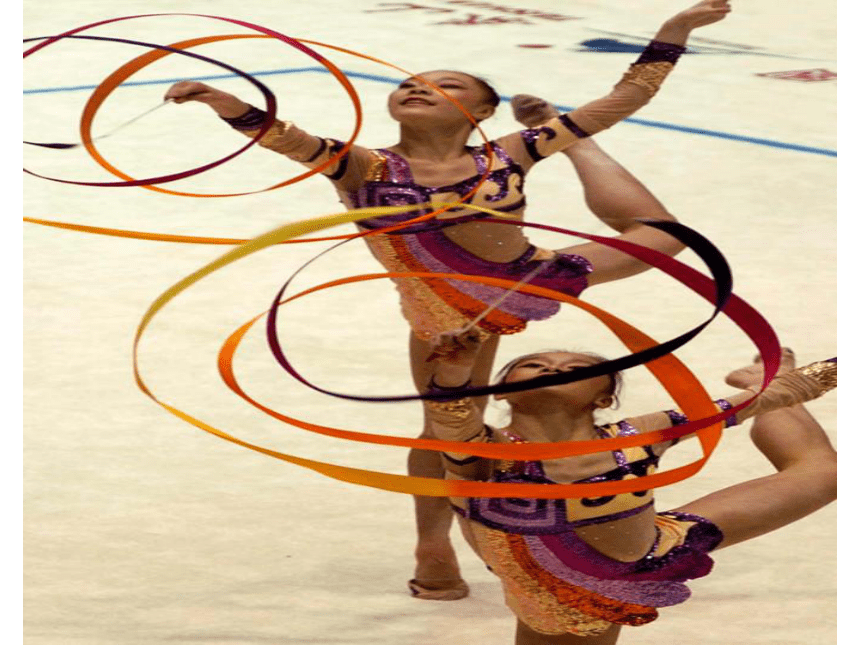
文档简介
(共28张PPT)
新
课
引
入
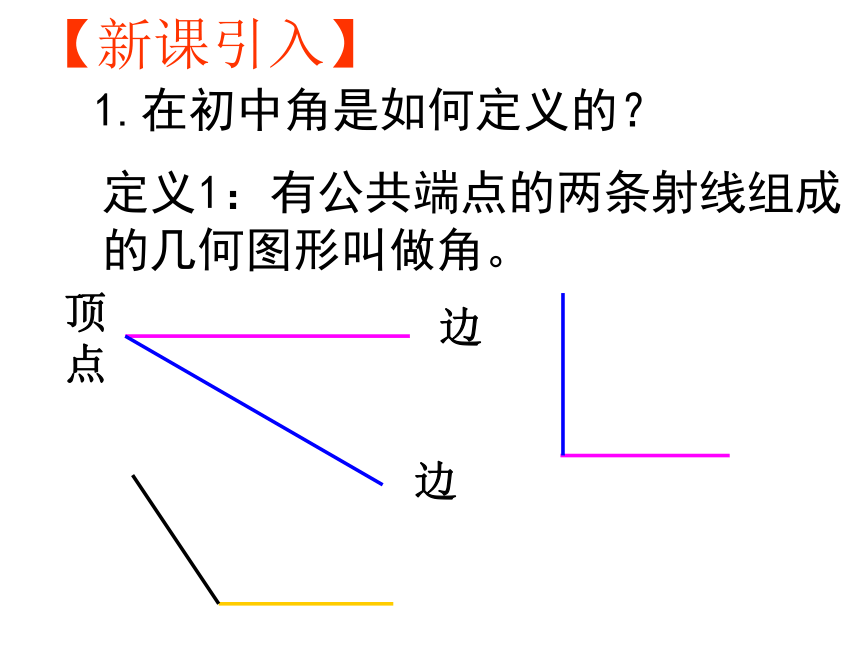
1.在初中角是如何定义的?
定义1:有公共端点的两条射线组成的几何图形叫做角。
顶点
边
边
【新课引入】
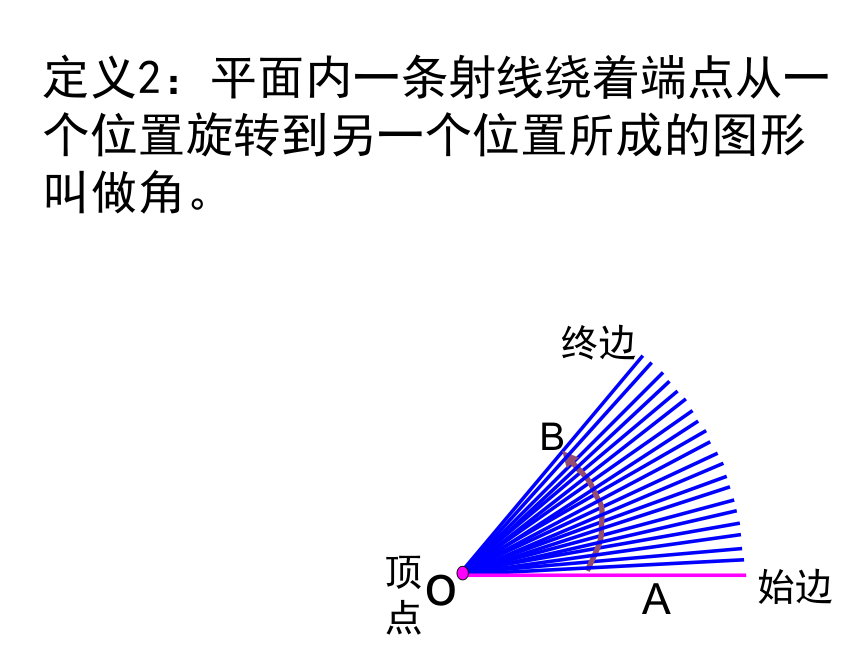
o
A
B
始边
终边
顶点
定义2:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角。
2.生活中很多实例会不在
[00
,3600
]
这个范围内。
如:
体操运动员转体720?,跳水运动员向内、向外转体1080?
跳水比赛
转体三周半指的是多少度?
这些例子所提到的角不仅不在范围[00
,3600
]
内,而且方向不同,有必要将角的概念推广到任意角,想想用什么办法才能推广到任意角?
运
动
3.过去我们学习了0°~360°范围的角,但在实际问题中还会遇到其他角.如在体操、花样滑冰、跳台跳水等比赛中,常常听到“转体10800”、“转体12600”这样的解说.再如钟表的指针、拧动螺丝的扳手、机器上的轮盘等,它们按照不同方向旋转所成的角,不全是0°~3600范围内的角.因此,仅有0°~360°范围内的角是不够的,我们必须将角的概念进行推广.
知识探究(一):角的概念的推广
画图表示一个大小一定的角,先画一条射线作为角的始边,再由角的正负确定角的旋转方向,再由角的绝对值大小确定角的旋转量,画出角的终边,并用带箭头的螺旋线加以标注.
β
B2
γ
A
B1
α
O
演示角
演示
知识探究(二):象限角
x
o
y
-50°
x
y
o
x
y
o
210°
-450°
x
y
o
405°
x
y
o
-200°
x
y
o
练习(口答):在直角坐标系中,判断下列各角是第几象限的角?
⑴
60°;⑵
120°;
⑶
240°;
⑷
300°;⑸
420°;⑹
480°;
演示
x
y
o
知识探究(三):终边相同的角
x
y
o
300
-330o
390o
300
思考2:这些角与30°角在数量上相差多少?
。除了这些角而外还有哪些角与30°角终边相同?
相差360o的整数倍
理论迁移
例1
在0°~360°范围内,找出与-950°12′角终边相同的角,并判定它是第几象限角.
小结
1、角的定义
2、任意角的概念
3、象限角
4、
终边与
角α相同的角
新
课
引
入
1.在初中角是如何定义的?
定义1:有公共端点的两条射线组成的几何图形叫做角。
顶点
边
边
【新课引入】
o
A
B
始边
终边
顶点
定义2:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角。
2.生活中很多实例会不在
[00
,3600
]
这个范围内。
如:
体操运动员转体720?,跳水运动员向内、向外转体1080?
跳水比赛
转体三周半指的是多少度?
这些例子所提到的角不仅不在范围[00
,3600
]
内,而且方向不同,有必要将角的概念推广到任意角,想想用什么办法才能推广到任意角?
运
动
3.过去我们学习了0°~360°范围的角,但在实际问题中还会遇到其他角.如在体操、花样滑冰、跳台跳水等比赛中,常常听到“转体10800”、“转体12600”这样的解说.再如钟表的指针、拧动螺丝的扳手、机器上的轮盘等,它们按照不同方向旋转所成的角,不全是0°~3600范围内的角.因此,仅有0°~360°范围内的角是不够的,我们必须将角的概念进行推广.
知识探究(一):角的概念的推广
画图表示一个大小一定的角,先画一条射线作为角的始边,再由角的正负确定角的旋转方向,再由角的绝对值大小确定角的旋转量,画出角的终边,并用带箭头的螺旋线加以标注.
β
B2
γ
A
B1
α
O
演示角
演示
知识探究(二):象限角
x
o
y
-50°
x
y
o
x
y
o
210°
-450°
x
y
o
405°
x
y
o
-200°
x
y
o
练习(口答):在直角坐标系中,判断下列各角是第几象限的角?
⑴
60°;⑵
120°;
⑶
240°;
⑷
300°;⑸
420°;⑹
480°;
演示
x
y
o
知识探究(三):终边相同的角
x
y
o
300
-330o
390o
300
思考2:这些角与30°角在数量上相差多少?
。除了这些角而外还有哪些角与30°角终边相同?
相差360o的整数倍
理论迁移
例1
在0°~360°范围内,找出与-950°12′角终边相同的角,并判定它是第几象限角.
小结
1、角的定义
2、任意角的概念
3、象限角
4、
终边与
角α相同的角
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
