2020-2021学年苏科版九年级数学上册第1章 一元二次方程复习课(word版含答案)
文档属性
| 名称 | 2020-2021学年苏科版九年级数学上册第1章 一元二次方程复习课(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 897.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-11 00:00:00 | ||
图片预览



文档简介
第1章
一元二次方程复习课
一、选择题(共10小题;共50分)
1.
若关于
的方程
的一个实数根的倒数恰是它本身,则
的值是
A.
B.
C.
或
D.
2.
若关于
的一元二次方程的两个根分别为
,,则这个方程可以是
A.
B.
C.
D.
3.
当我们解一元二次方程
时,可以运用因式分解法,将此方程化为
,从而得到两个一元一次方程:
或
,进而得到原方程的解为
,.这种解法体现的数学思想是
A.
转化思想
B.
函数思想
C.
数形结合思想
D.
公理化思想
4.
用配方法解一元二次方程
时,下列变形正确的是
A.
B.
C.
D.
5.
一元二次方程
的根的情况是
A.
有两个不相等的实数根
B.
有两个相等的实数根
C.
只有一个实数根
D.
没有实数根
6.
若关于
的一元二次方程
没有实数根,则一次函数
的图象不经过
A.
第四象限
B.
第三象限
C.
第二象限
D.
第一象限
7.
用配方法解一元二次方程
,此方程可变形为
A.
B.
C.
D.
8.
关于
的一元二次方程
有两个相等的实数根,则
A.
B.
C.
D.
9.
若关于
的一元二次方程
有两个不相等的实数根,则
的取值范围是
A.
B.
C.
且
D.
且
10.
若
是关于
的一元二次方程
的根,则根的判别式
和完全平方式
的大小关系是
A.
B.
C.
D.
无法确定
二、填空题(共10小题;共40分)
11.
已知一元二次方程
有两个相等的实数根,则
的值为
?.
12.
解一元二次方程
时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程:
?.
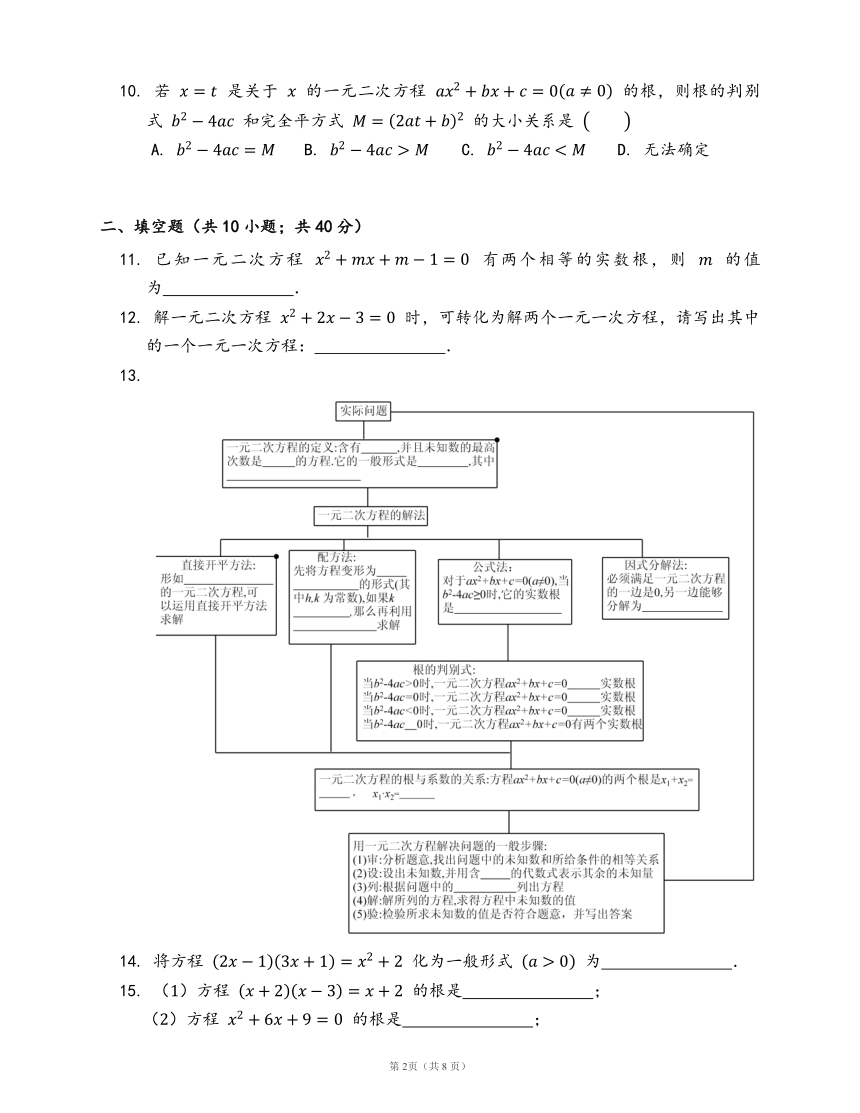
13.
14.
将方程
化为一般形式
为
?.
15.
()方程
的根是
?;
()方程
的根是
?;
16.
设一元二次方程
的两根分别是
,,则
?.
17.
已知等腰三角形的一边长为
,另一边长为方程
的根,则该等腰三角形的周长为
?.
18.
若关于
的一元二次方程
的两个实数根分别是
,,则
?.
19.
已知关于
的一元二次方程
的两个实数根分别为
,.若
,则
的值为
?.
20.
关于
的方程
有实数根,则
的取值范围是
?.
三、解答题(共8小题;共60分)
21.
用适当的方法解下列方程:
(1);
(2);
(3).
22.
已知关于
的方程
.
(1)求证:方程总有两个不相等的实数根;
(2)已知方程的一个根为
,求代数式
的值.
23.
用适当的方法解下列方程:
(1)
(2);
(3).
24.
先化简,再求值:,其中
满足方程
.
25.
在直角墙角
(,且
,
长度不限)中,要砌
米长的墙,与直角墙角
围成地面为矩形的储仓,且矩形地面
的面积为
平方米.
(1)求矩形地面的长;
(2)有规格为
和
(单位:米)的地板砖单价分别为
元和
元,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
26.
某汽车销售公司六月份销售某厂家的汽车,在一定范围内,每辆汽车的进价与销售量有如下关系:若当月仅售出
辆汽车,则该辆汽车的进价为
万元,每多售出
辆,所有售出的汽车每辆的进价均降低
万元.月底厂家根据销售量一次性返利给销售公司,销售
辆以内(含
辆),每辆返利
万元;销售
辆以上,每辆返利
万元.
(1)若该汽车销售公司当月销售
辆汽车,则每辆汽车的进价为
?
万元;
(2)若每辆汽车的售价为
万元,该汽车销售公司计划当月盈利
万元,则需要销售多少辆汽车(盈利
销售利润
返利)?
27.
为了经济发展的需要,某市
年投入科研经费
万元,
年投入科研经费
万元.
(1)求
至
年该市投入科研经费的年平均增长率;
(2)根据目前经济发展的实际情况,该市计划
年投入的科研经费比
年有所增加,但年增长率不超过
,假定该市计划
年投入的科研经费为
万元,请求出
的取值范围.
28.
已知
,
是关于
的一元二次方程
的两个实数根.
(1)若
,求
的值;
(2)已知等腰三角形
的一边长为
,若
,
恰好是
的另外两边的长,求这个三角形的周长.
答案
第一部分
1.
C
2.
B
3.
A
4.
D
5.
A
6.
D
7.
A
8.
B
9.
C
10.
A
第二部分
11.
12.
(或
)
13.
一个未知数,,,,,
是常数,,(,
为常数,),,,直接开平方法,,两个一次因式的乘积,有两个不相等的,有两个相等的,没有,,,,未知数,相等关系
14.
15.
,,
16.
17.
或
或
18.
19.
或
20.
第三部分
21.
(1)
,;
??????(2)
,;
??????(3)
,.
22.
(1)
由题意,得
,
方程总有两个不相等的实数根.
??????(2)
把
代入方程中,得到
,
或
.
,
把
代入,得
;把
代入,得
.
原代数式的值为
.
23.
(1)
,.
??????(2)
,.
??????(3)
,.
24.
.
解方程
,得
,.
使原式有意义的是
.
.
25.
(1)
设矩形地面的长是
.
由题意,得
解得
,
矩形地面的长是
米.
??????(2)
规格为
所需的费用:(元),
规格为
所需的费用:(元).
,
采用规格为
的地板砖费用较少.
26.
(1)
??????(2)
设需要销售
辆汽车.
①当销售
辆以内(含
辆)时,根据题意,得
解得
当销售
辆汽车时,当月可盈利
万元;
②当销售
辆以上时,根据题意,得
解得
综上所述,当销售
辆汽车时,当月可盈利
万元.
27.
(1)
设
至
年该市投入科研经费的年平均增长率为
.
根据题意,得
解得
至
年该市投入科研经费的年平均增长率为
.
??????(2)
根据题意,得
解得
又
该市计划
年投入的科研经费比
年有所增加,
的取值范围为
.
28.
(1)
,
是关于
的一元二次方程
的两个实数根,
,.
解得
,.
又
,解得
,
.
??????(2)
当
为底边长时,此时方程
有两个相等的实数根,
,解得
.
方程变为
,解得
.
,
不能构成三角形;当
为腰长时,设
,代入方程,得
,解得
,.
当
时,方程变为
,解得
,.
,
不能构成三角形.
不符合题意.
当
时,方程变为
,解得
,,此时三角形的周长为
.
综上所述,这个三角形的周长为
.
第4页(共8
页)
一元二次方程复习课
一、选择题(共10小题;共50分)
1.
若关于
的方程
的一个实数根的倒数恰是它本身,则
的值是
A.
B.
C.
或
D.
2.
若关于
的一元二次方程的两个根分别为
,,则这个方程可以是
A.
B.
C.
D.
3.
当我们解一元二次方程
时,可以运用因式分解法,将此方程化为
,从而得到两个一元一次方程:
或
,进而得到原方程的解为
,.这种解法体现的数学思想是
A.
转化思想
B.
函数思想
C.
数形结合思想
D.
公理化思想
4.
用配方法解一元二次方程
时,下列变形正确的是
A.
B.
C.
D.
5.
一元二次方程
的根的情况是
A.
有两个不相等的实数根
B.
有两个相等的实数根
C.
只有一个实数根
D.
没有实数根
6.
若关于
的一元二次方程
没有实数根,则一次函数
的图象不经过
A.
第四象限
B.
第三象限
C.
第二象限
D.
第一象限
7.
用配方法解一元二次方程
,此方程可变形为
A.
B.
C.
D.
8.
关于
的一元二次方程
有两个相等的实数根,则
A.
B.
C.
D.
9.
若关于
的一元二次方程
有两个不相等的实数根,则
的取值范围是
A.
B.
C.
且
D.
且
10.
若
是关于
的一元二次方程
的根,则根的判别式
和完全平方式
的大小关系是
A.
B.
C.
D.
无法确定
二、填空题(共10小题;共40分)
11.
已知一元二次方程
有两个相等的实数根,则
的值为
?.
12.
解一元二次方程
时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程:
?.
13.
14.
将方程
化为一般形式
为
?.
15.
()方程
的根是
?;
()方程
的根是
?;
16.
设一元二次方程
的两根分别是
,,则
?.
17.
已知等腰三角形的一边长为
,另一边长为方程
的根,则该等腰三角形的周长为
?.
18.
若关于
的一元二次方程
的两个实数根分别是
,,则
?.
19.
已知关于
的一元二次方程
的两个实数根分别为
,.若
,则
的值为
?.
20.
关于
的方程
有实数根,则
的取值范围是
?.
三、解答题(共8小题;共60分)
21.
用适当的方法解下列方程:
(1);
(2);
(3).
22.
已知关于
的方程
.
(1)求证:方程总有两个不相等的实数根;
(2)已知方程的一个根为
,求代数式
的值.
23.
用适当的方法解下列方程:
(1)
(2);
(3).
24.
先化简,再求值:,其中
满足方程
.
25.
在直角墙角
(,且
,
长度不限)中,要砌
米长的墙,与直角墙角
围成地面为矩形的储仓,且矩形地面
的面积为
平方米.
(1)求矩形地面的长;
(2)有规格为
和
(单位:米)的地板砖单价分别为
元和
元,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
26.
某汽车销售公司六月份销售某厂家的汽车,在一定范围内,每辆汽车的进价与销售量有如下关系:若当月仅售出
辆汽车,则该辆汽车的进价为
万元,每多售出
辆,所有售出的汽车每辆的进价均降低
万元.月底厂家根据销售量一次性返利给销售公司,销售
辆以内(含
辆),每辆返利
万元;销售
辆以上,每辆返利
万元.
(1)若该汽车销售公司当月销售
辆汽车,则每辆汽车的进价为
?
万元;
(2)若每辆汽车的售价为
万元,该汽车销售公司计划当月盈利
万元,则需要销售多少辆汽车(盈利
销售利润
返利)?
27.
为了经济发展的需要,某市
年投入科研经费
万元,
年投入科研经费
万元.
(1)求
至
年该市投入科研经费的年平均增长率;
(2)根据目前经济发展的实际情况,该市计划
年投入的科研经费比
年有所增加,但年增长率不超过
,假定该市计划
年投入的科研经费为
万元,请求出
的取值范围.
28.
已知
,
是关于
的一元二次方程
的两个实数根.
(1)若
,求
的值;
(2)已知等腰三角形
的一边长为
,若
,
恰好是
的另外两边的长,求这个三角形的周长.
答案
第一部分
1.
C
2.
B
3.
A
4.
D
5.
A
6.
D
7.
A
8.
B
9.
C
10.
A
第二部分
11.
12.
(或
)
13.
一个未知数,,,,,
是常数,,(,
为常数,),,,直接开平方法,,两个一次因式的乘积,有两个不相等的,有两个相等的,没有,,,,未知数,相等关系
14.
15.
,,
16.
17.
或
或
18.
19.
或
20.
第三部分
21.
(1)
,;
??????(2)
,;
??????(3)
,.
22.
(1)
由题意,得
,
方程总有两个不相等的实数根.
??????(2)
把
代入方程中,得到
,
或
.
,
把
代入,得
;把
代入,得
.
原代数式的值为
.
23.
(1)
,.
??????(2)
,.
??????(3)
,.
24.
.
解方程
,得
,.
使原式有意义的是
.
.
25.
(1)
设矩形地面的长是
.
由题意,得
解得
,
矩形地面的长是
米.
??????(2)
规格为
所需的费用:(元),
规格为
所需的费用:(元).
,
采用规格为
的地板砖费用较少.
26.
(1)
??????(2)
设需要销售
辆汽车.
①当销售
辆以内(含
辆)时,根据题意,得
解得
当销售
辆汽车时,当月可盈利
万元;
②当销售
辆以上时,根据题意,得
解得
综上所述,当销售
辆汽车时,当月可盈利
万元.
27.
(1)
设
至
年该市投入科研经费的年平均增长率为
.
根据题意,得
解得
至
年该市投入科研经费的年平均增长率为
.
??????(2)
根据题意,得
解得
又
该市计划
年投入的科研经费比
年有所增加,
的取值范围为
.
28.
(1)
,
是关于
的一元二次方程
的两个实数根,
,.
解得
,.
又
,解得
,
.
??????(2)
当
为底边长时,此时方程
有两个相等的实数根,
,解得
.
方程变为
,解得
.
,
不能构成三角形;当
为腰长时,设
,代入方程,得
,解得
,.
当
时,方程变为
,解得
,.
,
不能构成三角形.
不符合题意.
当
时,方程变为
,解得
,,此时三角形的周长为
.
综上所述,这个三角形的周长为
.
第4页(共8
页)
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
