人教版九年级上册数学学案:22.1.3二次函数y=a(x—h)2+k 的图象含答案
文档属性
| 名称 | 人教版九年级上册数学学案:22.1.3二次函数y=a(x—h)2+k 的图象含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 99.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览

文档简介
课题:22.1.3二次函数的图象
一、学习目标
1.巩固复习二次函数的图象的特点.
2.应用所学的二次函数的知识解决简单的实际问题.
3.培养学学生在生活中应用数学的意识.
二、教材导学
通过前面学习了二次函数的有关知识,你能够解决下列问题吗?
1、抛物线的顶点坐标是 ,对称轴是直线 ,它的开口向 ,在对称轴的左侧,即当x< 时,y随x的增大而 ;在对称轴的右侧,即当x> 时,y随x的增大而 ;当x= 时,y的值最
,最 值是 .
2、抛物线向右平移1个单位,再向下平移2个单位,所得到的抛物线是
.
3、抛物线可以通过将抛物线y=
向 平移____ 个单位、再向 平移 个单位得到.
4、抛物线关于x轴对称的抛物线的解析式为_______.
三、引领学习
知识点1:应用所学的二次函数的知识解决简单的实际问题
例4
要修建一个圆形喷水池,在池中心竖直安放一根水管,在水管的顶端安一个喷水头,使喷出的抛物线水注与池中心的水平距离为1m处达到最高,高度为3m,水注落地处离池中心3m,水管应多长.
分析:(1)抛物线的顶点在什么位置?
(2)如何建立坐标系?此时顶点的坐标是什么?还知道哪些点的坐标?
(3)求水管的长实质是求什么?
解法一:如图,建立坐标系,点(1,3)是图中这段抛物线的顶点,因此可以设抛物线的解析式为
(0≤x≤3)
请完成接下来的解法.
你还有其他的解法吗?
温馨提示:可以考虑其他的建立坐标系的方法
知识点2:培养学学生在生活中应用数学的意识.
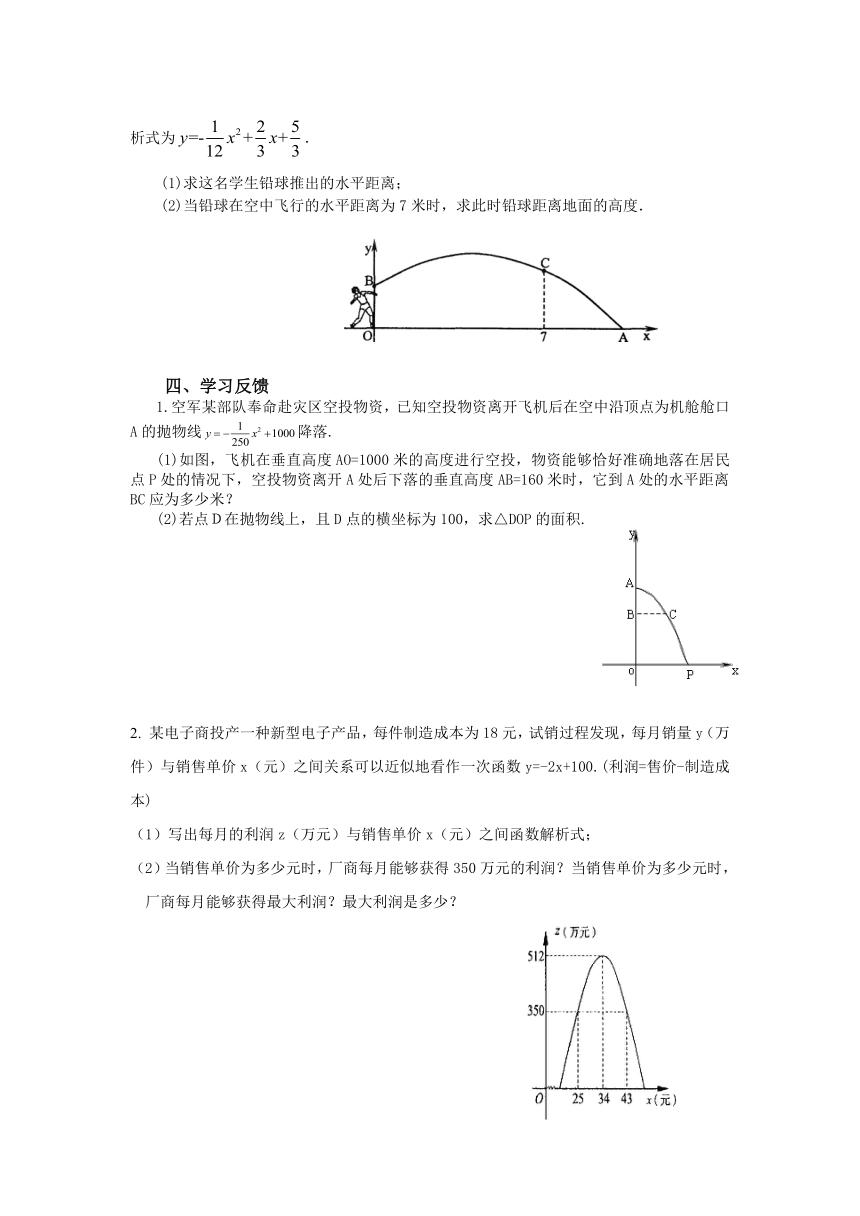
如图,是一学生投掷铅球时,铅球行进的高度y(m)与水平距离x(m)的函数图象,其解析式为.
(1)求这名学生铅球推出的水平距离;
(2)当铅球在空中飞行的水平距离为7米时,求此时铅球距离地面的高度.
四、学习反馈
1.空军某部队奉命赴灾区空投物资,已知空投物资离开飞机后在空中沿顶点为机舱舱口A的抛物线降落.
(1)如图,飞机在垂直高度AO=1000米的高度进行空投,物资能够恰好准确地落在居民点P处的情况下,空投物资离开A处后下落的垂直高度AB=160米时,它到A处的水平距离BC应为多少米?
(2)若点D在抛物线上,且D点的横坐标为100,求△DOP的面积.
2.
某电子商投产一种新型电子产品,每件制造成本为18元,试销过程发现,每月销量y(万件)与销售单价x(元)之间关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间函数解析式;
(2)当销售单价为多少元时,厂商每月能够获得350万元的利润?当销售单价为多少元时,厂商每月能够获得最大利润?最大利润是多少?
五、作业
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED距离是11米,以ED所在的直线为x轴,抛物线的对称轴y轴建立平面直角坐标系,
(1)求抛物线的解析式;
(2)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系h=- (0≤t≤40)
且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
二次函数的图象答案
二、教材导学
1、(-4,-7)
直线x=-4
上
-4
减小
-4
增大
-4
小
小-7
2、
3、
左
2
上
4
4、
三、引领学习
知识点2(1)在y=-中,当y=0,得-=0解得,(舍去),∴这名学生铅球推出的水平距离距离是10m.
(2)在y=-中,当x=7,得y=-=∴当铅球在空中飞行的水平距离为7米时,此时铅球距离地面的高度为米.
四、1、(1)由题意得A(0,1000),C(200,840).代入,得,
解得(舍去),C(200,840)∴BC=200(2)过D作DH⊥x轴于H,当时,,解得(舍去),x=100时,y=960,∴=240000.
2、解:(1)z=(x-18)y=(x-18)(-2x+100)
.
∴z与x之间的函数解析式为.
(2)由z=350,得350=,
解此方程,得.∴销售单价应定为25元或43元.把z配方,得z.因此,当销售单价为34元时,厂商每月能够获得最大利润,最大利润是512元.
五、(1)设抛物线的为y=ax2+11,由题意得B(8,8),∴64a+11=8,解得a=﹣,∴y=﹣x2+11;(2)水面到顶点C的距离不大于5米时,即水面与河底ED的距离h至多为6,∴6=﹣(t﹣19)2+8,解得t1=35,t2=3,∴35﹣3=32(小时).
一、学习目标
1.巩固复习二次函数的图象的特点.
2.应用所学的二次函数的知识解决简单的实际问题.
3.培养学学生在生活中应用数学的意识.
二、教材导学
通过前面学习了二次函数的有关知识,你能够解决下列问题吗?
1、抛物线的顶点坐标是 ,对称轴是直线 ,它的开口向 ,在对称轴的左侧,即当x< 时,y随x的增大而 ;在对称轴的右侧,即当x> 时,y随x的增大而 ;当x= 时,y的值最
,最 值是 .
2、抛物线向右平移1个单位,再向下平移2个单位,所得到的抛物线是
.
3、抛物线可以通过将抛物线y=
向 平移____ 个单位、再向 平移 个单位得到.
4、抛物线关于x轴对称的抛物线的解析式为_______.
三、引领学习
知识点1:应用所学的二次函数的知识解决简单的实际问题
例4
要修建一个圆形喷水池,在池中心竖直安放一根水管,在水管的顶端安一个喷水头,使喷出的抛物线水注与池中心的水平距离为1m处达到最高,高度为3m,水注落地处离池中心3m,水管应多长.
分析:(1)抛物线的顶点在什么位置?
(2)如何建立坐标系?此时顶点的坐标是什么?还知道哪些点的坐标?
(3)求水管的长实质是求什么?
解法一:如图,建立坐标系,点(1,3)是图中这段抛物线的顶点,因此可以设抛物线的解析式为
(0≤x≤3)
请完成接下来的解法.
你还有其他的解法吗?
温馨提示:可以考虑其他的建立坐标系的方法
知识点2:培养学学生在生活中应用数学的意识.
如图,是一学生投掷铅球时,铅球行进的高度y(m)与水平距离x(m)的函数图象,其解析式为.
(1)求这名学生铅球推出的水平距离;
(2)当铅球在空中飞行的水平距离为7米时,求此时铅球距离地面的高度.
四、学习反馈
1.空军某部队奉命赴灾区空投物资,已知空投物资离开飞机后在空中沿顶点为机舱舱口A的抛物线降落.
(1)如图,飞机在垂直高度AO=1000米的高度进行空投,物资能够恰好准确地落在居民点P处的情况下,空投物资离开A处后下落的垂直高度AB=160米时,它到A处的水平距离BC应为多少米?
(2)若点D在抛物线上,且D点的横坐标为100,求△DOP的面积.
2.
某电子商投产一种新型电子产品,每件制造成本为18元,试销过程发现,每月销量y(万件)与销售单价x(元)之间关系可以近似地看作一次函数y=-2x+100.(利润=售价-制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间函数解析式;
(2)当销售单价为多少元时,厂商每月能够获得350万元的利润?当销售单价为多少元时,厂商每月能够获得最大利润?最大利润是多少?
五、作业
如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16米,AE=8米,抛物线的顶点C到ED距离是11米,以ED所在的直线为x轴,抛物线的对称轴y轴建立平面直角坐标系,
(1)求抛物线的解析式;
(2)已知从某时刻开始的40小时内,水面与河底ED的距离h(单位:米)随时间t(单位:时)的变化满足函数关系h=- (0≤t≤40)
且当水面到顶点C的距离不大于5米时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
二次函数的图象答案
二、教材导学
1、(-4,-7)
直线x=-4
上
-4
减小
-4
增大
-4
小
小-7
2、
3、
左
2
上
4
4、
三、引领学习
知识点2(1)在y=-中,当y=0,得-=0解得,(舍去),∴这名学生铅球推出的水平距离距离是10m.
(2)在y=-中,当x=7,得y=-=∴当铅球在空中飞行的水平距离为7米时,此时铅球距离地面的高度为米.
四、1、(1)由题意得A(0,1000),C(200,840).代入,得,
解得(舍去),C(200,840)∴BC=200(2)过D作DH⊥x轴于H,当时,,解得(舍去),x=100时,y=960,∴=240000.
2、解:(1)z=(x-18)y=(x-18)(-2x+100)
.
∴z与x之间的函数解析式为.
(2)由z=350,得350=,
解此方程,得.∴销售单价应定为25元或43元.把z配方,得z.因此,当销售单价为34元时,厂商每月能够获得最大利润,最大利润是512元.
五、(1)设抛物线的为y=ax2+11,由题意得B(8,8),∴64a+11=8,解得a=﹣,∴y=﹣x2+11;(2)水面到顶点C的距离不大于5米时,即水面与河底ED的距离h至多为6,∴6=﹣(t﹣19)2+8,解得t1=35,t2=3,∴35﹣3=32(小时).
同课章节目录
