人教版九年级上册数学学案:22.1.4 二次函数y=ax2+bx+c的图象(Word版 含答案)
文档属性
| 名称 | 人教版九年级上册数学学案:22.1.4 二次函数y=ax2+bx+c的图象(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 70.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 12:12:06 | ||
图片预览

文档简介
课题:
22.1.4
二次函数y=ax2+bx+c的图象
一.学习目标
1、使学生掌握用描点法画出函数y=ax2+bx+c的图象;
2、使学生掌握用图象或通过配方确定抛物线的开口方向、对称轴和顶点坐标。
3、让学生经历探索二次函数y=ax2+bx+c的图象的开口方向、对称轴和顶点坐标以及性质的过程,理解二次函数y=ax2+bx+c的性质。;
二.教材导学
(一)知识回顾:
1、抛物线的顶点坐标是
;对称轴是直线
;当=
时有最
值是
;当
时,随的增大而增大;当
时,随的增大而减小。
2.
二次函数解析式中,很容易确定抛物线的顶点坐标为
,所以这种形式被称作二次函数的顶点式。
(二)、自主学习:
知识点:用顶点坐标和对称轴公式也可以直接求出抛物线的顶点坐标和对称轴,这种方法叫做公式法。
(1)你能直接说出函数
的图像的对称轴和顶点坐标吗?
(2)你有办法解决问题(1)吗?
解:
的顶点坐标是
,对称轴是
.
(3)像这样我们可以把一个一般形式的二次函数用
的方法转化为
式从而直接得到它的图像性质.
(4)用配方法把下列二次函数化成顶点式:
①
②
(5).顶点坐标公式的推导
y=ax2+bx+c=a(x2+x)+c
=a[x2+x+()2-()2]+c
=a[x2+x+()2]+c-=a(x+)2+
(6)用顶点坐标和对称轴公式也可以直接求出抛物线的顶点坐标和对称轴,这种方法叫做公式法。
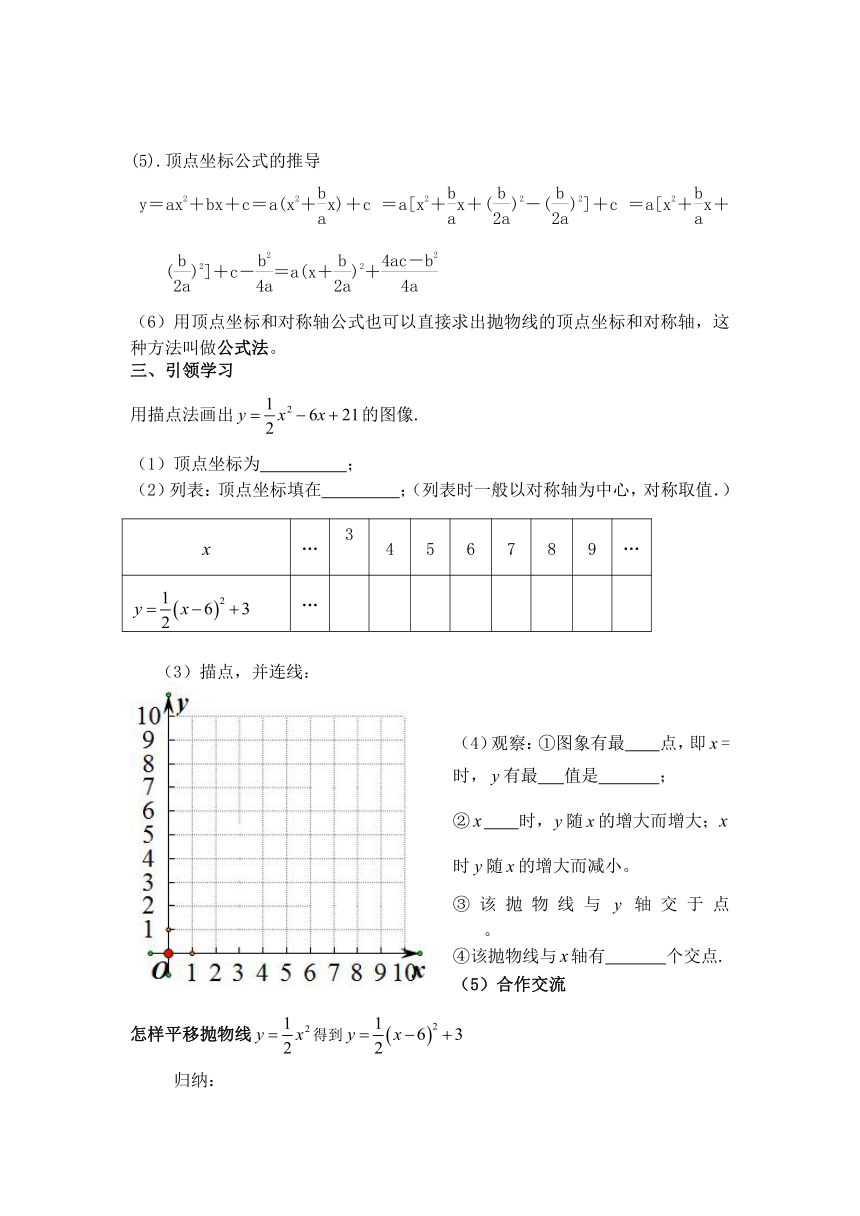
三、引领学习
用描点法画出的图像.
(1)顶点坐标为
;
(2)列表:顶点坐标填在
;(列表时一般以对称轴为中心,对称取值.)
…
3
4
5
6
7
8
9
…
…
(3)描点,并连线:
(4)观察:①图象有最
点,即=
时,有最
值是
;
②
时,随的增大而增大;
时随的增大而减小。
③该抛物线与轴交于点
。
④该抛物线与轴有
个交点.
(5)合作交流
怎样平移抛物线得到
归纳:
1.一般地,我们用配方法求抛物线
y=ax2+bx+c(a≠0)的顶点与对称轴。
y=ax2+bx+c
=a(x+)2+
因此,当a>0时,开口向上,当a<0时,开口向下。对称轴是x=-,顶点坐标是(-,)
四、学习反馈:
1.填空:
(1)抛物线y=x2-2x+2的顶点坐标是_______;
(2)抛物线y=2x2-2x-的开口_______,对称轴是_______;
(3)抛物线y=-2x2-4x+8的开口_______,顶点坐标是_______;
(4)抛物线y=-x2+2x+4的对称轴是_______;
2.画出函数y=2x2-3x的图象,说明这个函数具有哪些性质。
3.用配方法求二次函数y=-2x2-4x+1的顶点坐标.
4.用两种方法求二次函数y=x2+2x的顶点坐标.
5.用顶点坐标公式和配方法求二次函数y=x2-2-1的顶点坐标
6.写出下列抛物线的开口方向、对称轴及顶点坐标。
(1)
(2)
(3)
(4)
22.1.4
二次函数y=ax2+bx+c的图象
参考答案:
教材导学
(1)知识回顾
1、(-3,-1),x=-3,-3,小,-1,>-3,<-3.
2、(h,k)。
(2)自主学习②
解:
配方得:
(-1,1),x=-1
③配方,。④
引领学习
(1)(6,3),(2)中间7.5,5,3.5,03,5,5,7.5.
(3)略(4)①低,6,小,3.
②>6,
<6.③(0,21)④1.(5)把抛物线向右平移6个单位,再向上平移3个单位。
学习反馈
1、(1)(1,1),(2)向上,x=。(3)向下,(1,6)。(4)x=2.
2,、略。3、。4、(-1,-1)。5、(2,-4)。
6、(1)开口向上,对称轴:x=-3,顶点坐标(,-)。
(2)开口向下,对称轴:x=-1,顶点坐标(-1,1)。
(3)开口向下,对称轴:x=2,顶点坐标(2,0)。
(4)开口向上,对称轴:x=4,顶点坐标(4,-5)。
22.1.4
二次函数y=ax2+bx+c的图象
一.学习目标
1、使学生掌握用描点法画出函数y=ax2+bx+c的图象;
2、使学生掌握用图象或通过配方确定抛物线的开口方向、对称轴和顶点坐标。
3、让学生经历探索二次函数y=ax2+bx+c的图象的开口方向、对称轴和顶点坐标以及性质的过程,理解二次函数y=ax2+bx+c的性质。;
二.教材导学
(一)知识回顾:
1、抛物线的顶点坐标是
;对称轴是直线
;当=
时有最
值是
;当
时,随的增大而增大;当
时,随的增大而减小。
2.
二次函数解析式中,很容易确定抛物线的顶点坐标为
,所以这种形式被称作二次函数的顶点式。
(二)、自主学习:
知识点:用顶点坐标和对称轴公式也可以直接求出抛物线的顶点坐标和对称轴,这种方法叫做公式法。
(1)你能直接说出函数
的图像的对称轴和顶点坐标吗?
(2)你有办法解决问题(1)吗?
解:
的顶点坐标是
,对称轴是
.
(3)像这样我们可以把一个一般形式的二次函数用
的方法转化为
式从而直接得到它的图像性质.
(4)用配方法把下列二次函数化成顶点式:
①
②
(5).顶点坐标公式的推导
y=ax2+bx+c=a(x2+x)+c
=a[x2+x+()2-()2]+c
=a[x2+x+()2]+c-=a(x+)2+
(6)用顶点坐标和对称轴公式也可以直接求出抛物线的顶点坐标和对称轴,这种方法叫做公式法。
三、引领学习
用描点法画出的图像.
(1)顶点坐标为
;
(2)列表:顶点坐标填在
;(列表时一般以对称轴为中心,对称取值.)
…
3
4
5
6
7
8
9
…
…
(3)描点,并连线:
(4)观察:①图象有最
点,即=
时,有最
值是
;
②
时,随的增大而增大;
时随的增大而减小。
③该抛物线与轴交于点
。
④该抛物线与轴有
个交点.
(5)合作交流
怎样平移抛物线得到
归纳:
1.一般地,我们用配方法求抛物线
y=ax2+bx+c(a≠0)的顶点与对称轴。
y=ax2+bx+c
=a(x+)2+
因此,当a>0时,开口向上,当a<0时,开口向下。对称轴是x=-,顶点坐标是(-,)
四、学习反馈:
1.填空:
(1)抛物线y=x2-2x+2的顶点坐标是_______;
(2)抛物线y=2x2-2x-的开口_______,对称轴是_______;
(3)抛物线y=-2x2-4x+8的开口_______,顶点坐标是_______;
(4)抛物线y=-x2+2x+4的对称轴是_______;
2.画出函数y=2x2-3x的图象,说明这个函数具有哪些性质。
3.用配方法求二次函数y=-2x2-4x+1的顶点坐标.
4.用两种方法求二次函数y=x2+2x的顶点坐标.
5.用顶点坐标公式和配方法求二次函数y=x2-2-1的顶点坐标
6.写出下列抛物线的开口方向、对称轴及顶点坐标。
(1)
(2)
(3)
(4)
22.1.4
二次函数y=ax2+bx+c的图象
参考答案:
教材导学
(1)知识回顾
1、(-3,-1),x=-3,-3,小,-1,>-3,<-3.
2、(h,k)。
(2)自主学习②
解:
配方得:
(-1,1),x=-1
③配方,。④
引领学习
(1)(6,3),(2)中间7.5,5,3.5,03,5,5,7.5.
(3)略(4)①低,6,小,3.
②>6,
<6.③(0,21)④1.(5)把抛物线向右平移6个单位,再向上平移3个单位。
学习反馈
1、(1)(1,1),(2)向上,x=。(3)向下,(1,6)。(4)x=2.
2,、略。3、。4、(-1,-1)。5、(2,-4)。
6、(1)开口向上,对称轴:x=-3,顶点坐标(,-)。
(2)开口向下,对称轴:x=-1,顶点坐标(-1,1)。
(3)开口向下,对称轴:x=2,顶点坐标(2,0)。
(4)开口向上,对称轴:x=4,顶点坐标(4,-5)。
同课章节目录
