人教版初中物理八年级上册6.3测量物质的密度 同步练习(含答案解析)
文档属性
| 名称 | 人教版初中物理八年级上册6.3测量物质的密度 同步练习(含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 209.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-12-12 15:11:04 | ||
图片预览



文档简介
6.3测量物质的密度
同步测试
一.选择题
1.我们在用天平和量筒测量某种液体密度时,以下操作步骤中,不必要的是( )
A.将烧杯中的部分液体倒入量筒中,测出倒入量筒中的液体的体积
B.取适量的液体倒入烧杯中,用天平测出烧杯和液体的总质量
C.用天平测出空烧杯的质量
D.用天平测出烧杯和剩余液体的总质量
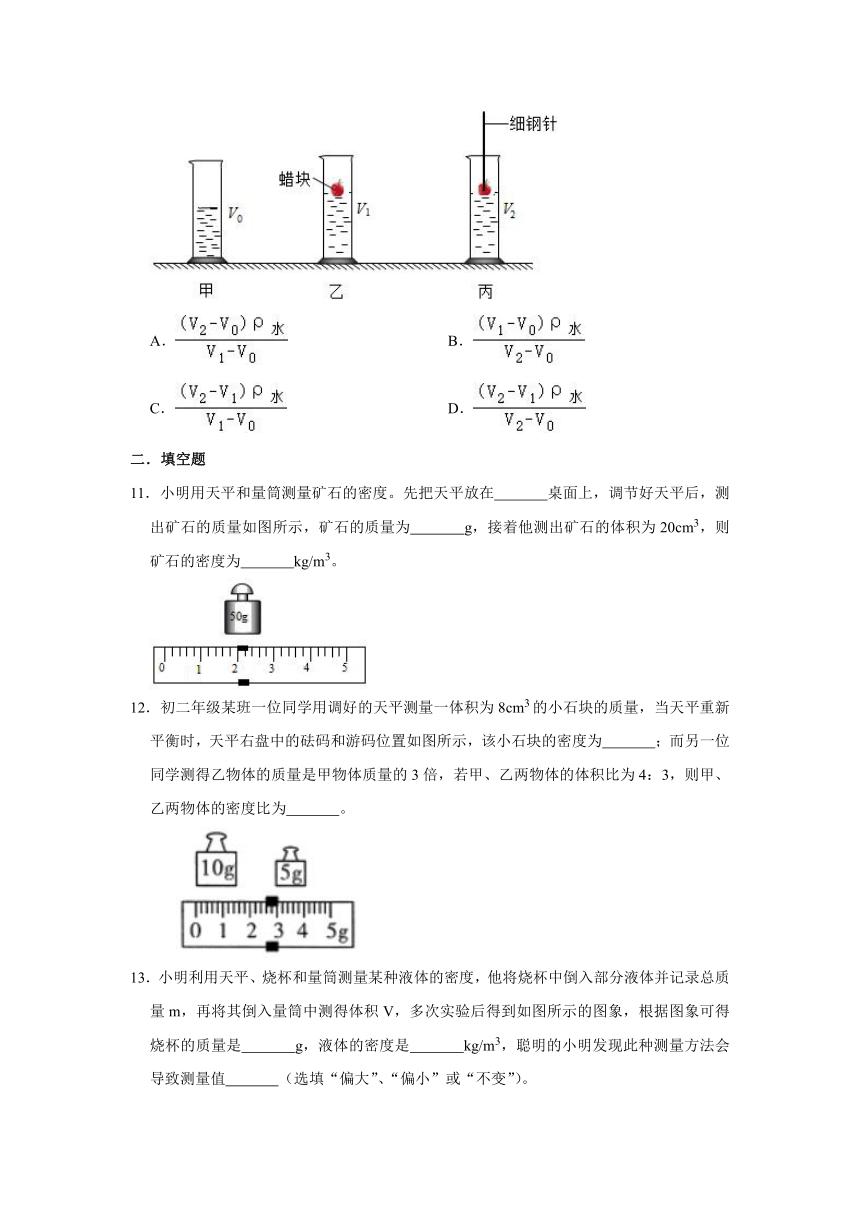
2.为了测出石块的密度,某同学先用天平测石块的质量,所加砝码和游码在标尺上的位置如图甲所示,接着用量筒和水测矿石的体积,其过程如图乙所示。下列判断错误的是( )
A.石块的质量是47.2g
B.石块的体积是18cm3
C.石块的密度是2.6×103kg/m3
D.若先测石块的体积,最终测得石块的密度会偏大
3.用密度为2.7×103kg/m3的铝制成甲、乙、丙三个大小不同的正方体。要求它们的边长分别是0.1m、0.2m和0.3m,制成后让质量检查员称出它们的质量,分别是3kg、21.6kg和54kg,质量检查员指出,有两个不合格,其中一个掺入了杂质为次品,另一个混入了空气泡为废品,则这三个正方体( )
A.甲为废品,乙为合格品,丙为次品
B.甲为合格品,乙为废品,丙为次品
C.甲为次品,乙为合格品,丙为废品
D.甲为废品,乙为次品,丙为合格品
4.某同学用托盘天平和量筒测量一小石块的密度,图甲是调节天平时的情形,图乙和图丙分别是测量石块质量和体积时的情形,下列说法中正确的是( )
A.甲图中应将平衡螺母向左调,使横梁平衡
B.乙图中测石块质量时,天平的示数是17.4g
C.由丙图量筒的示数测得石块的体积是40cm3
D.利用图中信息,可计算出石块的密度是1.72×103kg/m3
5.以下为某同学测定煤油密度的一些实验步骤,这些步骤中可省去的步骤是( )
①用天平称出空矿泉水瓶的质量m0
②在矿泉水瓶里装满水,用天平称出它们的总质量m1
③用天平称出矿泉水瓶装满煤油后的总质量m2
④用量筒测出矿泉水瓶里所盛煤油的体积V
⑤计算煤油的密度
A.①
B.②或④
C.③
D.都不能省去
6.王梦与其他三位同学先后测量同一小石块的密度,下表中数据是他们的测量结果。
学生
王梦
赵满
李明
张扬
小石块的密度
2.45g/cm3
2.52g/cm3
2.56g/cm3
2.60g/cm3
经查密度表可知,石块的密度为2.50g/cm3.则下列说法正确的是( )
A.赵满的结果可以接受,因为他的数据与2.50g/cm3最接近
B.张扬的结果不可以接受,因为他的数据与2.50g/cm3偏差最大
C.如果实验操作正确,数据真实,上述结果均有效
D.四位同学的实验都失败了,因为他们的测量值都不是2.50g/cm3
7.小明用利用托盘天平和量筒测量盐水的密度。部分操作过程如图所示,下列说法不正确的是( )
A.量筒中液体的体积是40cm3
B.盐水的密度是1.165×103kg/m3
C.如果按照B、A、C的顺序会使测量结果偏小
D.按照A、C、B顺序操作如果盘中5g砝码因生锈质量变大则测得盐水密度偏大
8.小明和同学一起做测小石块密度的实验。下表记录的是小明与其他三位同学测出的小石块密度(注:经查密度表可知,石块的密度为2.50g/cm3)下列说法正确的是( )
学生
小明
小华
小李
小张
小石块的密度g/cm3
2.45
2.52
2.56
2.54
A.四位考生的实验都失败了,因为密度表中石块的密度为2.50g/cm3
B.只有小华的数据可以接受,因为她的数据最接近密度表中的数据
C.只有小张的数据不可以接受,因为他的数据偏差最大
D.只要实验操作正确,数据真实,上述数据均有效
9.在一次课外活动中,某同学拾到一块小矿石,查阅相关资料获知该矿石的密度为2.50g/cm3.四位同学分别设计实验方案各自测得矿石的密度为ρ甲=2.48g/cm3、ρ乙=2.51g/cm3、ρ丙=2.47g/cm3,ρ丁=2.56g/cm3,则下列分析中正确的是( )
A.四位同学的测量是错误的,因为该矿石的密度值为2.50g/cm3
B.只有乙同学的测量是正确的,因为他测得的数据最接近矿石密度的真实值
C.只有丁同学的测量是错误的,因为他测得的数据与矿石密度的真实值偏差最大
D.只要实验方案合理、操作正确,数据真实,四位同学测量的数据都是有效的
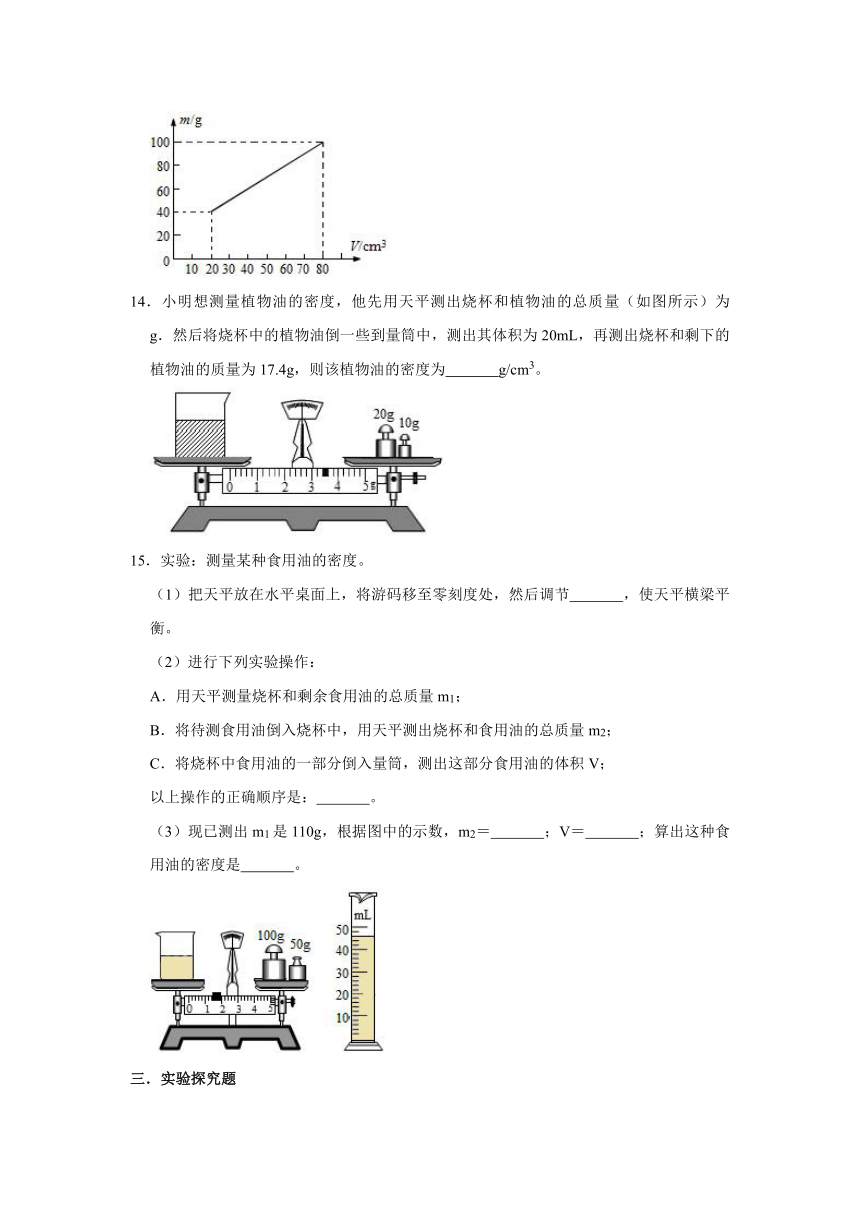
10.小亮利用细钢针、量筒和适量的水测量一个形状不规则的小蜡块的密度。小亮正确的测量过程如图甲、乙、丙所示,图中V0、V1、V2分别是量筒中水面所对应的示数。已知水的密度为ρ水,则下列四个选项中,小蜡块密度ρ蜡的表达式正确的是( )
A.
B.
C.
D.
二.填空题
11.小明用天平和量筒测量矿石的密度。先把天平放在
桌面上,调节好天平后,测出矿石的质量如图所示,矿石的质量为
g,接着他测出矿石的体积为20cm3,则矿石的密度为
kg/m3。
12.初二年级某班一位同学用调好的天平测量一体积为8cm3的小石块的质量,当天平重新平衡时,天平右盘中的砝码和游码位置如图所示,该小石块的密度为
;而另一位同学测得乙物体的质量是甲物体质量的3倍,若甲、乙两物体的体积比为4:3,则甲、乙两物体的密度比为
。
13.小明利用天平、烧杯和量筒测量某种液体的密度,他将烧杯中倒入部分液体并记录总质量m,再将其倒入量筒中测得体积V,多次实验后得到如图所示的图象,根据图象可得烧杯的质量是
g,液体的密度是
kg/m3,聪明的小明发现此种测量方法会导致测量值
(选填“偏大”、“偏小”或“不变”)。
14.小明想测量植物油的密度,他先用天平测出烧杯和植物油的总质量(如图所示)为
g.然后将烧杯中的植物油倒一些到量筒中,测出其体积为20mL,再测出烧杯和剩下的植物油的质量为17.4g,则该植物油的密度为
g/cm3。
15.实验:测量某种食用油的密度。
(1)把天平放在水平桌面上,将游码移至零刻度处,然后调节
,使天平横梁平衡。
(2)进行下列实验操作:
A.用天平测量烧杯和剩余食用油的总质量m1;
B.将待测食用油倒入烧杯中,用天平测出烧杯和食用油的总质量m2;
C.将烧杯中食用油的一部分倒入量筒,测出这部分食用油的体积V;
以上操作的正确顺序是:
。
(3)现已测出m1是110g,根据图中的示数,m2=
;V=
;算出这种食用油的密度是
。
三.实验探究题
16.小贾同学在学习了密度的测量之后,准备测量身边矿石的密度。
(1)小贾将天平放在
台面上,把游码移至标尺左端0刻线处,发现天平的指针偏向如图甲,他应将
向
调,使天平横梁平衡。
(2)调节完毕后,他使用天平测量这一小矿石的质量如图乙所示,其操作错误是:
。改正错误后,他测出了小矿石的质量如图丙为
g。
(3)在测量小矿石体积时,他首先应该将适量的水倒入量筒中,然后再将小矿石缓慢浸没在量筒中,如图丁测出小矿石的体积,根据以上测量的质量和体积算出小矿石的密度为
kg/m3;在测量小矿石体积时,如果考虑棉线的体积,则测量值
(选填“偏大”、“不变”或“偏小”)。
17.小刚在测量食用油密度的实验中,先将天平放在水平桌面上,移动游码至标尺左端“0”刻度线后指针位置如图甲所示,他随即在天平左盘中放入盛有食用油的烧杯,在右盘中加入砝码,并移动游码,使天平平衡,测得烧杯和食用油的总质量为87.8g。
(1)随后,他提起烧杯向空量筒中倒入30.0mL的食用油,再将烧杯放入天平左盘中,当右盘所加砝码和游码位置如图乙所示时,天平再次平衡,于是他计算得出食用油的密度为
kg/m3。
(2)在开始测量质量前,小刚没有调节天平平衡,这使他第一次测得的烧杯和食用油的总质量
(选填“偏大”“不变”或“偏小”),在(1)中测得的食用油密度
(选填“偏大”“不变”或“偏小”)。
18.某物理兴趣小组需要测量某樱桃酒的密度,他们利用天平和量筒进行了测量,实验过程如下:
A.用已调平衡的天平测出烧杯的质量为m1;
B.向烧杯中倒入适量的樱桃酒,测出烧杯和樱桃酒的总质量m2;
C.将烧杯中的樱桃酒全部倒入量筒中,读出量筒中樱桃酒的体积V。
(1)该小组测量樱桃酒密度的原理是:
;
(2)经讨论,该小组实验方案存在较大的误差,产生较大误差的原因是:
,改进措施时只要把实验顺序变一下即可,请你写出合理的顺序(填步骤前的字母序号):
;
(3)改进后的计算密度的公式是:(用步骤中测量量的符号表示)
;
(4)小华不小心将量筒打碎了,小明想出了一个新方案:
①将空烧杯放在天平上,测出其质量为46g;
②在烧杯中倒入适量的水,将水面的位置标记在烧杯壁上。将盛有水的烧杯放在天平上,测出其质量为116g,则烧杯中水的体积为
cm3;
③将水倒出擦干,在烧杯中倒入樱桃酒至标记处,将此烧杯放在天平上,天平平衡时,右盘中砝码质量和游码的位置如图所示,则烧杯和樱桃酒的总质量为
g;
④计算得出樱桃酒的密度为
g/cm3。
参考答案
一.选择题
1.解:测液体密度,若先测空烧杯的质量,再测烧杯和液体总质量,最后将液体倒入量筒来测体积,这种做法会因烧杯壁粘液体而使测出的体积偏小,导致算出的液体密度偏大。
为防止容器壁粘液体带来实验误差,应先测烧杯和液体总质量,再将液体倒入量筒测出体积,最后测出剩余液体和烧杯的质量,用密度公式ρ=算出液体的密度。所以本题中选项C用天平测出空烧杯的质量是不必要的。
故选:C。
2.解:
A、图甲中矿石的质量m=20g+20g+5g+1.8g=46.8g,故A错误;
B、图乙中水的体积为20cm3,水和矿石的总体积为38cm3,矿石的体积V=38cm3﹣20cm3=18cm3,故B正确;
C、矿石的密度ρ===2.6g/cm3=2.6×103kg/m3,故C正确;
D、若先测石块的体积,石块从量筒中取出会带着水,使的质量测量值偏大,则测量的密度值偏大,故D正确。
故选:A。
3.解:甲的体积:V甲=0.1m×0.1m×0.1m=0.001m3,则甲的密度:ρ甲===3×103kg/m3;
乙的体积:V乙=0.2m×0.2m×0.2m=0.008m3,则乙的密度:ρ乙===2.7×103kg/m3;
丙的体积:V丙=0.3m×0.3m×0.3m=0.027m3,则丙的密度:ρ丙===2×103kg/m3。
因为ρ乙=ρ铝,所以乙是合格品;因为ρ丙<ρ铝,所以丙是废品;因为ρ甲>ρ铝,所以甲是次品。
故选:C。
4.解:A、由图甲知,指针左偏,应将平衡螺母向右调使横梁平衡,故A错误;
B、由图乙知,标尺的分度值为0.2g,石块的质量m=10g+5g+2.2g=17.2g,故B错误,
C、由图丙知,水的体积为30mL,水和石块的总体积为40mL,
则石块的体积V=40mL﹣30mL=10mL=10cm3,故C错误;
D、石块的密度ρ===1.72g/cm3=1.72×103kg/m3,故D正确。
故选:D。
5.解:(1)为测出一定体积液体的质量,要根据矿泉水瓶的质量与煤油质量的和减去矿泉水瓶的质量,因此①不能省去;
(2)一定质量的煤油的体积可由量筒量出,或根据水的质量与密度求出其体积,所以可省去②或④,所以B正确;
(3)要根据矿泉水瓶的质量与煤油质量的和减去矿泉水瓶的质量而得出煤油的质量,因此③不能省去;
(4)由以上分析可得,D不正确。
故选:B。
6.解:在实验中,只要操作正确,数据便是真实的。
几个组数据的不同,是因为在测量过程中存在误差,所以如果实验操作正确,数据真实,上述结果均有效,故ABD错误,C正确。
故选:C。
7.解:
A、量筒的分度值为1cm3,量筒中盐水的体积为V=40cm3;故A正确;
B、在天平的标尺上,1g之间有5个小格,一个小格代表的质量是0.2g,即天平的分度值为0.2g;烧杯和盐水的总质量是m1=50g+20g+10g+2.4g=82.4g;
剩余盐水和烧杯的质量为m2=20g+10g+5g+0.8g=35.8g,
量筒中盐水的质量为m=m1﹣m2=82.4g﹣35.8g=46.6g,
盐水的密度为ρ==,=1.165g/cm3=1.165×103kg/m3;故B正确;
C、如果按照B、A、C的顺序,盐水质量准确,但是,由于一部分液体附着在烧杯壁上,倒入量筒中的盐水比实际偏小,由公式ρ=判断密度偏大,故C错误;
D、如果砝码生锈,则砝码的质量比实际值较大,所以当左盘放置1kg的物体时,右盘只需放置小于1kg的砝码即可,所以称得质量比实际质量偏小,则两次质量测量之差偏大,由公式ρ=得密度偏大,故D正确。
故选:C。
8.解:在实验中,只要操作正确,数据便是真实的。几个组数据的不同,是因为在测量过程中存在误差的原因。故ABC选项错误,D选项正确。
故选:D。
9.解:因为四位同学所测得都与真实值相差不大,只要实验方案合理、操作正确,数据真实,四位同学测量的数据都是有效的,故ABC错误,D正确。
故选:D。
10.解:
小蜡块漂浮在水面上,受到的重力等于排开水的重力,
由图甲和乙可知,小蜡块的质量等于它排开水的质量,
所以,m=m排水=(V1﹣V0)ρ水,
由甲和丙可知,小蜡块的体积为V=V2﹣V0,
所以小蜡块的密度:ρ==。
故选:B。
二.填空题
11.解:
天平使用时,应先杷天平放在水平桌面上;
由图知,天平标尺的分度值0.2g,矿石的质量:m=50g+2g=52g;
由题知,矿石的体积为20cm3,矿石的密度:ρ===2.6g/cm3=2.6×103kg/m3。
故答案为:水平;52;2.6×103。
12.解:
(1)由图知,称量标尺的分度值为0.2g,游码显示的示数为2.6g,物体的质量为:
m=10g+5g+2.6g=17.6g;
甲的密度为:
ρ甲===2.2g/cm3;
(2)由题知,m甲:m乙=1:3,V甲:V乙=4:3,
甲、乙两物体的密度:
ρ甲:ρ乙=:=×=×=1:4。
故答案为:2.2g/cm3;1:4。
13.解:由图象可知,当液体的体积由20cm3增加到80cm3时,液体的质量增加了m=100g﹣40g=60g;即60g的液体的体积为:V=80cm3﹣20cm3=60cm3;
则液体的密度为:ρ===1g/cm3=1×103kg/m3;
由图可知,当液体的体积为V'=20cm3时,总的质量为40g;
20cm3的液体的质量为:m'=ρV'=1g/cm3×20cm3=20g;
则烧杯的质量为:40g﹣20g=20g;
把烧杯中的液体全部倒入量筒中时,烧杯内的液体不可能全部倒入量筒中,烧杯内有液态的残留,会使得倒入量筒中液体的体积变小,根据ρ=可知,液体的密度偏大。
故答案为:20;1×103;偏大。
14.解:∵将砝码的质量加上游码所对应的刻度就是烧杯和植物油的总质量,
∴由图示可得烧杯和植物油的总质量为:20g+10g+3.4g=33.4g。
∵量筒内植物油的质量等于烧杯和植物油的总质量减去烧杯和剩余植物油的质量,
∴量筒内植物油的质量为:33.4g﹣17.4g=16g。
又∵测出量筒内植物油的体积为20ml,即20cm3。
∴根据密度公式ρ=得:ρ油===0.8g/cm3。
故答案为:33.4;0.8。
15.解:(1)把天平放在水平桌面上,将游码移至零刻度处,然后调节平衡螺母,使横梁平衡;
(2)测量液体密度的实验步骤为:先测出烧杯和食用油的总质量,再将一部分食用油倒入量筒读出体积,再测出烧杯和剩余食用油的总质量,
故操作的正确顺序是:BCA;
(3)图中烧杯和食用油的总质量m2=100g+50g+1.4g=151.4g,
量筒中食用油的质量m=m2﹣m1=151.4g﹣110g=41.4g,
量筒中食用油的体积V=46cm3,
食用油的密度ρ===0.9g/cm3。
故答案为:(1)平衡螺母;(2)BCA;(3)151.4g;46cm3;0.9g/cm3。
三.实验探究题
16.解:(1)天平在使用,应放在水平水平台面上;使用前调平衡,将游码用镊子拨动到标尺左端零刻线处,调节天平平衡螺母使天平平衡。指针指向分度盘右侧,重心在右侧,应将平衡螺母向左调节;
(2)在称量小矿石质量过程中,不能调节天平平衡螺母;矿石的质量=砝码质量+游码示数,即矿石质量为57.4g;
(3)根据图丁所示,矿石的体积为:V=80mL﹣60mL=20mL=20cm3,根据密度公式ρ=,可知矿石密度为2.72×103kg/m3。测量矿石体积时,考虑棉线的体积,则所测体积大于矿石实际体积,根据密度公式ρ=,测量值偏小。
故答案为:(1)水平、平衡螺母、左;(2)在称量过程中调节天平平衡螺母、57.4;(3)2.72×103、偏小。
17.解:(1)剩余的烧杯和食用油的质量为:m=50g+10g+0.8g=60.8g,
量筒中食用油的质量为:m=87.8g﹣60.8g=27g;
食用油的密度为:ρ===0.9g/cm3=0.9×103kg/m3。
(2)由甲图可知,指针指向分度盘的右侧,说明右侧的质量大,没有调节天平平衡,使得称量的物体的质量会偏小,因为两次测得烧杯和食用油(烧杯和剩余食用油)的总质量都偏小,且偏小的程度相同,导致量筒中食用油的质量测量准确,体积不变,故测出的密度不变。
故答案为:(1)0.9×103;(2)偏小;不变。
18.解:(1)用天平和量筒测量密度的实验原理是:ρ=。
(2)烧杯中的樱桃酒不能全部倒入量筒,导致体积测量偏小,密度测量值偏大。
正确实验步骤:
B.向烧杯中倒入适量的樱桃酒,测出烧杯和樱桃酒的总质量m2;
C.将烧杯中的樱桃酒全部倒入量筒中,读出量筒中樱桃酒的体积V;
A.用已调平衡的天平测出烧杯的质量为m1。
实验步骤为:BCA。
(3)量筒中樱桃酒的质量:m=m2﹣m1,
樱桃酒的密度:ρ==。
(4)烧杯中水的质量:m=116g﹣46g=70g,
烧杯中水的体积:V水===70cm3,
樱桃酒的体积和水的体积相等,所以樱桃酒的体积:V酒=V水=70cm3,
烧杯和樱桃酒的质量:m'=100g+5g+4g=109g,
烧杯中樱桃酒的质量:m''=109g﹣46g=63g,
樱桃酒的密度:ρ===0.9g/cm3。
故答案为:(1)ρ=;(2)烧杯中樱桃酒不能全部倒入量筒;BCA;(3)ρ=;(4)②70;③109;
④0.9。
同步测试
一.选择题
1.我们在用天平和量筒测量某种液体密度时,以下操作步骤中,不必要的是( )
A.将烧杯中的部分液体倒入量筒中,测出倒入量筒中的液体的体积
B.取适量的液体倒入烧杯中,用天平测出烧杯和液体的总质量
C.用天平测出空烧杯的质量
D.用天平测出烧杯和剩余液体的总质量
2.为了测出石块的密度,某同学先用天平测石块的质量,所加砝码和游码在标尺上的位置如图甲所示,接着用量筒和水测矿石的体积,其过程如图乙所示。下列判断错误的是( )
A.石块的质量是47.2g
B.石块的体积是18cm3
C.石块的密度是2.6×103kg/m3
D.若先测石块的体积,最终测得石块的密度会偏大
3.用密度为2.7×103kg/m3的铝制成甲、乙、丙三个大小不同的正方体。要求它们的边长分别是0.1m、0.2m和0.3m,制成后让质量检查员称出它们的质量,分别是3kg、21.6kg和54kg,质量检查员指出,有两个不合格,其中一个掺入了杂质为次品,另一个混入了空气泡为废品,则这三个正方体( )
A.甲为废品,乙为合格品,丙为次品
B.甲为合格品,乙为废品,丙为次品
C.甲为次品,乙为合格品,丙为废品
D.甲为废品,乙为次品,丙为合格品
4.某同学用托盘天平和量筒测量一小石块的密度,图甲是调节天平时的情形,图乙和图丙分别是测量石块质量和体积时的情形,下列说法中正确的是( )
A.甲图中应将平衡螺母向左调,使横梁平衡
B.乙图中测石块质量时,天平的示数是17.4g
C.由丙图量筒的示数测得石块的体积是40cm3
D.利用图中信息,可计算出石块的密度是1.72×103kg/m3
5.以下为某同学测定煤油密度的一些实验步骤,这些步骤中可省去的步骤是( )
①用天平称出空矿泉水瓶的质量m0
②在矿泉水瓶里装满水,用天平称出它们的总质量m1
③用天平称出矿泉水瓶装满煤油后的总质量m2
④用量筒测出矿泉水瓶里所盛煤油的体积V
⑤计算煤油的密度
A.①
B.②或④
C.③
D.都不能省去
6.王梦与其他三位同学先后测量同一小石块的密度,下表中数据是他们的测量结果。
学生
王梦
赵满
李明
张扬
小石块的密度
2.45g/cm3
2.52g/cm3
2.56g/cm3
2.60g/cm3
经查密度表可知,石块的密度为2.50g/cm3.则下列说法正确的是( )
A.赵满的结果可以接受,因为他的数据与2.50g/cm3最接近
B.张扬的结果不可以接受,因为他的数据与2.50g/cm3偏差最大
C.如果实验操作正确,数据真实,上述结果均有效
D.四位同学的实验都失败了,因为他们的测量值都不是2.50g/cm3
7.小明用利用托盘天平和量筒测量盐水的密度。部分操作过程如图所示,下列说法不正确的是( )
A.量筒中液体的体积是40cm3
B.盐水的密度是1.165×103kg/m3
C.如果按照B、A、C的顺序会使测量结果偏小
D.按照A、C、B顺序操作如果盘中5g砝码因生锈质量变大则测得盐水密度偏大
8.小明和同学一起做测小石块密度的实验。下表记录的是小明与其他三位同学测出的小石块密度(注:经查密度表可知,石块的密度为2.50g/cm3)下列说法正确的是( )
学生
小明
小华
小李
小张
小石块的密度g/cm3
2.45
2.52
2.56
2.54
A.四位考生的实验都失败了,因为密度表中石块的密度为2.50g/cm3
B.只有小华的数据可以接受,因为她的数据最接近密度表中的数据
C.只有小张的数据不可以接受,因为他的数据偏差最大
D.只要实验操作正确,数据真实,上述数据均有效
9.在一次课外活动中,某同学拾到一块小矿石,查阅相关资料获知该矿石的密度为2.50g/cm3.四位同学分别设计实验方案各自测得矿石的密度为ρ甲=2.48g/cm3、ρ乙=2.51g/cm3、ρ丙=2.47g/cm3,ρ丁=2.56g/cm3,则下列分析中正确的是( )
A.四位同学的测量是错误的,因为该矿石的密度值为2.50g/cm3
B.只有乙同学的测量是正确的,因为他测得的数据最接近矿石密度的真实值
C.只有丁同学的测量是错误的,因为他测得的数据与矿石密度的真实值偏差最大
D.只要实验方案合理、操作正确,数据真实,四位同学测量的数据都是有效的
10.小亮利用细钢针、量筒和适量的水测量一个形状不规则的小蜡块的密度。小亮正确的测量过程如图甲、乙、丙所示,图中V0、V1、V2分别是量筒中水面所对应的示数。已知水的密度为ρ水,则下列四个选项中,小蜡块密度ρ蜡的表达式正确的是( )
A.
B.
C.
D.
二.填空题
11.小明用天平和量筒测量矿石的密度。先把天平放在
桌面上,调节好天平后,测出矿石的质量如图所示,矿石的质量为
g,接着他测出矿石的体积为20cm3,则矿石的密度为
kg/m3。
12.初二年级某班一位同学用调好的天平测量一体积为8cm3的小石块的质量,当天平重新平衡时,天平右盘中的砝码和游码位置如图所示,该小石块的密度为
;而另一位同学测得乙物体的质量是甲物体质量的3倍,若甲、乙两物体的体积比为4:3,则甲、乙两物体的密度比为
。
13.小明利用天平、烧杯和量筒测量某种液体的密度,他将烧杯中倒入部分液体并记录总质量m,再将其倒入量筒中测得体积V,多次实验后得到如图所示的图象,根据图象可得烧杯的质量是
g,液体的密度是
kg/m3,聪明的小明发现此种测量方法会导致测量值
(选填“偏大”、“偏小”或“不变”)。
14.小明想测量植物油的密度,他先用天平测出烧杯和植物油的总质量(如图所示)为
g.然后将烧杯中的植物油倒一些到量筒中,测出其体积为20mL,再测出烧杯和剩下的植物油的质量为17.4g,则该植物油的密度为
g/cm3。
15.实验:测量某种食用油的密度。
(1)把天平放在水平桌面上,将游码移至零刻度处,然后调节
,使天平横梁平衡。
(2)进行下列实验操作:
A.用天平测量烧杯和剩余食用油的总质量m1;
B.将待测食用油倒入烧杯中,用天平测出烧杯和食用油的总质量m2;
C.将烧杯中食用油的一部分倒入量筒,测出这部分食用油的体积V;
以上操作的正确顺序是:
。
(3)现已测出m1是110g,根据图中的示数,m2=
;V=
;算出这种食用油的密度是
。
三.实验探究题
16.小贾同学在学习了密度的测量之后,准备测量身边矿石的密度。
(1)小贾将天平放在
台面上,把游码移至标尺左端0刻线处,发现天平的指针偏向如图甲,他应将
向
调,使天平横梁平衡。
(2)调节完毕后,他使用天平测量这一小矿石的质量如图乙所示,其操作错误是:
。改正错误后,他测出了小矿石的质量如图丙为
g。
(3)在测量小矿石体积时,他首先应该将适量的水倒入量筒中,然后再将小矿石缓慢浸没在量筒中,如图丁测出小矿石的体积,根据以上测量的质量和体积算出小矿石的密度为
kg/m3;在测量小矿石体积时,如果考虑棉线的体积,则测量值
(选填“偏大”、“不变”或“偏小”)。
17.小刚在测量食用油密度的实验中,先将天平放在水平桌面上,移动游码至标尺左端“0”刻度线后指针位置如图甲所示,他随即在天平左盘中放入盛有食用油的烧杯,在右盘中加入砝码,并移动游码,使天平平衡,测得烧杯和食用油的总质量为87.8g。
(1)随后,他提起烧杯向空量筒中倒入30.0mL的食用油,再将烧杯放入天平左盘中,当右盘所加砝码和游码位置如图乙所示时,天平再次平衡,于是他计算得出食用油的密度为
kg/m3。
(2)在开始测量质量前,小刚没有调节天平平衡,这使他第一次测得的烧杯和食用油的总质量
(选填“偏大”“不变”或“偏小”),在(1)中测得的食用油密度
(选填“偏大”“不变”或“偏小”)。
18.某物理兴趣小组需要测量某樱桃酒的密度,他们利用天平和量筒进行了测量,实验过程如下:
A.用已调平衡的天平测出烧杯的质量为m1;
B.向烧杯中倒入适量的樱桃酒,测出烧杯和樱桃酒的总质量m2;
C.将烧杯中的樱桃酒全部倒入量筒中,读出量筒中樱桃酒的体积V。
(1)该小组测量樱桃酒密度的原理是:
;
(2)经讨论,该小组实验方案存在较大的误差,产生较大误差的原因是:
,改进措施时只要把实验顺序变一下即可,请你写出合理的顺序(填步骤前的字母序号):
;
(3)改进后的计算密度的公式是:(用步骤中测量量的符号表示)
;
(4)小华不小心将量筒打碎了,小明想出了一个新方案:
①将空烧杯放在天平上,测出其质量为46g;
②在烧杯中倒入适量的水,将水面的位置标记在烧杯壁上。将盛有水的烧杯放在天平上,测出其质量为116g,则烧杯中水的体积为
cm3;
③将水倒出擦干,在烧杯中倒入樱桃酒至标记处,将此烧杯放在天平上,天平平衡时,右盘中砝码质量和游码的位置如图所示,则烧杯和樱桃酒的总质量为
g;
④计算得出樱桃酒的密度为
g/cm3。
参考答案
一.选择题
1.解:测液体密度,若先测空烧杯的质量,再测烧杯和液体总质量,最后将液体倒入量筒来测体积,这种做法会因烧杯壁粘液体而使测出的体积偏小,导致算出的液体密度偏大。
为防止容器壁粘液体带来实验误差,应先测烧杯和液体总质量,再将液体倒入量筒测出体积,最后测出剩余液体和烧杯的质量,用密度公式ρ=算出液体的密度。所以本题中选项C用天平测出空烧杯的质量是不必要的。
故选:C。
2.解:
A、图甲中矿石的质量m=20g+20g+5g+1.8g=46.8g,故A错误;
B、图乙中水的体积为20cm3,水和矿石的总体积为38cm3,矿石的体积V=38cm3﹣20cm3=18cm3,故B正确;
C、矿石的密度ρ===2.6g/cm3=2.6×103kg/m3,故C正确;
D、若先测石块的体积,石块从量筒中取出会带着水,使的质量测量值偏大,则测量的密度值偏大,故D正确。
故选:A。
3.解:甲的体积:V甲=0.1m×0.1m×0.1m=0.001m3,则甲的密度:ρ甲===3×103kg/m3;
乙的体积:V乙=0.2m×0.2m×0.2m=0.008m3,则乙的密度:ρ乙===2.7×103kg/m3;
丙的体积:V丙=0.3m×0.3m×0.3m=0.027m3,则丙的密度:ρ丙===2×103kg/m3。
因为ρ乙=ρ铝,所以乙是合格品;因为ρ丙<ρ铝,所以丙是废品;因为ρ甲>ρ铝,所以甲是次品。
故选:C。
4.解:A、由图甲知,指针左偏,应将平衡螺母向右调使横梁平衡,故A错误;
B、由图乙知,标尺的分度值为0.2g,石块的质量m=10g+5g+2.2g=17.2g,故B错误,
C、由图丙知,水的体积为30mL,水和石块的总体积为40mL,
则石块的体积V=40mL﹣30mL=10mL=10cm3,故C错误;
D、石块的密度ρ===1.72g/cm3=1.72×103kg/m3,故D正确。
故选:D。
5.解:(1)为测出一定体积液体的质量,要根据矿泉水瓶的质量与煤油质量的和减去矿泉水瓶的质量,因此①不能省去;
(2)一定质量的煤油的体积可由量筒量出,或根据水的质量与密度求出其体积,所以可省去②或④,所以B正确;
(3)要根据矿泉水瓶的质量与煤油质量的和减去矿泉水瓶的质量而得出煤油的质量,因此③不能省去;
(4)由以上分析可得,D不正确。
故选:B。
6.解:在实验中,只要操作正确,数据便是真实的。
几个组数据的不同,是因为在测量过程中存在误差,所以如果实验操作正确,数据真实,上述结果均有效,故ABD错误,C正确。
故选:C。
7.解:
A、量筒的分度值为1cm3,量筒中盐水的体积为V=40cm3;故A正确;
B、在天平的标尺上,1g之间有5个小格,一个小格代表的质量是0.2g,即天平的分度值为0.2g;烧杯和盐水的总质量是m1=50g+20g+10g+2.4g=82.4g;
剩余盐水和烧杯的质量为m2=20g+10g+5g+0.8g=35.8g,
量筒中盐水的质量为m=m1﹣m2=82.4g﹣35.8g=46.6g,
盐水的密度为ρ==,=1.165g/cm3=1.165×103kg/m3;故B正确;
C、如果按照B、A、C的顺序,盐水质量准确,但是,由于一部分液体附着在烧杯壁上,倒入量筒中的盐水比实际偏小,由公式ρ=判断密度偏大,故C错误;
D、如果砝码生锈,则砝码的质量比实际值较大,所以当左盘放置1kg的物体时,右盘只需放置小于1kg的砝码即可,所以称得质量比实际质量偏小,则两次质量测量之差偏大,由公式ρ=得密度偏大,故D正确。
故选:C。
8.解:在实验中,只要操作正确,数据便是真实的。几个组数据的不同,是因为在测量过程中存在误差的原因。故ABC选项错误,D选项正确。
故选:D。
9.解:因为四位同学所测得都与真实值相差不大,只要实验方案合理、操作正确,数据真实,四位同学测量的数据都是有效的,故ABC错误,D正确。
故选:D。
10.解:
小蜡块漂浮在水面上,受到的重力等于排开水的重力,
由图甲和乙可知,小蜡块的质量等于它排开水的质量,
所以,m=m排水=(V1﹣V0)ρ水,
由甲和丙可知,小蜡块的体积为V=V2﹣V0,
所以小蜡块的密度:ρ==。
故选:B。
二.填空题
11.解:
天平使用时,应先杷天平放在水平桌面上;
由图知,天平标尺的分度值0.2g,矿石的质量:m=50g+2g=52g;
由题知,矿石的体积为20cm3,矿石的密度:ρ===2.6g/cm3=2.6×103kg/m3。
故答案为:水平;52;2.6×103。
12.解:
(1)由图知,称量标尺的分度值为0.2g,游码显示的示数为2.6g,物体的质量为:
m=10g+5g+2.6g=17.6g;
甲的密度为:
ρ甲===2.2g/cm3;
(2)由题知,m甲:m乙=1:3,V甲:V乙=4:3,
甲、乙两物体的密度:
ρ甲:ρ乙=:=×=×=1:4。
故答案为:2.2g/cm3;1:4。
13.解:由图象可知,当液体的体积由20cm3增加到80cm3时,液体的质量增加了m=100g﹣40g=60g;即60g的液体的体积为:V=80cm3﹣20cm3=60cm3;
则液体的密度为:ρ===1g/cm3=1×103kg/m3;
由图可知,当液体的体积为V'=20cm3时,总的质量为40g;
20cm3的液体的质量为:m'=ρV'=1g/cm3×20cm3=20g;
则烧杯的质量为:40g﹣20g=20g;
把烧杯中的液体全部倒入量筒中时,烧杯内的液体不可能全部倒入量筒中,烧杯内有液态的残留,会使得倒入量筒中液体的体积变小,根据ρ=可知,液体的密度偏大。
故答案为:20;1×103;偏大。
14.解:∵将砝码的质量加上游码所对应的刻度就是烧杯和植物油的总质量,
∴由图示可得烧杯和植物油的总质量为:20g+10g+3.4g=33.4g。
∵量筒内植物油的质量等于烧杯和植物油的总质量减去烧杯和剩余植物油的质量,
∴量筒内植物油的质量为:33.4g﹣17.4g=16g。
又∵测出量筒内植物油的体积为20ml,即20cm3。
∴根据密度公式ρ=得:ρ油===0.8g/cm3。
故答案为:33.4;0.8。
15.解:(1)把天平放在水平桌面上,将游码移至零刻度处,然后调节平衡螺母,使横梁平衡;
(2)测量液体密度的实验步骤为:先测出烧杯和食用油的总质量,再将一部分食用油倒入量筒读出体积,再测出烧杯和剩余食用油的总质量,
故操作的正确顺序是:BCA;
(3)图中烧杯和食用油的总质量m2=100g+50g+1.4g=151.4g,
量筒中食用油的质量m=m2﹣m1=151.4g﹣110g=41.4g,
量筒中食用油的体积V=46cm3,
食用油的密度ρ===0.9g/cm3。
故答案为:(1)平衡螺母;(2)BCA;(3)151.4g;46cm3;0.9g/cm3。
三.实验探究题
16.解:(1)天平在使用,应放在水平水平台面上;使用前调平衡,将游码用镊子拨动到标尺左端零刻线处,调节天平平衡螺母使天平平衡。指针指向分度盘右侧,重心在右侧,应将平衡螺母向左调节;
(2)在称量小矿石质量过程中,不能调节天平平衡螺母;矿石的质量=砝码质量+游码示数,即矿石质量为57.4g;
(3)根据图丁所示,矿石的体积为:V=80mL﹣60mL=20mL=20cm3,根据密度公式ρ=,可知矿石密度为2.72×103kg/m3。测量矿石体积时,考虑棉线的体积,则所测体积大于矿石实际体积,根据密度公式ρ=,测量值偏小。
故答案为:(1)水平、平衡螺母、左;(2)在称量过程中调节天平平衡螺母、57.4;(3)2.72×103、偏小。
17.解:(1)剩余的烧杯和食用油的质量为:m=50g+10g+0.8g=60.8g,
量筒中食用油的质量为:m=87.8g﹣60.8g=27g;
食用油的密度为:ρ===0.9g/cm3=0.9×103kg/m3。
(2)由甲图可知,指针指向分度盘的右侧,说明右侧的质量大,没有调节天平平衡,使得称量的物体的质量会偏小,因为两次测得烧杯和食用油(烧杯和剩余食用油)的总质量都偏小,且偏小的程度相同,导致量筒中食用油的质量测量准确,体积不变,故测出的密度不变。
故答案为:(1)0.9×103;(2)偏小;不变。
18.解:(1)用天平和量筒测量密度的实验原理是:ρ=。
(2)烧杯中的樱桃酒不能全部倒入量筒,导致体积测量偏小,密度测量值偏大。
正确实验步骤:
B.向烧杯中倒入适量的樱桃酒,测出烧杯和樱桃酒的总质量m2;
C.将烧杯中的樱桃酒全部倒入量筒中,读出量筒中樱桃酒的体积V;
A.用已调平衡的天平测出烧杯的质量为m1。
实验步骤为:BCA。
(3)量筒中樱桃酒的质量:m=m2﹣m1,
樱桃酒的密度:ρ==。
(4)烧杯中水的质量:m=116g﹣46g=70g,
烧杯中水的体积:V水===70cm3,
樱桃酒的体积和水的体积相等,所以樱桃酒的体积:V酒=V水=70cm3,
烧杯和樱桃酒的质量:m'=100g+5g+4g=109g,
烧杯中樱桃酒的质量:m''=109g﹣46g=63g,
樱桃酒的密度:ρ===0.9g/cm3。
故答案为:(1)ρ=;(2)烧杯中樱桃酒不能全部倒入量筒;BCA;(3)ρ=;(4)②70;③109;
④0.9。
同课章节目录
- 科学之旅
- 第一章 机械运动
- 第1节 长度和时间的测量
- 第2节 运动的描述
- 第3节 运动的快慢
- 第4节 测量平均速度
- 第二章 声现象
- 第1节 声音的产生和传播
- 第2节 声音的特性
- 第3节 声的利用
- 第4节 噪声的危害和控制
- 第三章 物态变化
- 第1节 温度
- 第2节 熔化和凝固
- 第3节 汽化和液化
- 第4节 升华和凝华
- 第四章 光现象
- 第1节 光的直线传播
- 第2节 光的反射
- 第3节 平面镜成像
- 第4节 光的折射
- 第5节 光的色散
- 第五章 透镜及其应用
- 第1节 透镜
- 第2节 生活中的透镜
- 第3节 凸透镜成像的规律
- 第4节 眼睛和眼镜
- 第5节 显微镜和望远镜
- 第六章 质量和密度
- 第1节 质量
- 第2节 密度
- 第3节 测量物质的密度
- 第4节 密度与社会生活
