苏科版数学八年级上册 6.1 函数 学案(无答案)
文档属性
| 名称 | 苏科版数学八年级上册 6.1 函数 学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 79.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览


文档简介
_____
6.1
函数(1)
【学习目标】
1.探索实际生活中的数量关系和变化规律,了解常量、变量的意义;
2.了解函数的概念,能举出函数的实例,会用函数表达式描述两个变量的关系;
【学习重点与难点】
重点:函数的概念,用函数表达式表示函数关系
难点:函数的概念
【学习过程】
一、目标导入
1.列车从无锡匀速开往上海,全程133km,G7201次列车9:33从无锡发车,10:29到达上海.在列车运行过程中,哪些量没有变化?哪些量不断有变化?
2.如图,用火柴棒按以下方式搭小鱼,搭1条小鱼用8根火柴棒,搭1条小鱼用14根火柴棒,每多搭一条小鱼就要增加_____根火柴棒,那么搭n条小鱼所用火柴棒的根数为S=_____________。
二、自主探究
探究一:
在某一变化过程中,常量是指________________________________;
变量是指_________________________________.
练习1:某水库总库容量为2.5×108m3,其水位高低与相应的蓄水量如下表所示:
水位/m
106
120
133
135
…
蓄水量/m3
2.30×107
7.09×107
1.18×108
1.25×108
…
说说该变化过程中,常量、变量分别有哪些?变量之间存在怎样的联系?
练习2:请你举一个存在变量和常量的变化过程,并说明变量间有怎样的联系?
探究二:
向平静的湖面投一石子,便会形成以落水点为圆心的一系列同心圆。
①
在这个变化过程中,有哪些变量?
②
若面积用S,半径用r表示,则S和r的关系是什么?π是常量还是变量?
③
若周长用C,半径用r表示,C与r的关系式是什么?
上述的每个变化过程中,都有___个变量,其中一个变量取值变化时,另一个变量________;一个变量确定时,另一个变量____________。
一般地,在一个变化过程中的两个变量x和y,如果_________________________________,那么我们称y是x的函数,其中x是自变量。
练习1:指出上述变化过程中的自变量和函数。
练习2:火车以90km/h的速度行驶,它行驶的路程S(千米)和时间t(小时)之间的函数关系式是
.其中常量是
,变量是
,
是
的函数.
三、小组交流与展示
四、巩固拓展
1.判断下列变量间y是否x的函数?为什么?
(1)y=3x+2
;
(2)y2=x
;
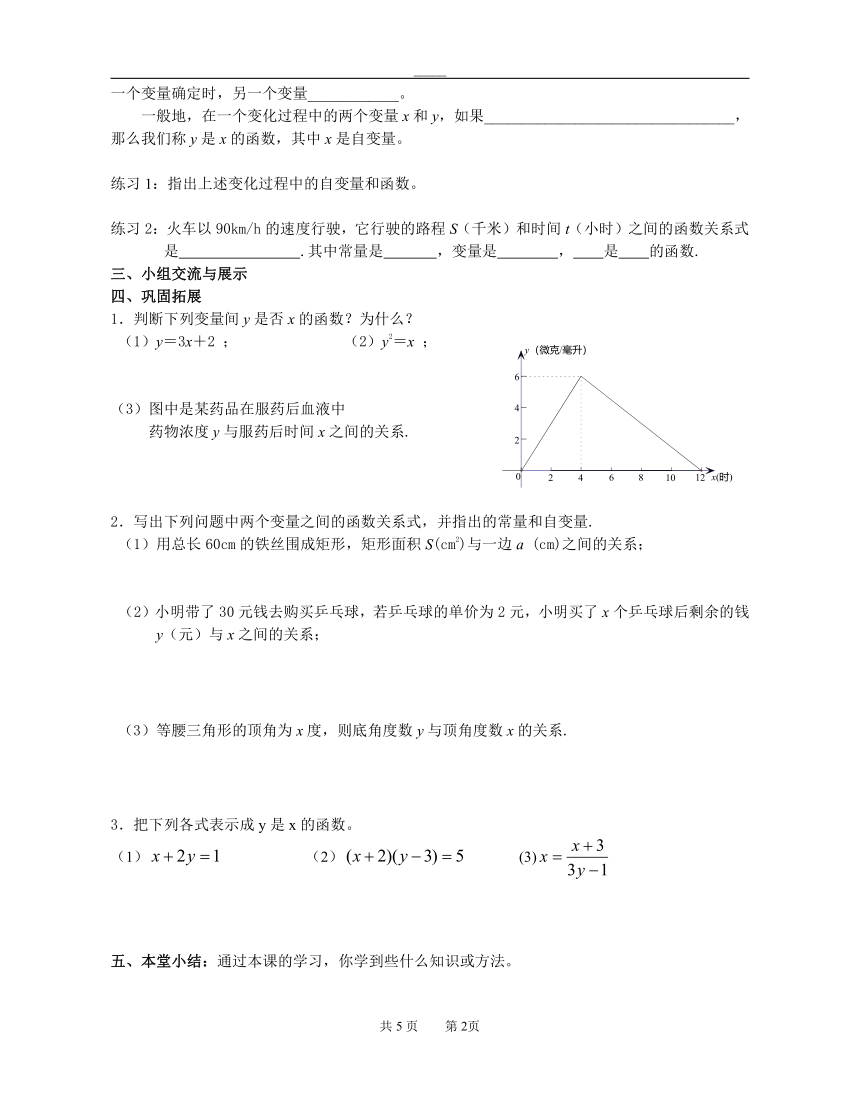
(3)图中是某药品在服药后血液中
药物浓度y与服药后时间x之间的关系.
2.写出下列问题中两个变量之间的函数关系式,并指出的常量和自变量.
(1)用总长60cm的铁丝围成矩形,矩形面积S(cm2)与一边a
(cm)之间的关系;
(2)小明带了30元钱去购买乒乓球,若乒乓球的单价为2元,小明买了x个乒乓球后剩余的钱y(元)与x之间的关系;
(3)等腰三角形的顶角为x度,则底角度数y与顶角度数x的关系.
3.把下列各式表示成y是x的函数。
(1)
(2)
(3)
五、本堂小结:通过本课的学习,你学到些什么知识或方法。
6.1
函数(1)---课后延伸
1.(1)设地面温度为18℃,如果每升高1km,气温就下降6℃,则气温t与高度h之间的函数关系式
,其中的常量是_______,变量是_______,______是_______的函数.
(2)若1吨民用自来水的价格是2.8元,则所交水费金额y(元)与自来水的数量x(吨)之间的关系式为______________,自变量是_________,
________是________的函数.
(3)一幢商住楼底层为店面房,底层高为4米,底层以上每层高3米,则楼高h与层数n之间的关系式为
h=
,
是
的函数。
(4)长方形的长为a,宽为b,则它的周长L=_____________,L是a、b的函数吗?
2.下列四个正方形都是由若干个棋子围成的图案,图案的每条边(包括两个端点)上都有n个棋子,每个图案的棋子总数为s,根据下图的规律用式子表示出s与n的关系,并说出其中的变量与常量.
3.用总长为60m的篱笆围成矩形的场地,求矩形面积S(m2)与一边长a(m)之间的关系式,并指出式中的常量和变量,哪个是自变量,哪个是函数?
4.已知x2+y=5,判断下列说法是否正确。
(1)y是x的函数;
(2)x是y的函数。
5.如图是某地冬季某一天的气温随时间变化的图象.看图回答:
(1)这天的6时、10时和14时的气温分别是
_________________________.
(2)这一天中,最高气温是_______________,
最低气温是_____________.
(3)这一天中,气温在逐渐升高的时段是__________,
气温在逐渐降低的时段是__________________.
(4)T是t的函数吗?
能否将T作为自变量,t是T的函数?为什么?
6.我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水.若拧不紧的水龙头每秒钟会滴下2滴水,每滴水约0.05毫升.小明同学在洗手时,没有把水龙头拧紧,当小明离开x小时后水龙头滴了y毫升水.
(1)写出y关于x的函数表达式。
(2)当小明离开5小时后,滴了多少毫升水?
6.1
函数(1)——归理拓展
1.下表是我市2008年统计的男学生各年龄组的平均身高。
年龄组(岁)
7
8
9
10
11
12
13
14
15
16
17
平均身高(cm)
115
118
122
127
130
136
148
155
158
165
172
(1)从上表可看出我市14岁的男学生的平均身高是
;
(2)我市男学生的平均身高从
岁开始迅速增加;
(3)上表反映了变量
和
之间的关系,其中
是自变量,
是因变量。
2.写出下列各个问题中的关系式,并指出其中的常量、变量和函数:
(1)圆周长C与半径r之间的关系;
关系式:
常量是
;变量是
;
是
的函数。
(2)某公司今年的年产量为100万件,计划以后每年增加2万件,则年产量y(万件)与年数(x)之间的关系;
关系式:
常量是
;变量是
;
是
的函数。
(3)矩形周长为30,面积y与一条边长x之间的关系;
关系式:
常量是
;变量是
;
是
的函数。
(4)汽车油箱中原有油100升,汽车每行驶50千米耗油10升,油箱剩余油量y(升)与汽车行驶路程x(千米)之间的关系。
关系式:
常量是
;变量是
;
是
的函数。
3.把下列各式表示成y是x的函数:
(1);
(2);
(3)
4.判断下列问题中的变量是否函数关系,简单说明理由。
(1)球的表面积S与球半径r的关系是,其中的S与r;
(2)设地面温度为18°C,如果每升高1km,气温将下降6°C,则气温t与高度h的关系;
(3)梯形的面积S与上底a、下底4、高h的关系;
5.(1)仿照已填好的数,填写如图所示的加法表,然后把
所有填有10的格子涂黑,看看你能发现什么?
(2)如果把这些涂黑的格子横向的加数用x表示,纵向的
加数用y表示,则y与x的函数关系式为
。
6.在某次实验中,测得两个变量m和n之间的4组对应数据如下表:
n
1
2
3
4
m
2.01
4.9
10.03
17.1
则m与n之间的关系最接近于下列各关系式中的(
)
A、
B、
C、
D、
7.如图,在矩形ABCD中,AB=4cm,AD=10cm,动点P由点A(起点)沿着折线ABCD向点D(终点)移动。设点P移动的路程为x(cm),△DAP的面积为S(cm2),试列出S与x之间的函数关系式。
共5页
第1页
6.1
函数(1)
【学习目标】
1.探索实际生活中的数量关系和变化规律,了解常量、变量的意义;
2.了解函数的概念,能举出函数的实例,会用函数表达式描述两个变量的关系;
【学习重点与难点】
重点:函数的概念,用函数表达式表示函数关系
难点:函数的概念
【学习过程】
一、目标导入
1.列车从无锡匀速开往上海,全程133km,G7201次列车9:33从无锡发车,10:29到达上海.在列车运行过程中,哪些量没有变化?哪些量不断有变化?
2.如图,用火柴棒按以下方式搭小鱼,搭1条小鱼用8根火柴棒,搭1条小鱼用14根火柴棒,每多搭一条小鱼就要增加_____根火柴棒,那么搭n条小鱼所用火柴棒的根数为S=_____________。
二、自主探究
探究一:
在某一变化过程中,常量是指________________________________;
变量是指_________________________________.
练习1:某水库总库容量为2.5×108m3,其水位高低与相应的蓄水量如下表所示:
水位/m
106
120
133
135
…
蓄水量/m3
2.30×107
7.09×107
1.18×108
1.25×108
…
说说该变化过程中,常量、变量分别有哪些?变量之间存在怎样的联系?
练习2:请你举一个存在变量和常量的变化过程,并说明变量间有怎样的联系?
探究二:
向平静的湖面投一石子,便会形成以落水点为圆心的一系列同心圆。
①
在这个变化过程中,有哪些变量?
②
若面积用S,半径用r表示,则S和r的关系是什么?π是常量还是变量?
③
若周长用C,半径用r表示,C与r的关系式是什么?
上述的每个变化过程中,都有___个变量,其中一个变量取值变化时,另一个变量________;一个变量确定时,另一个变量____________。
一般地,在一个变化过程中的两个变量x和y,如果_________________________________,那么我们称y是x的函数,其中x是自变量。
练习1:指出上述变化过程中的自变量和函数。
练习2:火车以90km/h的速度行驶,它行驶的路程S(千米)和时间t(小时)之间的函数关系式是
.其中常量是
,变量是
,
是
的函数.
三、小组交流与展示
四、巩固拓展
1.判断下列变量间y是否x的函数?为什么?
(1)y=3x+2
;
(2)y2=x
;
(3)图中是某药品在服药后血液中
药物浓度y与服药后时间x之间的关系.
2.写出下列问题中两个变量之间的函数关系式,并指出的常量和自变量.
(1)用总长60cm的铁丝围成矩形,矩形面积S(cm2)与一边a
(cm)之间的关系;
(2)小明带了30元钱去购买乒乓球,若乒乓球的单价为2元,小明买了x个乒乓球后剩余的钱y(元)与x之间的关系;
(3)等腰三角形的顶角为x度,则底角度数y与顶角度数x的关系.
3.把下列各式表示成y是x的函数。
(1)
(2)
(3)
五、本堂小结:通过本课的学习,你学到些什么知识或方法。
6.1
函数(1)---课后延伸
1.(1)设地面温度为18℃,如果每升高1km,气温就下降6℃,则气温t与高度h之间的函数关系式
,其中的常量是_______,变量是_______,______是_______的函数.
(2)若1吨民用自来水的价格是2.8元,则所交水费金额y(元)与自来水的数量x(吨)之间的关系式为______________,自变量是_________,
________是________的函数.
(3)一幢商住楼底层为店面房,底层高为4米,底层以上每层高3米,则楼高h与层数n之间的关系式为
h=
,
是
的函数。
(4)长方形的长为a,宽为b,则它的周长L=_____________,L是a、b的函数吗?
2.下列四个正方形都是由若干个棋子围成的图案,图案的每条边(包括两个端点)上都有n个棋子,每个图案的棋子总数为s,根据下图的规律用式子表示出s与n的关系,并说出其中的变量与常量.
3.用总长为60m的篱笆围成矩形的场地,求矩形面积S(m2)与一边长a(m)之间的关系式,并指出式中的常量和变量,哪个是自变量,哪个是函数?
4.已知x2+y=5,判断下列说法是否正确。
(1)y是x的函数;
(2)x是y的函数。
5.如图是某地冬季某一天的气温随时间变化的图象.看图回答:
(1)这天的6时、10时和14时的气温分别是
_________________________.
(2)这一天中,最高气温是_______________,
最低气温是_____________.
(3)这一天中,气温在逐渐升高的时段是__________,
气温在逐渐降低的时段是__________________.
(4)T是t的函数吗?
能否将T作为自变量,t是T的函数?为什么?
6.我国是一个严重缺水的国家,大家应倍加珍惜水资源,节约用水.若拧不紧的水龙头每秒钟会滴下2滴水,每滴水约0.05毫升.小明同学在洗手时,没有把水龙头拧紧,当小明离开x小时后水龙头滴了y毫升水.
(1)写出y关于x的函数表达式。
(2)当小明离开5小时后,滴了多少毫升水?
6.1
函数(1)——归理拓展
1.下表是我市2008年统计的男学生各年龄组的平均身高。
年龄组(岁)
7
8
9
10
11
12
13
14
15
16
17
平均身高(cm)
115
118
122
127
130
136
148
155
158
165
172
(1)从上表可看出我市14岁的男学生的平均身高是
;
(2)我市男学生的平均身高从
岁开始迅速增加;
(3)上表反映了变量
和
之间的关系,其中
是自变量,
是因变量。
2.写出下列各个问题中的关系式,并指出其中的常量、变量和函数:
(1)圆周长C与半径r之间的关系;
关系式:
常量是
;变量是
;
是
的函数。
(2)某公司今年的年产量为100万件,计划以后每年增加2万件,则年产量y(万件)与年数(x)之间的关系;
关系式:
常量是
;变量是
;
是
的函数。
(3)矩形周长为30,面积y与一条边长x之间的关系;
关系式:
常量是
;变量是
;
是
的函数。
(4)汽车油箱中原有油100升,汽车每行驶50千米耗油10升,油箱剩余油量y(升)与汽车行驶路程x(千米)之间的关系。
关系式:
常量是
;变量是
;
是
的函数。
3.把下列各式表示成y是x的函数:
(1);
(2);
(3)
4.判断下列问题中的变量是否函数关系,简单说明理由。
(1)球的表面积S与球半径r的关系是,其中的S与r;
(2)设地面温度为18°C,如果每升高1km,气温将下降6°C,则气温t与高度h的关系;
(3)梯形的面积S与上底a、下底4、高h的关系;
5.(1)仿照已填好的数,填写如图所示的加法表,然后把
所有填有10的格子涂黑,看看你能发现什么?
(2)如果把这些涂黑的格子横向的加数用x表示,纵向的
加数用y表示,则y与x的函数关系式为
。
6.在某次实验中,测得两个变量m和n之间的4组对应数据如下表:
n
1
2
3
4
m
2.01
4.9
10.03
17.1
则m与n之间的关系最接近于下列各关系式中的(
)
A、
B、
C、
D、
7.如图,在矩形ABCD中,AB=4cm,AD=10cm,动点P由点A(起点)沿着折线ABCD向点D(终点)移动。设点P移动的路程为x(cm),△DAP的面积为S(cm2),试列出S与x之间的函数关系式。
共5页
第1页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
