北师大版九年级下册课件 1.5 三角函数在生活中的应用 (1)(16张)
文档属性
| 名称 | 北师大版九年级下册课件 1.5 三角函数在生活中的应用 (1)(16张) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 10:04:12 | ||
图片预览




文档简介
三角函数在生活中的应用
—— 文峰塔有多高
姚安文峰塔位于云南姚安坝子南面山冈上,是姚安历史上保存至今比较完整的古建筑之一,分九层,六方体,全塔用砖支砌,由塔基、须弥座、塔身三部分组成,内空心有十七级栗木十字架。是云南省保存较为完整的明代密檐式砖塔,具有较高的历史,文化艺术和科学价值。
教学目标
1. 巩固解直角三角形的知识,并用三角函数解决生活中的一些问题。
2.能够把实际问题转化为数学问题,借助已知条件中的值进行三角函数的计算,培养学生数学应用意识和解决问题的能力。
一定要记住哦!
1.特殊角的三角函数值表
要能记住有多好
三角函数
锐角α
正弦sinα
余弦cosα
正切tanα
300
450
600
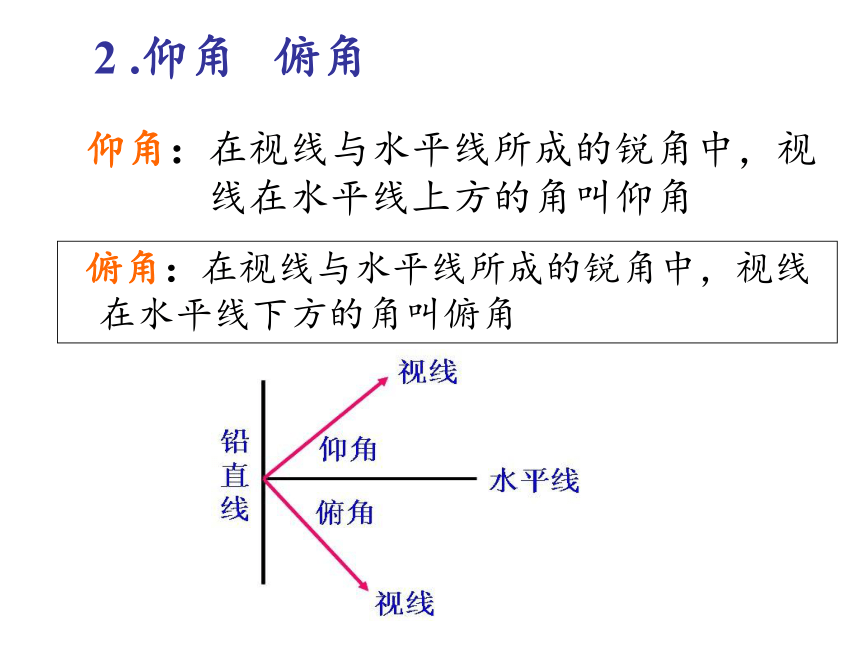
仰角:在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角
俯角:在视线与水平线所成的锐角中,视线 在水平线下方的角叫俯角
2 .仰角 俯角
B
A
30°
C
┌
x
B
45°
C
┌
x
A
C
A
B
┌
600
x
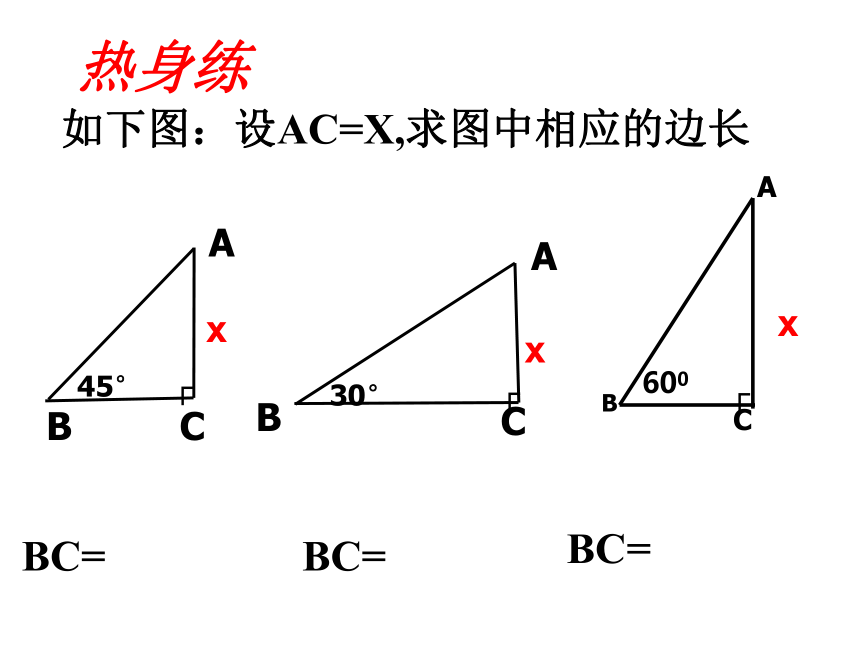
热身练
如下图:设AC=X,求图中相应的边长
BC=
BC=
BC=
D
B
45°
30°
C
┌
x
A
D
B
60°
30°
C
┌
x
A
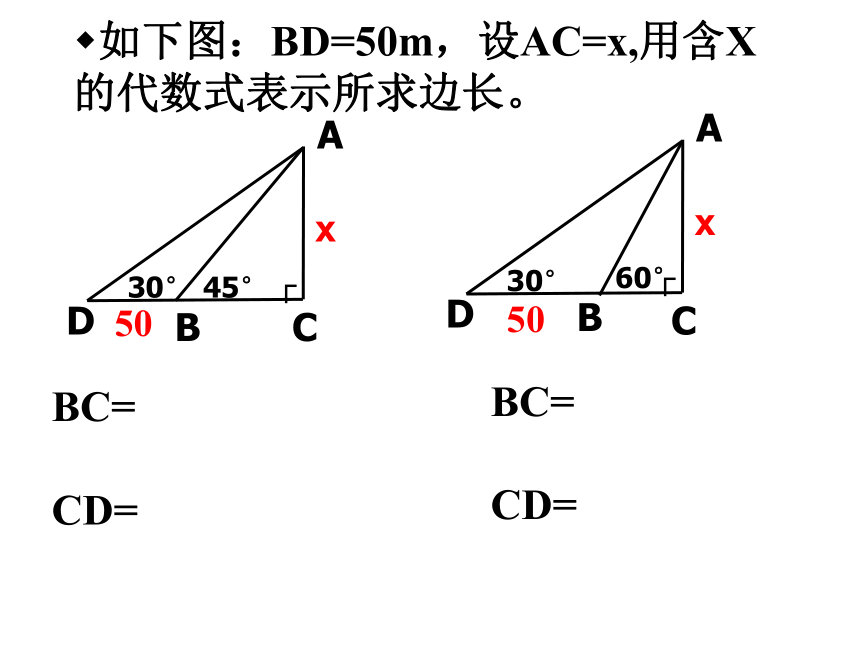
如下图:BD=50m,设AC=x,用含X的代数式表示所求边长。
BC=
CD=
BC=
CD=
50
50
文峰塔究竟有多高?
如图,小明想测量文峰塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进34m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到0.1m).
学以致用
要解决这问题,我们仍需将其数学化.
请与同伴交流你是怎么想的? 准备怎么去做?
现在你能完成这个任务吗?
?
这样解答
D
A
B
C
┌
50m
300
600
答:该塔约有43m高.
解:如图,根据题意知,CD⊥AC∠A=300,∠DBC=600,AB=50m.设CD=x,∠ADC=600,∠BDC=300,
在Rt△ACD中和在Rt△BCD中
这道题你能有更简单的解法吗?
1.在一个阳光明媚,微风习习的周末,小明和小强一起到梅葛广场放风筝,放了一会儿,两人争了起来:
小明说:“我的风筝飞得比你的高”.
小强说:“我的风筝引线比你的长,我的风筝飞得更高”.
谁的风筝飞得更高呢?于是他们将两个风筝引线的一端都固定在地面上的C处(如图).现已知小明的风筝引线(线段AC)长30米,小强的风筝引线(线段BC)长36米,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.请通过计算说明谁的风筝飞得更高?(结果精确到0.1米)
拓展与 应用
(参考数据: ≈1.414,
≈1.732)
2. 如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
解:如图,过B点作BE⊥CD于点E,
由题意得,四边形ABEC是矩形,
∴BE=AC=22,CE=AB=1.5
在Rt△BED中
∵∠DBE=32°
tan∠DBE= ,
∴DE=BE·tan32°≈22×0.62=13.64,
∴CD=DE+EC=13.64+1.5=15.14≈15.1(米).
答:旗杆CD的高度约为15.1米.
解:如图,过B点作BE⊥CD于点E,
由题意得,四边形ABEC是矩形,
∴BE=AC=22,CE=AB=1.5
在Rt△BED中
∵∠DBE=32°
tan∠DBE= ,
∴DE=BE·tan32°≈22×0.62=13.64,
∴CD=DE+EC=13.64+1.5=15.14≈15.1(米).
答:旗杆CD的高度约为15.1米.
校庆前摄制组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
自我挑战
解:如解图,作AD⊥BC,BH⊥水平线,由题意得:∠ACH=75°,∠BCH=30°,AB∥CH,
∴∠ABC=30°,∠ACB=45°
∵AB=4×8=32 米
∴AD=CD=AB·sin30°=16 米,
BD=AB·cos30°=16 米,
∴BC=CD+BD=(16+16 )米,
则BH=BC·sin30°=(8+8 )米.
故这架无人飞机的飞行高度是(8+8 )米.
课堂小结
1.将实际问题转化为数学问题;
(画出平面图形,转化为解直角三角形的问题)
2.根据条件的特点,适当选用锐角三角函数等
去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
—— 文峰塔有多高
姚安文峰塔位于云南姚安坝子南面山冈上,是姚安历史上保存至今比较完整的古建筑之一,分九层,六方体,全塔用砖支砌,由塔基、须弥座、塔身三部分组成,内空心有十七级栗木十字架。是云南省保存较为完整的明代密檐式砖塔,具有较高的历史,文化艺术和科学价值。
教学目标
1. 巩固解直角三角形的知识,并用三角函数解决生活中的一些问题。
2.能够把实际问题转化为数学问题,借助已知条件中的值进行三角函数的计算,培养学生数学应用意识和解决问题的能力。
一定要记住哦!
1.特殊角的三角函数值表
要能记住有多好
三角函数
锐角α
正弦sinα
余弦cosα
正切tanα
300
450
600
仰角:在视线与水平线所成的锐角中,视线在水平线上方的角叫仰角
俯角:在视线与水平线所成的锐角中,视线 在水平线下方的角叫俯角
2 .仰角 俯角
B
A
30°
C
┌
x
B
45°
C
┌
x
A
C
A
B
┌
600
x
热身练
如下图:设AC=X,求图中相应的边长
BC=
BC=
BC=
D
B
45°
30°
C
┌
x
A
D
B
60°
30°
C
┌
x
A
如下图:BD=50m,设AC=x,用含X的代数式表示所求边长。
BC=
CD=
BC=
CD=
50
50
文峰塔究竟有多高?
如图,小明想测量文峰塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进34m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到0.1m).
学以致用
要解决这问题,我们仍需将其数学化.
请与同伴交流你是怎么想的? 准备怎么去做?
现在你能完成这个任务吗?
?
这样解答
D
A
B
C
┌
50m
300
600
答:该塔约有43m高.
解:如图,根据题意知,CD⊥AC∠A=300,∠DBC=600,AB=50m.设CD=x,∠ADC=600,∠BDC=300,
在Rt△ACD中和在Rt△BCD中
这道题你能有更简单的解法吗?
1.在一个阳光明媚,微风习习的周末,小明和小强一起到梅葛广场放风筝,放了一会儿,两人争了起来:
小明说:“我的风筝飞得比你的高”.
小强说:“我的风筝引线比你的长,我的风筝飞得更高”.
谁的风筝飞得更高呢?于是他们将两个风筝引线的一端都固定在地面上的C处(如图).现已知小明的风筝引线(线段AC)长30米,小强的风筝引线(线段BC)长36米,在C处测得风筝A的仰角为60°,风筝B的仰角为45°.请通过计算说明谁的风筝飞得更高?(结果精确到0.1米)
拓展与 应用
(参考数据: ≈1.414,
≈1.732)
2. 如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
解:如图,过B点作BE⊥CD于点E,
由题意得,四边形ABEC是矩形,
∴BE=AC=22,CE=AB=1.5
在Rt△BED中
∵∠DBE=32°
tan∠DBE= ,
∴DE=BE·tan32°≈22×0.62=13.64,
∴CD=DE+EC=13.64+1.5=15.14≈15.1(米).
答:旗杆CD的高度约为15.1米.
解:如图,过B点作BE⊥CD于点E,
由题意得,四边形ABEC是矩形,
∴BE=AC=22,CE=AB=1.5
在Rt△BED中
∵∠DBE=32°
tan∠DBE= ,
∴DE=BE·tan32°≈22×0.62=13.64,
∴CD=DE+EC=13.64+1.5=15.14≈15.1(米).
答:旗杆CD的高度约为15.1米.
校庆前摄制组借助无人飞机航拍校园.如图,无人飞机从A处水平飞行至B处需8秒,在地面C处同一方向上分别测得A处的仰角为75°,B处的仰角为30°.已知无人飞机的飞行速度为4米/秒,求这架无人飞机的飞行高度.(结果保留根号)
自我挑战
解:如解图,作AD⊥BC,BH⊥水平线,由题意得:∠ACH=75°,∠BCH=30°,AB∥CH,
∴∠ABC=30°,∠ACB=45°
∵AB=4×8=32 米
∴AD=CD=AB·sin30°=16 米,
BD=AB·cos30°=16 米,
∴BC=CD+BD=(16+16 )米,
则BH=BC·sin30°=(8+8 )米.
故这架无人飞机的飞行高度是(8+8 )米.
课堂小结
1.将实际问题转化为数学问题;
(画出平面图形,转化为解直角三角形的问题)
2.根据条件的特点,适当选用锐角三角函数等
去解直角三角形;
3.得到数学问题的答案;
4.得到实际问题的答案.
