北师大版七年级上册数学课件:5.4 应用一元一次方程(15张)
文档属性
| 名称 | 北师大版七年级上册数学课件:5.4 应用一元一次方程(15张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 959.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览






文档简介
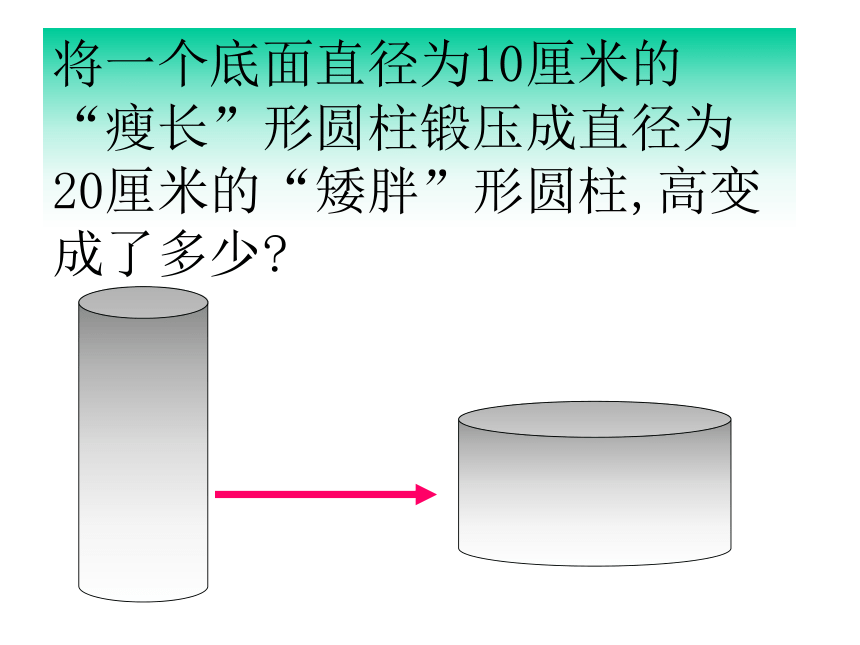
将一个底面直径为10厘米的“瘦长”形圆柱锻压成直径为20厘米的“矮胖”形圆柱,高变成了多少?
等量关系:锻压前的体积=锻压后的体积
设锻压后圆柱的高为x厘米,填写下表:
锻压前
锻压后
底面半径(厘米)
高(厘米)
体积(立方厘米)
根据等量关系,列出方程:
解得x=
因此,高变成了 厘米.
5 2∏×36=102∏x
9
9
5
10
36
x
5 2∏×36
102∏x
等积类
利息类
商品利润
工程类
行程类
比例类
浓度类
例题
等积类应用题:
变形前的体积(容积)=变形后的体积(容积)
利息类应用题:
本金× 利率=利息
本金+利息=本息和
商品利润率问题:
商品利润率=
商品利润=商品售价-商品进价
工程类应用题:
工程类应用题中的工作量并不是一个具体的数量,因而常常把工作量看作整体1
工作效率× 工作时间=工作量
行程类应用题:
路程=速度× 时间
相遇问题(相向而行):甲的路程+乙的路程=总路程
追及问题(同向而行):追者的路程=前者的路程+两地距离
顺水(风)或逆水(风)问题:
顺水(风)速度=静水(无风)速度+水(风)速
逆水(风)速度=静水(无风)速度-水(风)速
比例类应用题:
若甲、乙的比为2:3,可设甲为2x,乙为3x;
浓度类应用题:
浓度=
例、用一根长为10米的铁丝围成一个长方形。
(1)使得长方形的长比宽多1.4米,此时长方形的长与宽各为多少米?
(2)使得长方形的长比宽多0.8米,此时长方形的长与宽各为多少米?
这个长方形与(1)中的长方形相比,面积有什么变化?
(3)使得长方形的长与宽相等,即围成一个正方形,此时正方形的边长是多少?这个正方形与(2)中的长方形相比又有什么变化?
分析:无论长与宽如何变化,它们的周长如终是10米.
解: (1)设长方形的宽为x米,那么长为(x+1.4)米,根据题意,有
2(x+x+1.4)=10
解得x=1.8
因此,长方形的长为1.8+1.4=3.2米,宽为1.8米.围成长方形的面积是
3.2× 1.8=5.76米2
(2)设长方形的宽为x米,那么长为( x+0.8)米,根据题意,有
2(x+x+0.8)=10
解得x=2.1
因此,长方形的长为2.1+0.8=2.9米,宽为2.1米.围成长方形的面积是2.1× 2.9=6.09米2..比(1)中长方形的面积增加了6.09-5.76=0.33米2
(3)设正方形的边长为x米,根据题意,有
2(x+x)=10
解得x=2.5
因此正方形的边长为2.5米.围成正方形的面积是2.5× 2.5=6.25米2.比(2)中的长方形的面积增加了6.25-6.09=0.16米2
布置作业:
课本习题中数学理解第1题.
等量关系:锻压前的体积=锻压后的体积
设锻压后圆柱的高为x厘米,填写下表:
锻压前
锻压后
底面半径(厘米)
高(厘米)
体积(立方厘米)
根据等量关系,列出方程:
解得x=
因此,高变成了 厘米.
5 2∏×36=102∏x
9
9
5
10
36
x
5 2∏×36
102∏x
等积类
利息类
商品利润
工程类
行程类
比例类
浓度类
例题
等积类应用题:
变形前的体积(容积)=变形后的体积(容积)
利息类应用题:
本金× 利率=利息
本金+利息=本息和
商品利润率问题:
商品利润率=
商品利润=商品售价-商品进价
工程类应用题:
工程类应用题中的工作量并不是一个具体的数量,因而常常把工作量看作整体1
工作效率× 工作时间=工作量
行程类应用题:
路程=速度× 时间
相遇问题(相向而行):甲的路程+乙的路程=总路程
追及问题(同向而行):追者的路程=前者的路程+两地距离
顺水(风)或逆水(风)问题:
顺水(风)速度=静水(无风)速度+水(风)速
逆水(风)速度=静水(无风)速度-水(风)速
比例类应用题:
若甲、乙的比为2:3,可设甲为2x,乙为3x;
浓度类应用题:
浓度=
例、用一根长为10米的铁丝围成一个长方形。
(1)使得长方形的长比宽多1.4米,此时长方形的长与宽各为多少米?
(2)使得长方形的长比宽多0.8米,此时长方形的长与宽各为多少米?
这个长方形与(1)中的长方形相比,面积有什么变化?
(3)使得长方形的长与宽相等,即围成一个正方形,此时正方形的边长是多少?这个正方形与(2)中的长方形相比又有什么变化?
分析:无论长与宽如何变化,它们的周长如终是10米.
解: (1)设长方形的宽为x米,那么长为(x+1.4)米,根据题意,有
2(x+x+1.4)=10
解得x=1.8
因此,长方形的长为1.8+1.4=3.2米,宽为1.8米.围成长方形的面积是
3.2× 1.8=5.76米2
(2)设长方形的宽为x米,那么长为( x+0.8)米,根据题意,有
2(x+x+0.8)=10
解得x=2.1
因此,长方形的长为2.1+0.8=2.9米,宽为2.1米.围成长方形的面积是2.1× 2.9=6.09米2..比(1)中长方形的面积增加了6.09-5.76=0.33米2
(3)设正方形的边长为x米,根据题意,有
2(x+x)=10
解得x=2.5
因此正方形的边长为2.5米.围成正方形的面积是2.5× 2.5=6.25米2.比(2)中的长方形的面积增加了6.25-6.09=0.16米2
布置作业:
课本习题中数学理解第1题.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
