北师大版九年级下册数学第三章圆单元复习题(word版无答案)
文档属性
| 名称 | 北师大版九年级下册数学第三章圆单元复习题(word版无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 169.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览

文档简介
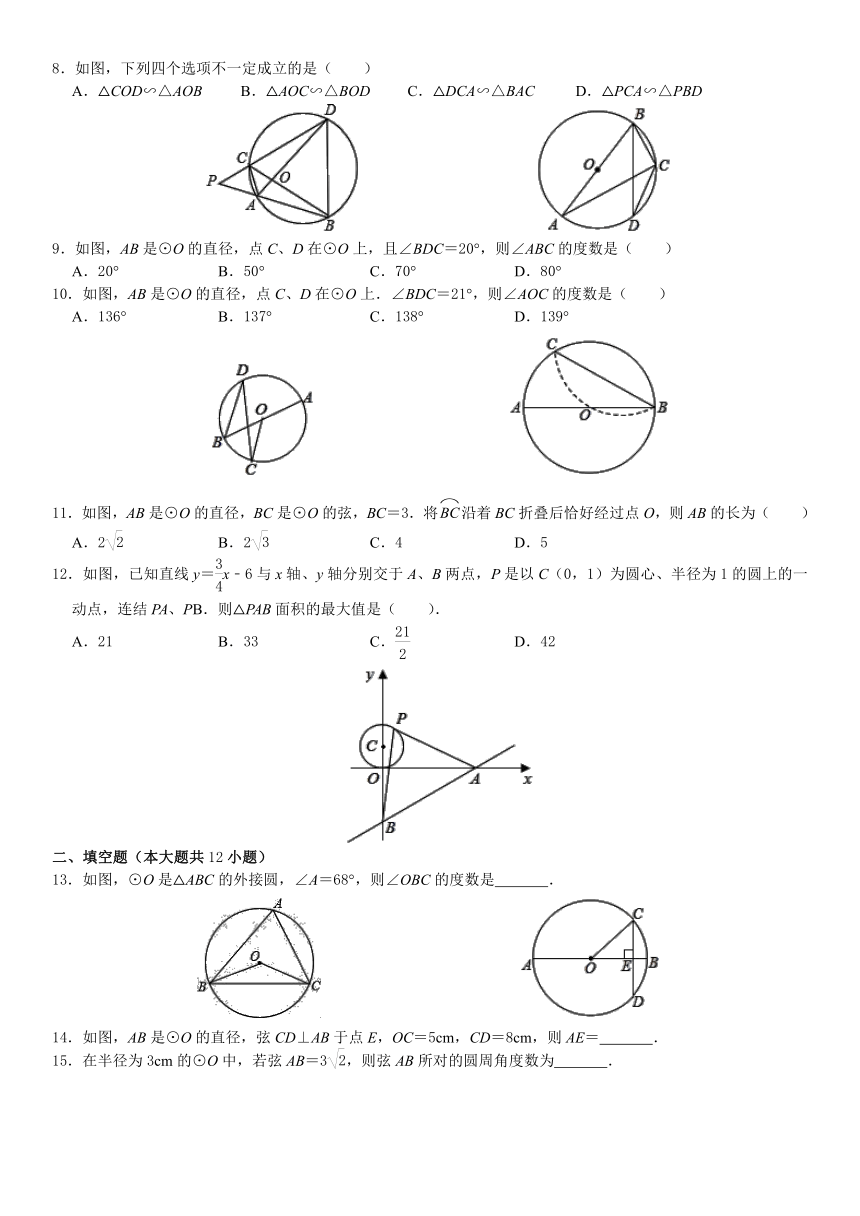
北师大版九年级下数学第三章圆单元复习题
一、选择题(本大题共12小题)
1.如图,AB是⊙O的直径,点C在⊙O上,∠ABC=30°,AC=4,则⊙O的半径为( )
A.4
B.8
C.
D.
2.如图,AB是⊙O的直径,点C、D在⊙O上.若∠BOD=130°,则∠ACD的度数为( )
A.50°
B.30°
C.25°
D.20°
3.如图,在平面直角坐标系xOy中,点A为(0,3),点B为(2,1),点C为(2,﹣3).则经画图操作可知:△ABC的外心坐标应是( )
A.(0,0)
B.(1,0)
C.(﹣2,﹣1)
D.(2,0)
4.如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD等于
A.
B.
C.
D.
5.如图,⊙O的直径AB经过CD的中点H,cos∠CDB=,BD=5,则OH的长度为( )
A.
B.
C.
D.
6.如图,已知AB和CD分别是半圆O的直径和弦,AD和BC相交于点E,若∠AEC=α,则S△CDE∶S△ABE等于(
)A.sin2α
B.cos2α
C.tan2α
D.与α无关
7.⊙O的半径为1,AB是⊙O
的一条弦,且AB=,则弦AB所对圆周角的度数为(
)
A.30°
B.60°
C.30°或150°
D.60°或120°
8.如图,下列四个选项不一定成立的是( )
A.△COD∽△AOB
B.△AOC∽△BOD
C.△DCA∽△BAC
D.△PCA∽△PBD
9.如图,AB是⊙O的直径,点C、D在⊙O上,且∠BDC=20°,则∠ABC的度数是( )
A.20°
B.50°
C.70°
D.80°
10.如图,AB是⊙O的直径,点C、D在⊙O上.∠BDC=21°,则∠AOC的度数是( )
A.136°
B.137°
C.138°
D.139°
11.如图,AB是⊙O的直径,BC是⊙O的弦,BC=3.将沿着BC折叠后恰好经过点O,则AB的长为( )
A.2
B.2
C.4
D.5
12.如图,已知直线y=x﹣6与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心、半径为1的圆上的一动点,连结PA、PB.则△PAB面积的最大值是( ).
A.21
B.33
C.
D.42
二、填空题(本大题共12小题)
13.如图,⊙O是△ABC的外接圆,∠A=68°,则∠OBC的度数是
.
14.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=
.
15.在半径为3cm的⊙O中,若弦AB=3,则弦AB所对的圆周角度数为
.
16.如图,四边形ABCD内接于⊙O,∠C=130°,则∠BOD的度数是__________.
17.如图,CB是⊙O的直径,P是CB延长线上一点,PB=2,PA切⊙O于A点,PA=4,则cosP=__________;
18.如图,⊙O的半径为6cm,直线AB是⊙O的切线,切点为点B,弦BC∥AO,若∠A=30°,则劣弧的长为_________cm.
19.如图,AB为⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠C=23°,则∠EOB的度数为
.
20.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为
.(结果保留π)
21.如图,AD是⊙O的直径,若∠B=40°,则∠DAC的度数为
.
22.如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,2),(2,0),(4,0),⊙M是△ABC的外接圆,则圆心M的坐标为
,⊙M的半径为
.
23.如图,四边形ABCD是菱形,∠B=60°,AB=1,扇形AEF的半径为1,圆心角为60°,则图中阴影部分的面积是 .
24.手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1.若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20= _____ .
三、解答题(本大题共5小题)
25.如图,AB是⊙O的直径,点D在AB的延长线上,AC平分∠DAE交⊙O于点C,且AE⊥DC的延长线,垂足为点E.
(1)求证:直线CD是⊙O的切线;
(2)若AB=6,BD=2,求CE的长.
26.如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C.
(1)若∠ADE=25°,求∠C的度数;
(2)若AC=4,CE=2,求⊙O半径的长.
27.如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
28.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由.
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧DE所围成的阴影部分的面积.(结果保留根号和)
29.如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),B(﹣4,0).
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C,求△BMC面积的最大值;
(3)在(2)中△BMC面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
一、选择题(本大题共12小题)
1.如图,AB是⊙O的直径,点C在⊙O上,∠ABC=30°,AC=4,则⊙O的半径为( )
A.4
B.8
C.
D.
2.如图,AB是⊙O的直径,点C、D在⊙O上.若∠BOD=130°,则∠ACD的度数为( )
A.50°
B.30°
C.25°
D.20°
3.如图,在平面直角坐标系xOy中,点A为(0,3),点B为(2,1),点C为(2,﹣3).则经画图操作可知:△ABC的外心坐标应是( )
A.(0,0)
B.(1,0)
C.(﹣2,﹣1)
D.(2,0)
4.如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD等于
A.
B.
C.
D.
5.如图,⊙O的直径AB经过CD的中点H,cos∠CDB=,BD=5,则OH的长度为( )
A.
B.
C.
D.
6.如图,已知AB和CD分别是半圆O的直径和弦,AD和BC相交于点E,若∠AEC=α,则S△CDE∶S△ABE等于(
)A.sin2α
B.cos2α
C.tan2α
D.与α无关
7.⊙O的半径为1,AB是⊙O
的一条弦,且AB=,则弦AB所对圆周角的度数为(
)
A.30°
B.60°
C.30°或150°
D.60°或120°
8.如图,下列四个选项不一定成立的是( )
A.△COD∽△AOB
B.△AOC∽△BOD
C.△DCA∽△BAC
D.△PCA∽△PBD
9.如图,AB是⊙O的直径,点C、D在⊙O上,且∠BDC=20°,则∠ABC的度数是( )
A.20°
B.50°
C.70°
D.80°
10.如图,AB是⊙O的直径,点C、D在⊙O上.∠BDC=21°,则∠AOC的度数是( )
A.136°
B.137°
C.138°
D.139°
11.如图,AB是⊙O的直径,BC是⊙O的弦,BC=3.将沿着BC折叠后恰好经过点O,则AB的长为( )
A.2
B.2
C.4
D.5
12.如图,已知直线y=x﹣6与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心、半径为1的圆上的一动点,连结PA、PB.则△PAB面积的最大值是( ).
A.21
B.33
C.
D.42
二、填空题(本大题共12小题)
13.如图,⊙O是△ABC的外接圆,∠A=68°,则∠OBC的度数是
.
14.如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=
.
15.在半径为3cm的⊙O中,若弦AB=3,则弦AB所对的圆周角度数为
.
16.如图,四边形ABCD内接于⊙O,∠C=130°,则∠BOD的度数是__________.
17.如图,CB是⊙O的直径,P是CB延长线上一点,PB=2,PA切⊙O于A点,PA=4,则cosP=__________;
18.如图,⊙O的半径为6cm,直线AB是⊙O的切线,切点为点B,弦BC∥AO,若∠A=30°,则劣弧的长为_________cm.
19.如图,AB为⊙O的直径,C是BA延长线上一点,点D在⊙O上,且CD=OA,CD的延长线交⊙O于点E,若∠C=23°,则∠EOB的度数为
.
20.如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,AB长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则贴纸的面积为
.(结果保留π)
21.如图,AD是⊙O的直径,若∠B=40°,则∠DAC的度数为
.
22.如图,在平面直角坐标系xOy中,点A,B,C的坐标分别是(0,2),(2,0),(4,0),⊙M是△ABC的外接圆,则圆心M的坐标为
,⊙M的半径为
.
23.如图,四边形ABCD是菱形,∠B=60°,AB=1,扇形AEF的半径为1,圆心角为60°,则图中阴影部分的面积是 .
24.手机上常见的wifi标志如图所示,它由若干条圆心相同的圆弧组成,其圆心角为90°,最小的扇形半径为1.若每两个相邻圆弧的半径之差为1,由里往外的阴影部分的面积依次记为S1、S2、S3…,则S1+S2+S3+…+S20= _____ .
三、解答题(本大题共5小题)
25.如图,AB是⊙O的直径,点D在AB的延长线上,AC平分∠DAE交⊙O于点C,且AE⊥DC的延长线,垂足为点E.
(1)求证:直线CD是⊙O的切线;
(2)若AB=6,BD=2,求CE的长.
26.如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点C.
(1)若∠ADE=25°,求∠C的度数;
(2)若AC=4,CE=2,求⊙O半径的长.
27.如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.
28.如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由.
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD,BE与劣弧DE所围成的阴影部分的面积.(结果保留根号和)
29.如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),B(﹣4,0).
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C,求△BMC面积的最大值;
(3)在(2)中△BMC面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
