一元二次方程根的判别式
图片预览






文档简介
(共18张PPT)
第17章 一元二次方程根的判别式
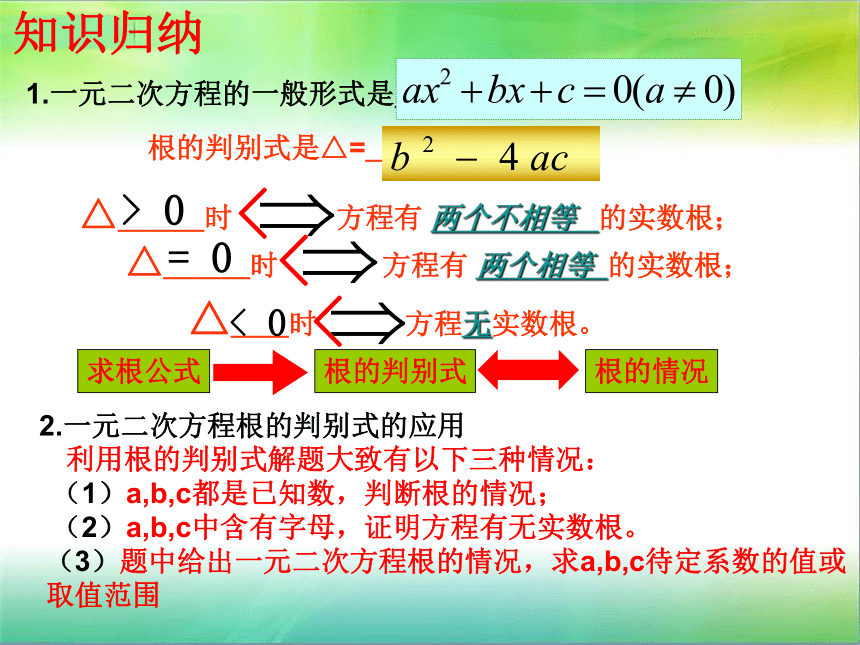
1.一元二次方程的一般形式是_________
根的判别式是△=________
△___时 方程有 两个不相等 的实数根;
△___时 方程有 两个相等 的实数根;
△__时 方程无实数根。
<
<
> 0
<
= 0
< 0
知识归纳
求根公式
根的判别式
根的情况
2.一元二次方程根的判别式的应用
利用根的判别式解题大致有以下三种情况:
(1)a,b,c都是已知数,判断根的情况;
(2)a,b,c中含有字母,证明方程有无实数根。
(3)题中给出一元二次方程根的情况,求a,b,c待定系数的值或取值范围
1.不解方程,判断下列方程的根的情况:
(1)
(2)
(3)
所以原方程有两个不相等的实数根。
解:
解:
解:
所以原方程无实数根。
所以原方程有两个相等的实数根。
△=
△=
△=
这里a=3,b=10,c=3
这里 a=16,b=-8,c=1
这里 a=2,b=-3,c=2
应用举例
2.关于x的方程 一定有实数根吗?为什么?
解:原方程变形为:
△=
=
=
∴
原方程一定有实数根。
点评:若要使一元二次方程有实数根,则需这方程的根的判别式大于或等于0,即Δ≥0( )。
3. 当m取何值时,关于x的方程
(1)有两个不相等的实数根?
(2)有两个相等的实数根?
(3)无实数根?
解:△=
(1)当-4m+8>0时,
即m<2时,方程有两个不相等的实数根
(2)当-4m+8=0时,
即m=2时,方程有两个相等的实数根
(3)当-4m+8<0时,
即m>2时,方程无实数根
1.不解方程,判断下列关于x的方程的根的情况:
(1)
(2)
(3)
(4)
解:
原方程变形为:
解:
解:
原方程变形为:
△=
<0
△=
=0
所以原方程无实数根
所以原方程有两个相等的实数根
△=
=
≥0
解:
△=
所以原方程有两个实数根
当c=0时,△=0,方程有两个相等的实数根,
当a与c异号时,ac<0,则-4ac>0,即△>0,方程有两个不相等的实数根
当a与c同号时,ac>0,则-4ac<0,即△<0,方程没有实数根
=-4ac
试一试,你一定可以!
2.已知关于x的方程
k取何值时,此方程
(1)有两个实数根;(2)有实数根
解:
(1)因为方程有两个实数根,所以
△≥0
且 k+1≠0,
即:
{
k+1≠0
解得:
且 k≠-1
且 k≠-1
当 时,
方程有两个实数根.
(2) 当方程是一元一次方程时,即当k+1=0,k=-1时,方程为:
方程有一个实数根。
-2x+3=0,
当方程是关于x的一元二次方程时,k应满足
{
k+1≠0
且 k≠-1
解得:
综合 得:当 时,关于x的方程有实数根。
3 已知关于x的方程
有两个相等的实数根,求k的值及这时方程的根
解:
由题意得:
Δ=0 时,方程有两个相等的实数根。
解这个方程得: k1=2, k2=10
整理得:
原方程整理为:
即:
(1)当k=2时,原方程为:
解这个方程得 : x1=x2=
解这个方程得 : x3=x4=
(2)当k=10时,原方程为:
点评:在利用根的判别式解题时,一定要先把方程化为一般形式,确定了a,b,c,并正确算出
的值,然后根据判别式的取值与一元二次方程根的关系列出关系式;在解答含有字母系数的一元二次方程问题时要弄清楚表示未知数的字母和待定系数的字母,正确运用根的判别式。这些问题一般最终转化为解方程或不等式的问题。
4 关于x的方程
有两个实数根,求k的取值范围。
解:原方程变形为:
若原方程有两个实数根,则有Δ≥0
这里的 a=k-1,b=-2(k-2),c=k+1.
即:
整理得:
-16k+20≥0
解得:
又 k-1≠0 即 k≠1
综合得:
且 k≠1
点评:一元二次方程隐含了二次项系数不为0,本题易忽略k-1≠o,所以解含字母系数的一元二次方程问题时要特别注意二次项系数是否为零。
第17章 一元二次方程根的判别式
1.一元二次方程的一般形式是_________
根的判别式是△=________
△___时 方程有 两个不相等 的实数根;
△___时 方程有 两个相等 的实数根;
△__时 方程无实数根。
<
<
> 0
<
= 0
< 0
知识归纳
求根公式
根的判别式
根的情况
2.一元二次方程根的判别式的应用
利用根的判别式解题大致有以下三种情况:
(1)a,b,c都是已知数,判断根的情况;
(2)a,b,c中含有字母,证明方程有无实数根。
(3)题中给出一元二次方程根的情况,求a,b,c待定系数的值或取值范围
1.不解方程,判断下列方程的根的情况:
(1)
(2)
(3)
所以原方程有两个不相等的实数根。
解:
解:
解:
所以原方程无实数根。
所以原方程有两个相等的实数根。
△=
△=
△=
这里a=3,b=10,c=3
这里 a=16,b=-8,c=1
这里 a=2,b=-3,c=2
应用举例
2.关于x的方程 一定有实数根吗?为什么?
解:原方程变形为:
△=
=
=
∴
原方程一定有实数根。
点评:若要使一元二次方程有实数根,则需这方程的根的判别式大于或等于0,即Δ≥0( )。
3. 当m取何值时,关于x的方程
(1)有两个不相等的实数根?
(2)有两个相等的实数根?
(3)无实数根?
解:△=
(1)当-4m+8>0时,
即m<2时,方程有两个不相等的实数根
(2)当-4m+8=0时,
即m=2时,方程有两个相等的实数根
(3)当-4m+8<0时,
即m>2时,方程无实数根
1.不解方程,判断下列关于x的方程的根的情况:
(1)
(2)
(3)
(4)
解:
原方程变形为:
解:
解:
原方程变形为:
△=
<0
△=
=0
所以原方程无实数根
所以原方程有两个相等的实数根
△=
=
≥0
解:
△=
所以原方程有两个实数根
当c=0时,△=0,方程有两个相等的实数根,
当a与c异号时,ac<0,则-4ac>0,即△>0,方程有两个不相等的实数根
当a与c同号时,ac>0,则-4ac<0,即△<0,方程没有实数根
=-4ac
试一试,你一定可以!
2.已知关于x的方程
k取何值时,此方程
(1)有两个实数根;(2)有实数根
解:
(1)因为方程有两个实数根,所以
△≥0
且 k+1≠0,
即:
{
k+1≠0
解得:
且 k≠-1
且 k≠-1
当 时,
方程有两个实数根.
(2) 当方程是一元一次方程时,即当k+1=0,k=-1时,方程为:
方程有一个实数根。
-2x+3=0,
当方程是关于x的一元二次方程时,k应满足
{
k+1≠0
且 k≠-1
解得:
综合 得:当 时,关于x的方程有实数根。
3 已知关于x的方程
有两个相等的实数根,求k的值及这时方程的根
解:
由题意得:
Δ=0 时,方程有两个相等的实数根。
解这个方程得: k1=2, k2=10
整理得:
原方程整理为:
即:
(1)当k=2时,原方程为:
解这个方程得 : x1=x2=
解这个方程得 : x3=x4=
(2)当k=10时,原方程为:
点评:在利用根的判别式解题时,一定要先把方程化为一般形式,确定了a,b,c,并正确算出
的值,然后根据判别式的取值与一元二次方程根的关系列出关系式;在解答含有字母系数的一元二次方程问题时要弄清楚表示未知数的字母和待定系数的字母,正确运用根的判别式。这些问题一般最终转化为解方程或不等式的问题。
4 关于x的方程
有两个实数根,求k的取值范围。
解:原方程变形为:
若原方程有两个实数根,则有Δ≥0
这里的 a=k-1,b=-2(k-2),c=k+1.
即:
整理得:
-16k+20≥0
解得:
又 k-1≠0 即 k≠1
综合得:
且 k≠1
点评:一元二次方程隐含了二次项系数不为0,本题易忽略k-1≠o,所以解含字母系数的一元二次方程问题时要特别注意二次项系数是否为零。
