浙江省桐乡市第一中学2011-2012学年高二上学期期中考试数学(理)试题
文档属性
| 名称 | 浙江省桐乡市第一中学2011-2012学年高二上学期期中考试数学(理)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 188.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-10 18:46:34 | ||
图片预览



文档简介
桐乡一中2011学年第一学期期中测试高二数学(理)试题卷
命题: __朱进初___
考生注意:1、考试范围:立体几何、空间向量、直线
2、总分分,时间分钟。
一、选择题:(本题共12题,每题3分,共36分)
1.直线的倾斜角是 ( )
A. B. C. D.
2.若右图是一个几何体的三视图,则这个几何体是 ( )
A.圆锥 B. 棱柱 C.圆柱 D.棱锥
3.若两异面直线互相垂直,且,则 ( )
A. B. C. D.
4.已知且,则与的位置关系是 ( )
A. B. C. D.
5.若平行于圆锥底面的平面将圆锥的高平分,则圆锥被分成的两部分的侧面积比是 ( )
A. 1:1 B. 1:2 C.1:3 D. 1:4
6.已知两直线和两平面,下列命题中正确的是 ( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
7.一水平放置的平面图形的直观图如图所示,则此平面图形的形状是 ( )
8.在正方体中,面对角线与所成角为 ( )
A. B. C. D.
9.在正方体中,为正方形中心,则与平面所
成角的正切值为 ( )
A. B. C. D.
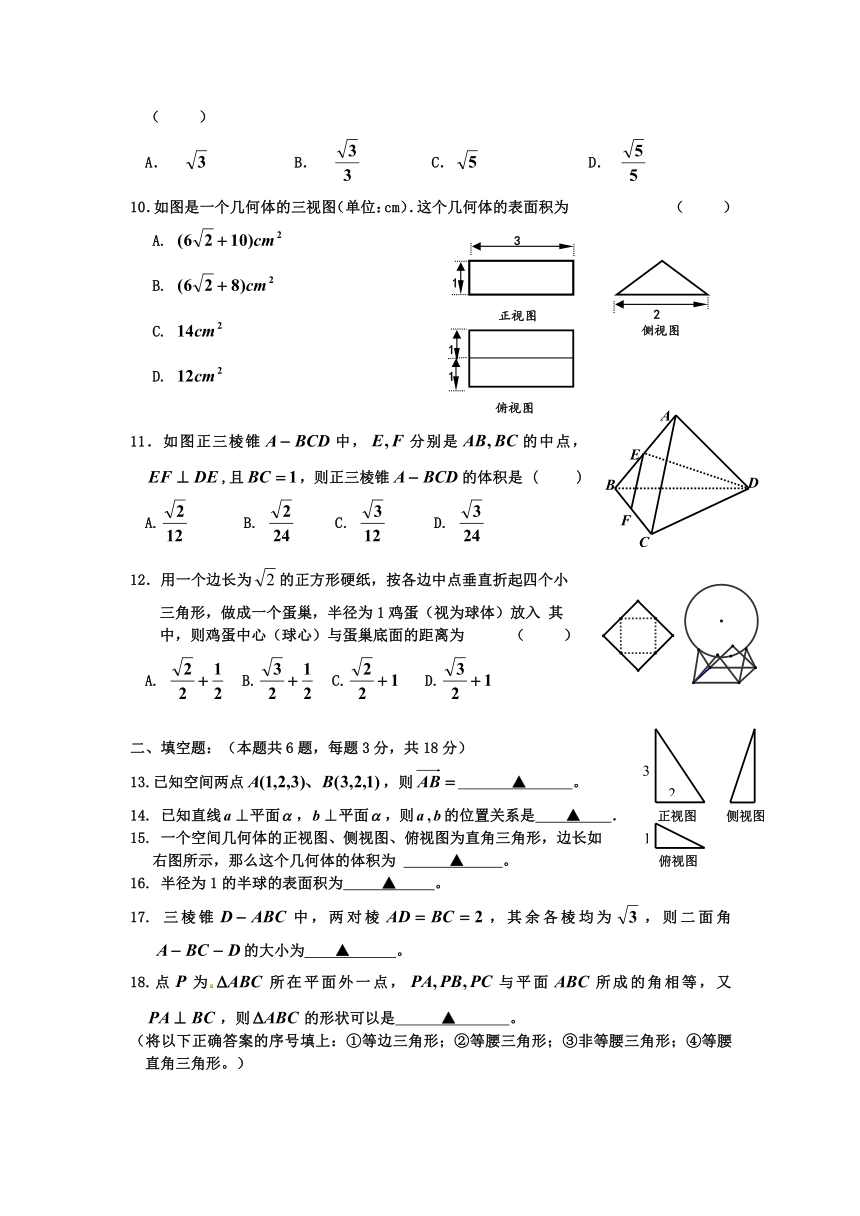
10.如图是一个几何体的三视图(单位:cm).这个几何体的表面积为 ( )
A.
B.
C.
D.
11.如图正三棱锥中,分别是的中点,,且,则正三棱锥的体积是 ( )
A. B. C. D.
12.用一个边长为的正方形硬纸,按各边中点垂直折起四个小
三角形,做成一个蛋巢,半径为1鸡蛋(视为球体)放入 其
中,则鸡蛋中心(球心)与蛋巢底面的距离为 ( )
A. B. C. D.
二、填空题:(本题共6题,每题3分,共18分)
13.已知空间两点,则 ▲ 。
14. 已知直线⊥平面,⊥平面,则,的位置关系是 ▲ .
15. 一个空间几何体的正视图、侧视图、俯视图为直角三角形,边长如
右图所示,那么这个几何体的体积为 ▲ 。
16. 半径为1的半球的表面积为 ▲ 。
17. 三棱锥中,两对棱,其余各棱均为,则二面角的大小为 ▲ 。
18.点为所在平面外一点,与平面所成的角相等,又,则的形状可以是 ▲ 。
(将以下正确答案的序号填上:①等边三角形;②等腰三角形;③非等腰三角形;④等腰直角三角形。)
三、解答题:(本题共6题,共46分)
19.(本题6分)已知直线。
(Ⅰ)当时,求直线的斜率;
(Ⅱ)若直线的倾斜角为,求范围。
20.(本题7分)已知三棱锥中,,,,且两两垂直,是中点,是重心,现如图建立空间直角坐标系。
(Ⅰ)求点和的坐标;
(Ⅱ)求异面直线和所成角的余弦值。
21.(本题7分)
如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,是的中点,是的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求证:;
(Ⅱ)求三棱锥的体积。
22.(本题8分)
如图四棱锥中,,,是的中点,是底面正方形的中心,。
(Ⅰ)求证:面;
(Ⅱ)求直线与平面所成的角。
23.(本题8分)
已知在四棱锥中,底面是矩形,且,,平面,分别是线段的中点。
(Ⅰ)证明:;
(Ⅱ)判断并说明上是否存在点,使得∥平面。
24.(本题10分)
如图,在直三棱柱中,,分别为的中点,四边形是边长为的正方形。
(Ⅰ)求证:平面;
(Ⅱ)求二面角的余弦值。
桐乡一中2011学年第一学期期中测试高二数学(理)
参考答案和评分标准
命题: ___朱进初_______
一、选择题:(本题共10题,每题2分,共20分。)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B C A D C A C C D B B A
二、填空题:(本题共6题,每题3分,共18分)
13、 (2,0,-2) 14、 平行
15、 1 16、
17、 18、 ①②④
三、解答题:(本题共6题,共46分)
19.(本题6分)已知直线。
(Ⅰ)当时,求直线的斜率; (Ⅱ)若直线的倾斜角为,求范围。
解:(Ⅰ)当时,; 3分
(Ⅱ)因为,
所以。 3分
20.(本题7分)已知三棱锥中,,,,且两两垂直,是中点,是重心,现如图建立空间直角坐标系。
(Ⅰ)求点和的坐标;
(Ⅱ)求异面直线和所成角的余弦值。
解:(Ⅰ)依题得,
所以。 3分
(Ⅱ) 1分
则 2分
所以异面直线和所成角的余弦值为。 1分
21.(本题7分)
如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,是的中点,是的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求证:;
(Ⅱ)求三棱锥的体积。
(Ⅰ)证明:,
又,
而
所以;
又是平行四边形,所以
因此。 4分
(Ⅱ)。 3分
22.(本题8分)
如图四棱锥中,,,是的中点,是底面正方形的中心,。
(Ⅰ)求证:面;
(Ⅱ)求直线与平面所成的角。
(Ⅰ)证明:
; 3分
(Ⅱ)解:
所以是与面所成角。 3分
在中,所以,
又,所以EO与平面所成的角为。 2分
23.(本题8分)
已知在四棱锥中,底面是矩形,且,,平面,分别是线段的中点。
(Ⅰ)证明:;
(Ⅱ)判断并说明上是否存在点,使得∥平面。
(Ⅰ)∵ 平面,,,,
建立如图所示的空间直角坐标系,
则. 2分
不妨令∵,
∴,即. 2分
(Ⅱ)设平面的法向量为,
由,得,令,解得:.∴. 2分
设点坐标为,,则,
要使∥平面,只需,即,
得,从而满足的点即为所求. 2分
24.(本题10分)
如图,在直三棱柱中,,分别为的中点,四边形是边长为的正方形。
(Ⅰ)求证:平面;
(Ⅱ)求二面角的余弦值。
(Ⅰ)证明: 在直三棱柱 HYPERLINK "http://www." 中,
平面,又平面 HYPERLINK "http://www." ,所以.
因为,为 HYPERLINK "http://www." 中点,所以.又,
所以平面 HYPERLINK "http://www." .又平面,所以 HYPERLINK "http://www." .
因为四边形为正方形,,分别为 HYPERLINK "http://www." ,的中点,所以△≌ HYPERLINK "http://www." △,.
所以.所以 HYPERLINK "http://www." EMBED Equation.DSMT4 。
又,所以平面 HYPERLINK "http://www." . 5分
(Ⅱ)解:如图,以的中点为原点,建立空间直角坐标系.
则.
由(2)知 HYPERLINK "http://www." 平面,所以为平面的一个法向量.
设为平面的一个法向量,
, HYPERLINK "http://www." .
由可得
令,则 HYPERLINK "http://www." .所以.
从而.
因为二面角为锐角,所以二面角 HYPERLINK "http://www." 的余弦值为. 5分
正视图
侧视图
俯视图
x/
y/
O/
A
B
C
D
俯视图
正视图
侧视图
3
1
1
1
2
D
A
E
F
C
B
1
3
2
俯视图
正视图
侧视图
A
B
C
D
O
E
S
E
P
D
F
C
B
A
E
D
C
B
A
A1
C1
B1
A
B
C
D
O
E
S
E
P
D
F
C
B
A
E
D
C
B
A
A1
C1
B1
命题: __朱进初___
考生注意:1、考试范围:立体几何、空间向量、直线
2、总分分,时间分钟。
一、选择题:(本题共12题,每题3分,共36分)
1.直线的倾斜角是 ( )
A. B. C. D.
2.若右图是一个几何体的三视图,则这个几何体是 ( )
A.圆锥 B. 棱柱 C.圆柱 D.棱锥
3.若两异面直线互相垂直,且,则 ( )
A. B. C. D.
4.已知且,则与的位置关系是 ( )
A. B. C. D.
5.若平行于圆锥底面的平面将圆锥的高平分,则圆锥被分成的两部分的侧面积比是 ( )
A. 1:1 B. 1:2 C.1:3 D. 1:4
6.已知两直线和两平面,下列命题中正确的是 ( )
A.若,,则 B.若,,则
C.若,,则 D.若,,则
7.一水平放置的平面图形的直观图如图所示,则此平面图形的形状是 ( )
8.在正方体中,面对角线与所成角为 ( )
A. B. C. D.
9.在正方体中,为正方形中心,则与平面所
成角的正切值为 ( )
A. B. C. D.
10.如图是一个几何体的三视图(单位:cm).这个几何体的表面积为 ( )
A.
B.
C.
D.
11.如图正三棱锥中,分别是的中点,,且,则正三棱锥的体积是 ( )
A. B. C. D.
12.用一个边长为的正方形硬纸,按各边中点垂直折起四个小
三角形,做成一个蛋巢,半径为1鸡蛋(视为球体)放入 其
中,则鸡蛋中心(球心)与蛋巢底面的距离为 ( )
A. B. C. D.
二、填空题:(本题共6题,每题3分,共18分)
13.已知空间两点,则 ▲ 。
14. 已知直线⊥平面,⊥平面,则,的位置关系是 ▲ .
15. 一个空间几何体的正视图、侧视图、俯视图为直角三角形,边长如
右图所示,那么这个几何体的体积为 ▲ 。
16. 半径为1的半球的表面积为 ▲ 。
17. 三棱锥中,两对棱,其余各棱均为,则二面角的大小为 ▲ 。
18.点为所在平面外一点,与平面所成的角相等,又,则的形状可以是 ▲ 。
(将以下正确答案的序号填上:①等边三角形;②等腰三角形;③非等腰三角形;④等腰直角三角形。)
三、解答题:(本题共6题,共46分)
19.(本题6分)已知直线。
(Ⅰ)当时,求直线的斜率;
(Ⅱ)若直线的倾斜角为,求范围。
20.(本题7分)已知三棱锥中,,,,且两两垂直,是中点,是重心,现如图建立空间直角坐标系。
(Ⅰ)求点和的坐标;
(Ⅱ)求异面直线和所成角的余弦值。
21.(本题7分)
如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,是的中点,是的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求证:;
(Ⅱ)求三棱锥的体积。
22.(本题8分)
如图四棱锥中,,,是的中点,是底面正方形的中心,。
(Ⅰ)求证:面;
(Ⅱ)求直线与平面所成的角。
23.(本题8分)
已知在四棱锥中,底面是矩形,且,,平面,分别是线段的中点。
(Ⅰ)证明:;
(Ⅱ)判断并说明上是否存在点,使得∥平面。
24.(本题10分)
如图,在直三棱柱中,,分别为的中点,四边形是边长为的正方形。
(Ⅰ)求证:平面;
(Ⅱ)求二面角的余弦值。
桐乡一中2011学年第一学期期中测试高二数学(理)
参考答案和评分标准
命题: ___朱进初_______
一、选择题:(本题共10题,每题2分,共20分。)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 B C A D C A C C D B B A
二、填空题:(本题共6题,每题3分,共18分)
13、 (2,0,-2) 14、 平行
15、 1 16、
17、 18、 ①②④
三、解答题:(本题共6题,共46分)
19.(本题6分)已知直线。
(Ⅰ)当时,求直线的斜率; (Ⅱ)若直线的倾斜角为,求范围。
解:(Ⅰ)当时,; 3分
(Ⅱ)因为,
所以。 3分
20.(本题7分)已知三棱锥中,,,,且两两垂直,是中点,是重心,现如图建立空间直角坐标系。
(Ⅰ)求点和的坐标;
(Ⅱ)求异面直线和所成角的余弦值。
解:(Ⅰ)依题得,
所以。 3分
(Ⅱ) 1分
则 2分
所以异面直线和所成角的余弦值为。 1分
21.(本题7分)
如图是某直三棱柱(侧棱与底面垂直的三棱柱)被削去上底后的直观图与三视图中的侧视图、俯视图,在直观图中,是的中点,是的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
(Ⅰ)求证:;
(Ⅱ)求三棱锥的体积。
(Ⅰ)证明:,
又,
而
所以;
又是平行四边形,所以
因此。 4分
(Ⅱ)。 3分
22.(本题8分)
如图四棱锥中,,,是的中点,是底面正方形的中心,。
(Ⅰ)求证:面;
(Ⅱ)求直线与平面所成的角。
(Ⅰ)证明:
; 3分
(Ⅱ)解:
所以是与面所成角。 3分
在中,所以,
又,所以EO与平面所成的角为。 2分
23.(本题8分)
已知在四棱锥中,底面是矩形,且,,平面,分别是线段的中点。
(Ⅰ)证明:;
(Ⅱ)判断并说明上是否存在点,使得∥平面。
(Ⅰ)∵ 平面,,,,
建立如图所示的空间直角坐标系,
则. 2分
不妨令∵,
∴,即. 2分
(Ⅱ)设平面的法向量为,
由,得,令,解得:.∴. 2分
设点坐标为,,则,
要使∥平面,只需,即,
得,从而满足的点即为所求. 2分
24.(本题10分)
如图,在直三棱柱中,,分别为的中点,四边形是边长为的正方形。
(Ⅰ)求证:平面;
(Ⅱ)求二面角的余弦值。
(Ⅰ)证明: 在直三棱柱 HYPERLINK "http://www." 中,
平面,又平面 HYPERLINK "http://www." ,所以.
因为,为 HYPERLINK "http://www." 中点,所以.又,
所以平面 HYPERLINK "http://www." .又平面,所以 HYPERLINK "http://www." .
因为四边形为正方形,,分别为 HYPERLINK "http://www." ,的中点,所以△≌ HYPERLINK "http://www." △,.
所以.所以 HYPERLINK "http://www." EMBED Equation.DSMT4 。
又,所以平面 HYPERLINK "http://www." . 5分
(Ⅱ)解:如图,以的中点为原点,建立空间直角坐标系.
则.
由(2)知 HYPERLINK "http://www." 平面,所以为平面的一个法向量.
设为平面的一个法向量,
, HYPERLINK "http://www." .
由可得
令,则 HYPERLINK "http://www." .所以.
从而.
因为二面角为锐角,所以二面角 HYPERLINK "http://www." 的余弦值为. 5分
正视图
侧视图
俯视图
x/
y/
O/
A
B
C
D
俯视图
正视图
侧视图
3
1
1
1
2
D
A
E
F
C
B
1
3
2
俯视图
正视图
侧视图
A
B
C
D
O
E
S
E
P
D
F
C
B
A
E
D
C
B
A
A1
C1
B1
A
B
C
D
O
E
S
E
P
D
F
C
B
A
E
D
C
B
A
A1
C1
B1
同课章节目录
