浙江省桐乡市第一中学2011-2012学年高二上学期期中考试数学(文)试题
文档属性
| 名称 | 浙江省桐乡市第一中学2011-2012学年高二上学期期中考试数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 162.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-10 18:46:34 | ||
图片预览



文档简介
桐乡一中2011学年第一学期期中测试高二(文)数学
试题卷
命题: __高丽君___
考生注意:1、考试范围:立体几何、直线
2、总分100分,时间120分钟。
一、选择题:(本题共12题,每题3分,共36分)
1.直线的倾斜角是
(A) (B) (C) (D)
2.右图是一个几何体的三视图,则这个几何体是
(A)圆锥 (B)棱柱 (C)圆柱 (D)棱锥
3.已知一个球的表面积为,则其体积为
(A) (B) (C) (D)
4.已知且,则与的位置关系是
(A) (B) (C) (D)
5.若平行于圆锥底面的平面将圆锥的高平分,则圆锥被分成的两部分的侧面积的比是
(A)1:1 (B)1:2 (C)1:3 (D)1:4
6.已知a、b是两条异面直线,c∥a,那么c与b的位置关系
(A)一定异面 (B)一定相交 (C)不可能平行 (D)不可能相交
7.一水平放置的平面图形的直观图如图所示,则此平面图形的形状是
8.在正方体中,面对角线与所成角为
(A) (B) (C) (D)
9.已知两直线和两平面,则下列命题中正确的是
(A)若,,则 (B)若,,则
(C)若,,则 (D)若,,则
10.如图是一个几何体的三视图(单位:cm).
则这个几何体的体积为
(A)6 cm2 (B)3 cm2
(C)2 cm2 (D)1 cm2
11.在正方体中,为正方形中心,则与平面ABCD所成角的正切值为
(A) (B) (C)1 (D)
12.两个完全相同的长方体的长、宽、高分别为5cm,4cm,3cm,把它们重叠在一起组成一个对角线最长的新长方体,则该最长对角线的长度是( )
(A)cm (B)cm (C)cm (D)cm
二、填空题:(本题共6题,每题3分,共18分)
13.已知点A(1,1)、B(0,2),则直线AB的斜率为 ▲ .
14.已知△ABC,直线⊥AB,⊥AC,则与BC所成的角的度数为 ▲ .
15.等边三角形的边长为2,绕着它的高旋转一周所得几何体的表面积是 ▲ .
16.已知球的半径为2,它被一个与球心距离为1的平面所截,则截面的面积是 ▲ .
17.三棱锥中,两对棱,其余各棱长均为,则二面角的大小为 ▲ .
18. Rt△ABC的斜边在平面内,直角顶点C是外一点,AC、BC与所成角分别为30°和45°,则平面ABC与所成锐角为 ▲ .
三、解答题:(本题共6题,共46分)
19.(本题6分)已知直线。
(Ⅰ)当时,求直线的斜率;
(Ⅱ)若直线的倾斜角为,求范围。
20.(本题满分6分)如图,四面体ABCD中,AD⊥平面BCD,E、F分别为AB、AC的中点,.求证: EF⊥平面ACD.
21.(本题8分)如图,ABCD-A1B1C1D1是棱长为的正方体.
(Ⅰ)求异面直线BD1与AA1所成的角的余弦值;
(Ⅱ)求三棱锥A1-BCD的体积.
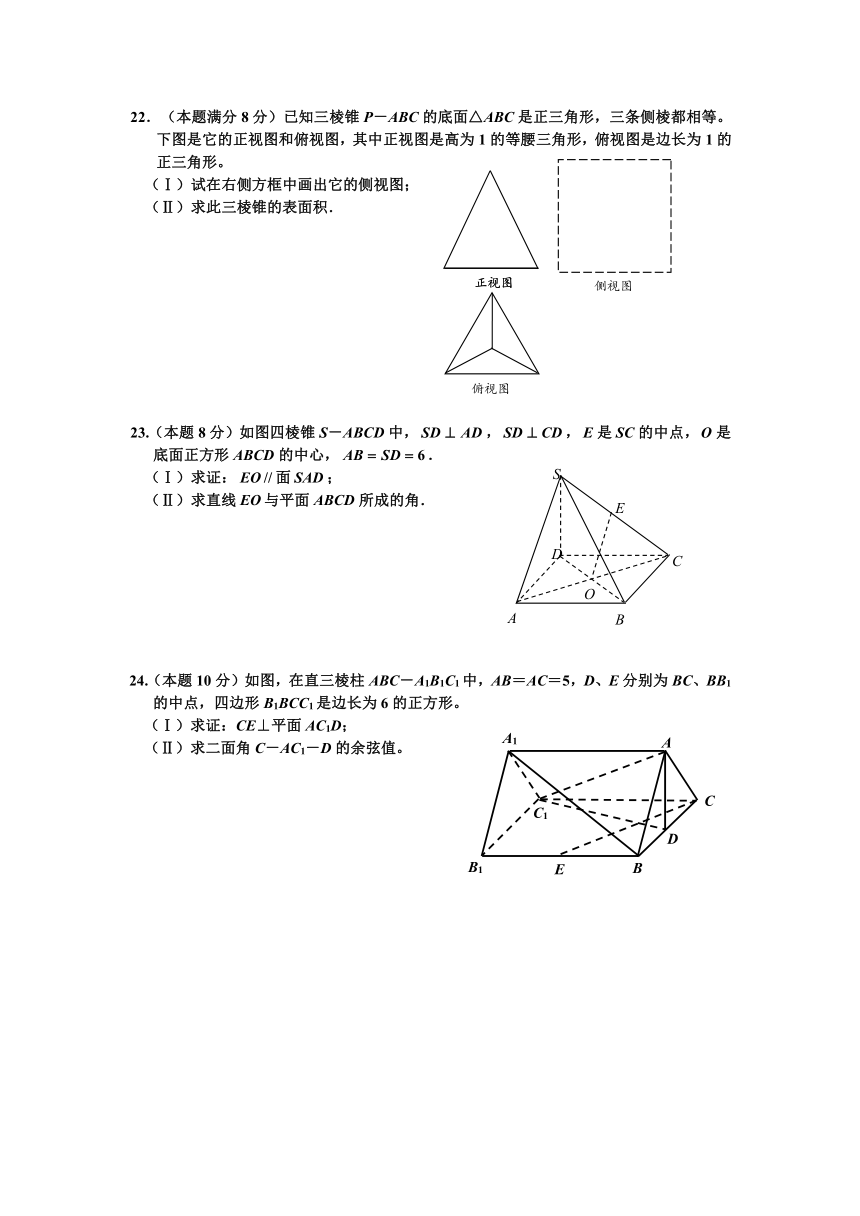
22.(本题满分8分)已知三棱锥P-ABC的底面△ABC是正三角形,三条侧棱都相等。下图是它的正视图和俯视图,其中正视图是高为1的等腰三角形,俯视图是边长为1的正三角形。
(Ⅰ)试在右侧方框中画出它的侧视图;
(Ⅱ)求此三棱锥的表面积.
23.(本题8分)如图四棱锥S-ABCD中,,,是的中点,是底面正方形的中心,.
(Ⅰ)求证:面;
(Ⅱ)求直线与平面所成的角.
24.(本题10分)如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D、E分别为BC、BB1的中点,四边形B1BCC1是边长为6的正方形。
(Ⅰ)求证:CE⊥平面AC1D;
(Ⅱ)求二面角C-AC1-D的余弦值。
桐乡一中2011学年第一学期期中测试高二(文)数学
参考答案和评分标准
命题: ___高丽君___
选择题:(本题共10题,每题2分,共20分。)
二、填空题:(本题共6题,每题3分,共18分)
13、-1 14、 15、3
16、 17、 18、
三、解答题:(本题共6题,共46分)
19.(本题6分)已知直线。
(Ⅰ)当时,求直线的斜率;
(Ⅱ)若直线的倾斜角为,求范围。
解:(Ⅰ)当时,; …………………………… 3分
(Ⅱ)因为,
所以。 …………………………… 3分
20、因为AD⊥平面BCD,所以AD⊥BC, ………………………………1分
又
而ADCD=D,故BC⊥平面ACD, ………………………………3分
因为E、F分别为AB、AC的中点,所以EF∥BC,
所以EF⊥平面ACD. ………………………………2分
21、(1)因为DD1∥AA1,故∠DD1B就是异面直线BD1与AA1所成的角 ……………2分
在Rt△DD1B中,DD1=a,BD=a,所以BD1=a,
所以cos∠DD1B== ………………………………3分
(2)V==………………………………3分
23.(本题8分)
如图四棱锥中,,,是的中点,是底面正方形的中心,。
(Ⅰ)求证:面;
(Ⅱ)求直线与平面所成的角。
(Ⅰ)证明:
; 3分
(Ⅱ)解:
所以是与面所成角。 3分
在中,所以,
又,所以EO与平面所成的角为。 2分
24.(本题10分)
如图,在直三棱柱中,,分别为的中点,四边形是边长为的正方形。
(Ⅰ)求证:平面;
(Ⅱ)求二面角的余弦值。
(Ⅰ)证明: 在直三棱柱中,
平面 HYPERLINK "http://www." ,又平面,所以.
因为 HYPERLINK "http://www." ,为中点,所以.又 HYPERLINK "http://www." ,
所以平面.又平面 HYPERLINK "http://www." ,所以.
因为四边形为正方形, HYPERLINK "http://www." ,分别为,的中点,所以 HYPERLINK "http://www." △≌△, HYPERLINK "http://www." .
所以.所以。
又 HYPERLINK "http://www." ,所以平面. 5分
(Ⅱ)解法一:过C作CG⊥AC1于G,记C1D与CE的交点为H,连结GH,
由(1)知,CH⊥平面AC1D,得CH⊥AC1,
CGCH=C,所以AC1⊥平面CGH,
所以AC1⊥GH,
故∠CGH就是二面角C-AC1-D的平面角,
在Rt△C1CA中,计算得CG=,
在Rt△C1CD中,计算得CH=,
所以在Rt△CHG中,sin∠CGH=,
故cos∠CGH= ……………………………5分
解法二:如图,以 HYPERLINK "http://www." 的中点为原点,建立空间直角坐标系.
则.
由(2)知平面 HYPERLINK "http://www." ,所以为平面的一个法向量.
设 HYPERLINK "http://www." 为平面的一个法向量,
,.
由 HYPERLINK "http://www." 可得
令,则.所以 HYPERLINK "http://www." .
从而.
因为二面角为锐角,所以二面角的余弦值为 HYPERLINK "http://www." . 5分
正视图
侧视图
俯视图
x/
y/
O/
(A)
(B)
(C)
(D)
俯视图
正视图
侧视图
3
1
1
1
2
B
A
D
C
E
F
侧视图
正视图
俯视图
正视图
A
B
C
D
O
E
S
A
A1
B1
B
C1
C
D
E
B
A
D
C
E
F
A
B
C
D
O
E
S
A
A1
B1
B
C1
C
D
E
G
H
试题卷
命题: __高丽君___
考生注意:1、考试范围:立体几何、直线
2、总分100分,时间120分钟。
一、选择题:(本题共12题,每题3分,共36分)
1.直线的倾斜角是
(A) (B) (C) (D)
2.右图是一个几何体的三视图,则这个几何体是
(A)圆锥 (B)棱柱 (C)圆柱 (D)棱锥
3.已知一个球的表面积为,则其体积为
(A) (B) (C) (D)
4.已知且,则与的位置关系是
(A) (B) (C) (D)
5.若平行于圆锥底面的平面将圆锥的高平分,则圆锥被分成的两部分的侧面积的比是
(A)1:1 (B)1:2 (C)1:3 (D)1:4
6.已知a、b是两条异面直线,c∥a,那么c与b的位置关系
(A)一定异面 (B)一定相交 (C)不可能平行 (D)不可能相交
7.一水平放置的平面图形的直观图如图所示,则此平面图形的形状是
8.在正方体中,面对角线与所成角为
(A) (B) (C) (D)
9.已知两直线和两平面,则下列命题中正确的是
(A)若,,则 (B)若,,则
(C)若,,则 (D)若,,则
10.如图是一个几何体的三视图(单位:cm).
则这个几何体的体积为
(A)6 cm2 (B)3 cm2
(C)2 cm2 (D)1 cm2
11.在正方体中,为正方形中心,则与平面ABCD所成角的正切值为
(A) (B) (C)1 (D)
12.两个完全相同的长方体的长、宽、高分别为5cm,4cm,3cm,把它们重叠在一起组成一个对角线最长的新长方体,则该最长对角线的长度是( )
(A)cm (B)cm (C)cm (D)cm
二、填空题:(本题共6题,每题3分,共18分)
13.已知点A(1,1)、B(0,2),则直线AB的斜率为 ▲ .
14.已知△ABC,直线⊥AB,⊥AC,则与BC所成的角的度数为 ▲ .
15.等边三角形的边长为2,绕着它的高旋转一周所得几何体的表面积是 ▲ .
16.已知球的半径为2,它被一个与球心距离为1的平面所截,则截面的面积是 ▲ .
17.三棱锥中,两对棱,其余各棱长均为,则二面角的大小为 ▲ .
18. Rt△ABC的斜边在平面内,直角顶点C是外一点,AC、BC与所成角分别为30°和45°,则平面ABC与所成锐角为 ▲ .
三、解答题:(本题共6题,共46分)
19.(本题6分)已知直线。
(Ⅰ)当时,求直线的斜率;
(Ⅱ)若直线的倾斜角为,求范围。
20.(本题满分6分)如图,四面体ABCD中,AD⊥平面BCD,E、F分别为AB、AC的中点,.求证: EF⊥平面ACD.
21.(本题8分)如图,ABCD-A1B1C1D1是棱长为的正方体.
(Ⅰ)求异面直线BD1与AA1所成的角的余弦值;
(Ⅱ)求三棱锥A1-BCD的体积.
22.(本题满分8分)已知三棱锥P-ABC的底面△ABC是正三角形,三条侧棱都相等。下图是它的正视图和俯视图,其中正视图是高为1的等腰三角形,俯视图是边长为1的正三角形。
(Ⅰ)试在右侧方框中画出它的侧视图;
(Ⅱ)求此三棱锥的表面积.
23.(本题8分)如图四棱锥S-ABCD中,,,是的中点,是底面正方形的中心,.
(Ⅰ)求证:面;
(Ⅱ)求直线与平面所成的角.
24.(本题10分)如图,在直三棱柱ABC-A1B1C1中,AB=AC=5,D、E分别为BC、BB1的中点,四边形B1BCC1是边长为6的正方形。
(Ⅰ)求证:CE⊥平面AC1D;
(Ⅱ)求二面角C-AC1-D的余弦值。
桐乡一中2011学年第一学期期中测试高二(文)数学
参考答案和评分标准
命题: ___高丽君___
选择题:(本题共10题,每题2分,共20分。)
二、填空题:(本题共6题,每题3分,共18分)
13、-1 14、 15、3
16、 17、 18、
三、解答题:(本题共6题,共46分)
19.(本题6分)已知直线。
(Ⅰ)当时,求直线的斜率;
(Ⅱ)若直线的倾斜角为,求范围。
解:(Ⅰ)当时,; …………………………… 3分
(Ⅱ)因为,
所以。 …………………………… 3分
20、因为AD⊥平面BCD,所以AD⊥BC, ………………………………1分
又
而ADCD=D,故BC⊥平面ACD, ………………………………3分
因为E、F分别为AB、AC的中点,所以EF∥BC,
所以EF⊥平面ACD. ………………………………2分
21、(1)因为DD1∥AA1,故∠DD1B就是异面直线BD1与AA1所成的角 ……………2分
在Rt△DD1B中,DD1=a,BD=a,所以BD1=a,
所以cos∠DD1B== ………………………………3分
(2)V==………………………………3分
23.(本题8分)
如图四棱锥中,,,是的中点,是底面正方形的中心,。
(Ⅰ)求证:面;
(Ⅱ)求直线与平面所成的角。
(Ⅰ)证明:
; 3分
(Ⅱ)解:
所以是与面所成角。 3分
在中,所以,
又,所以EO与平面所成的角为。 2分
24.(本题10分)
如图,在直三棱柱中,,分别为的中点,四边形是边长为的正方形。
(Ⅰ)求证:平面;
(Ⅱ)求二面角的余弦值。
(Ⅰ)证明: 在直三棱柱中,
平面 HYPERLINK "http://www." ,又平面,所以.
因为 HYPERLINK "http://www." ,为中点,所以.又 HYPERLINK "http://www." ,
所以平面.又平面 HYPERLINK "http://www." ,所以.
因为四边形为正方形, HYPERLINK "http://www." ,分别为,的中点,所以 HYPERLINK "http://www." △≌△, HYPERLINK "http://www." .
所以.所以。
又 HYPERLINK "http://www." ,所以平面. 5分
(Ⅱ)解法一:过C作CG⊥AC1于G,记C1D与CE的交点为H,连结GH,
由(1)知,CH⊥平面AC1D,得CH⊥AC1,
CGCH=C,所以AC1⊥平面CGH,
所以AC1⊥GH,
故∠CGH就是二面角C-AC1-D的平面角,
在Rt△C1CA中,计算得CG=,
在Rt△C1CD中,计算得CH=,
所以在Rt△CHG中,sin∠CGH=,
故cos∠CGH= ……………………………5分
解法二:如图,以 HYPERLINK "http://www." 的中点为原点,建立空间直角坐标系.
则.
由(2)知平面 HYPERLINK "http://www." ,所以为平面的一个法向量.
设 HYPERLINK "http://www." 为平面的一个法向量,
,.
由 HYPERLINK "http://www." 可得
令,则.所以 HYPERLINK "http://www." .
从而.
因为二面角为锐角,所以二面角的余弦值为 HYPERLINK "http://www." . 5分
正视图
侧视图
俯视图
x/
y/
O/
(A)
(B)
(C)
(D)
俯视图
正视图
侧视图
3
1
1
1
2
B
A
D
C
E
F
侧视图
正视图
俯视图
正视图
A
B
C
D
O
E
S
A
A1
B1
B
C1
C
D
E
B
A
D
C
E
F
A
B
C
D
O
E
S
A
A1
B1
B
C1
C
D
E
G
H
同课章节目录
