青岛(六三)版数学四上 6.快捷的物流运输--解决问题 教案
文档属性
| 名称 | 青岛(六三)版数学四上 6.快捷的物流运输--解决问题 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 348.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 00:00:00 | ||
图片预览



文档简介
速度、时间和路程
[教学目标]
1.结合具体情境,理解速度、时间、路程的含义,掌握三者之间的数量关系,并学会应用这种关系解决实际问题。
2.经历从实际问题中抽象出“速度、时间、路程”概念和建构三者关系模型的过程,发展学生的抽象能力,初步渗透模型思想。
3.在发现问题、提出问题、分析问题、解决问题的过程中,培养问题解决意识,在合作交流中体验学习的乐趣,在实际应用中培养应用意识和创新意识。
[教学重点] 理清路程、时间与速度之间的数量关系,构建行程问题模型。
[教学难点]理解速度的概念以及速度、时间、路程三者的数量关系模型背后的意义。
[教学过程]
一、创设情境,提出问题
课前谈话,师:我们所购买的商品是怎样来到我们手中的呢?
预设:学生根据生活经验可能会谈到快递、邮局邮递等等。
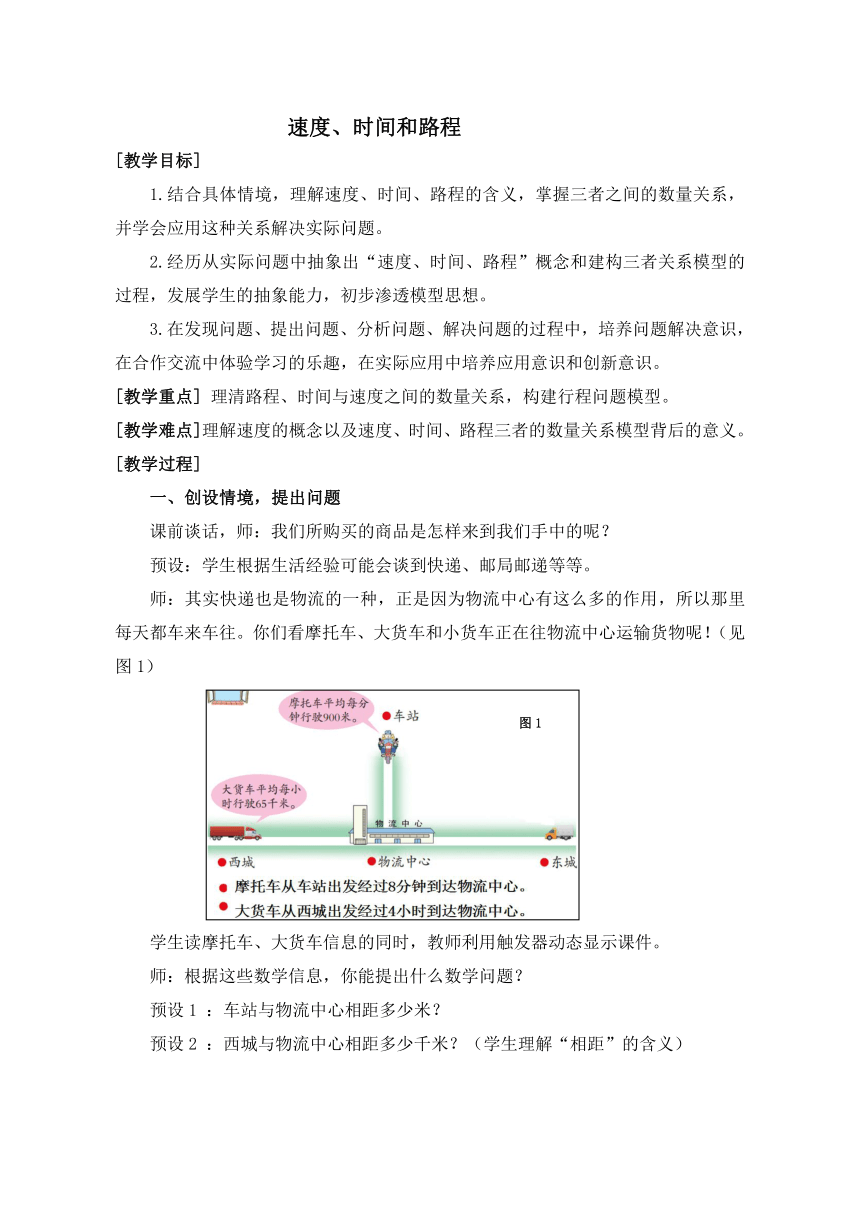
师:其实快递也是物流的一种,正是因为物流中心有这么多的作用,所以那里每天都车来车往。你们看摩托车、大货车和小货车正在往物流中心运输货物呢!(见图1)
学生读摩托车、大货车信息的同时,教师利用触发器动态显示课件。
师:根据这些数学信息,你能提出什么数学问题?
预设1 :车站与物流中心相距多少米?
预设2 :西城与物流中心相距多少千米?(学生理解“相距”的含义)
【设计意图】学生在生活中所接触的有关物流方面最多的应该就是网上购物了,教师以谈话的方式,轻松地创设了有关物流的情景,引导学生发现信息、提出问题。学生了解了物流中心,头脑中再现车辆运动的现象,为接下来探索新知起到了很好的铺垫作用。
二、独立解决问题
学生独自解决问题1、2
师:仔细读题,同学们独自来解决这个问题,并同桌分享自己的方法。
学生汇报并板书:900×8=7200(米) 65×4=260(千米)
学生探究算式中每个数字代表的含义并板书
预设1 : 平均每分钟行驶900 米,走了8 分钟到物流中心,所以就是900×8 。
预设2 :900 是每分钟行驶的米数,8 是表示行驶了8 分钟,900×8 就表示一共行驶了多少米。
板书:每分钟行驶的米数×行驶的分钟数=车站到物流中心的米数
师:如果我用一条线段表示从车站到物流中心的距离。(见图2)
动
师:8 分钟行驶了8 个900 米,所以算式是900×8或者8×900。
师:你能像上一个题一样把这个问题的关系式也说一说吗?
板书:每小时行驶的千米数×行驶的小时数=西城到物流中心的千米数
【设计意图】借助已有的生活和学习经验独立列出算式并全面分析其中具体的数量关系式,为后面抽象三个数量及它们之间的关系打好基础。同时,借助线段图呈现三个数量之间的关系,直观、形象,易于理解,有助于分析解决问题,也会为下面相遇问题模型的建立打下良好基础。
三、抽象概括,建立基本数量关系模型
(一)抽象概括,提炼概念
师:仔细观察这两个关系式,你能用更简洁的语言来表示每个数字吗?
预设:“路程”指的是车站到物流中心的米数和西城到物流中心的千米数。
“时间”指的是8分钟、4小时。
“速度”:每分钟行驶900 米,每小时行驶65千米。
师:数学上,我们把从车站、西城到物流中心的米数这种表示从行驶起点到终点的行驶路线的长度,叫“路程”。
师:每分钟、每小时我们叫单位时间,你还知道哪些单位时间?
预设:每秒、每天、每月、每周……
师:像每秒、每天、每月、每周……这样的时间都叫做单位时间,那单位时间内行驶的路程就叫速度。
(二)认识速度
1.读写。
师:以“每分钟行驶900 米”大货车的速度为例,写作:900米/分, 读作:900米每分。会了吗?老师考考你!
(1)你会读吗?
声音传播的速度大约为340米/秒。
光传播的速度大约为30万千米/秒。
(2)你会写吗?
1.兔子5秒跑了50米,兔子的奔跑速度是(10米/秒 )
2.乌龟3分爬了30米,乌龟爬行的速度是( 10米/分)
师:你认为乌龟和兔子跑的一样快吗?
(3)你会判断吗?
①李老师骑自行车行驶了15千米,这里的15千米表示的是李老师骑自行车的速度。
(三)推理另外两个数量关系式
1.师:刚才这两道题都是知道了速度和时间,求路程因此我们得到速度×时间=路程,现在老师把摩托车的问题和条件换一换,你还能解决吗?。你能推想出速度、时间、路程哪些数量关系呢?
2.自主学习,小组探究。
探究提示:
第一步:观察信息。
结合所提的问题寻找需要的信息,并结合信息,思考解决问题的方法。
第二步:独立思考。
根据理解,借助刚才的知识与方法动脑思考,理清数量关系,寻求解决方案。
第三步:合作交流。
小组内共同分析出速度、时间和路程三者的关系式
3.投影展示
小组成员汇报补充,其他同学提出疑问。理清数量关系
路程÷时间=速度
路程÷速度=时间
速度×时间=路程
师:这节课我们认识了速度、时间与路程,知道它们三者之间有着密切的关系,这就是我们今天所研究的主要内容: 速度、时间与路程。
板书课题:速度、时间、路程
【设计意图】充分放手学生通过观察、对比、思考、提炼、概括等活动,抽象概括出新的数量关系“路程÷时间=速度 、 路程÷速度=时间”。解决问题的过程,即学生在头脑中建立数学模型的过程,培养其推理能力,渗透模型思想。
四、巩固应用,拓展提高
师:我们已经成功的解决了物流中心的问题,接下来我要考考你
1.出示苏炳添的视频,感知中国速度。
通过学生对比两个表格总结得出:
路程相同比时间,时间越短,速度越快。
时间相同比路程,路程越长,速度越快。
总结:田径项目一直以来是我国的弱项,通过我们国人的努力,也一次次突破记录,走向世界。学习也是一样的,要有毅力恒心。
师:丽丽和乐乐在争论谁跑的快?请你思考
引导学生理解“什么是走的快”“求速度和谁有关”
3.
学生读题,理解题意,引领分析。独立完成,说出速度、时间和路程的关系再计算,集体交流。
4. 带有这个标志的路共长140千米,张叔叔驾车想花2小时开完这一路段。他会超速吗? (限速60千米/时)
学生读题,理解题意,引领分析,利用速度、时间和路程的关系独立完成。学生互相评价质疑,鼓励多种解题思路。并说出“你想对张叔叔说些什么?”
全课总结,拓展延伸
1.这节课你有什么收获?(适时点评)
师:是啊,其实我们今天所学习的数量关系不仅仅可以用在行程问题中,还可以用在我们生活中的很多问题中,是吧?希望你带着一双善于发现的眼睛,继续去观察和思考生活中的数学问题!
2.学生读一读“苏炳添、高铁、歼-20、“墨子号””感知我们引以为豪的中国速度
【设计意图】练习的设计从易到难、层层递进,紧紧围绕教学目标的落实进行了有效的设计,在检验学生时知识是否掌握的同时,又让学生的思维有了新的升华。学生通过观察、讨论发现出来的内容往往令我们惊叹。其实这一个环节也培养了学生的迁移能力。
[教学目标]
1.结合具体情境,理解速度、时间、路程的含义,掌握三者之间的数量关系,并学会应用这种关系解决实际问题。
2.经历从实际问题中抽象出“速度、时间、路程”概念和建构三者关系模型的过程,发展学生的抽象能力,初步渗透模型思想。
3.在发现问题、提出问题、分析问题、解决问题的过程中,培养问题解决意识,在合作交流中体验学习的乐趣,在实际应用中培养应用意识和创新意识。
[教学重点] 理清路程、时间与速度之间的数量关系,构建行程问题模型。
[教学难点]理解速度的概念以及速度、时间、路程三者的数量关系模型背后的意义。
[教学过程]
一、创设情境,提出问题
课前谈话,师:我们所购买的商品是怎样来到我们手中的呢?
预设:学生根据生活经验可能会谈到快递、邮局邮递等等。
师:其实快递也是物流的一种,正是因为物流中心有这么多的作用,所以那里每天都车来车往。你们看摩托车、大货车和小货车正在往物流中心运输货物呢!(见图1)
学生读摩托车、大货车信息的同时,教师利用触发器动态显示课件。
师:根据这些数学信息,你能提出什么数学问题?
预设1 :车站与物流中心相距多少米?
预设2 :西城与物流中心相距多少千米?(学生理解“相距”的含义)
【设计意图】学生在生活中所接触的有关物流方面最多的应该就是网上购物了,教师以谈话的方式,轻松地创设了有关物流的情景,引导学生发现信息、提出问题。学生了解了物流中心,头脑中再现车辆运动的现象,为接下来探索新知起到了很好的铺垫作用。
二、独立解决问题
学生独自解决问题1、2
师:仔细读题,同学们独自来解决这个问题,并同桌分享自己的方法。
学生汇报并板书:900×8=7200(米) 65×4=260(千米)
学生探究算式中每个数字代表的含义并板书
预设1 : 平均每分钟行驶900 米,走了8 分钟到物流中心,所以就是900×8 。
预设2 :900 是每分钟行驶的米数,8 是表示行驶了8 分钟,900×8 就表示一共行驶了多少米。
板书:每分钟行驶的米数×行驶的分钟数=车站到物流中心的米数
师:如果我用一条线段表示从车站到物流中心的距离。(见图2)
动
师:8 分钟行驶了8 个900 米,所以算式是900×8或者8×900。
师:你能像上一个题一样把这个问题的关系式也说一说吗?
板书:每小时行驶的千米数×行驶的小时数=西城到物流中心的千米数
【设计意图】借助已有的生活和学习经验独立列出算式并全面分析其中具体的数量关系式,为后面抽象三个数量及它们之间的关系打好基础。同时,借助线段图呈现三个数量之间的关系,直观、形象,易于理解,有助于分析解决问题,也会为下面相遇问题模型的建立打下良好基础。
三、抽象概括,建立基本数量关系模型
(一)抽象概括,提炼概念
师:仔细观察这两个关系式,你能用更简洁的语言来表示每个数字吗?
预设:“路程”指的是车站到物流中心的米数和西城到物流中心的千米数。
“时间”指的是8分钟、4小时。
“速度”:每分钟行驶900 米,每小时行驶65千米。
师:数学上,我们把从车站、西城到物流中心的米数这种表示从行驶起点到终点的行驶路线的长度,叫“路程”。
师:每分钟、每小时我们叫单位时间,你还知道哪些单位时间?
预设:每秒、每天、每月、每周……
师:像每秒、每天、每月、每周……这样的时间都叫做单位时间,那单位时间内行驶的路程就叫速度。
(二)认识速度
1.读写。
师:以“每分钟行驶900 米”大货车的速度为例,写作:900米/分, 读作:900米每分。会了吗?老师考考你!
(1)你会读吗?
声音传播的速度大约为340米/秒。
光传播的速度大约为30万千米/秒。
(2)你会写吗?
1.兔子5秒跑了50米,兔子的奔跑速度是(10米/秒 )
2.乌龟3分爬了30米,乌龟爬行的速度是( 10米/分)
师:你认为乌龟和兔子跑的一样快吗?
(3)你会判断吗?
①李老师骑自行车行驶了15千米,这里的15千米表示的是李老师骑自行车的速度。
(三)推理另外两个数量关系式
1.师:刚才这两道题都是知道了速度和时间,求路程因此我们得到速度×时间=路程,现在老师把摩托车的问题和条件换一换,你还能解决吗?。你能推想出速度、时间、路程哪些数量关系呢?
2.自主学习,小组探究。
探究提示:
第一步:观察信息。
结合所提的问题寻找需要的信息,并结合信息,思考解决问题的方法。
第二步:独立思考。
根据理解,借助刚才的知识与方法动脑思考,理清数量关系,寻求解决方案。
第三步:合作交流。
小组内共同分析出速度、时间和路程三者的关系式
3.投影展示
小组成员汇报补充,其他同学提出疑问。理清数量关系
路程÷时间=速度
路程÷速度=时间
速度×时间=路程
师:这节课我们认识了速度、时间与路程,知道它们三者之间有着密切的关系,这就是我们今天所研究的主要内容: 速度、时间与路程。
板书课题:速度、时间、路程
【设计意图】充分放手学生通过观察、对比、思考、提炼、概括等活动,抽象概括出新的数量关系“路程÷时间=速度 、 路程÷速度=时间”。解决问题的过程,即学生在头脑中建立数学模型的过程,培养其推理能力,渗透模型思想。
四、巩固应用,拓展提高
师:我们已经成功的解决了物流中心的问题,接下来我要考考你
1.出示苏炳添的视频,感知中国速度。
通过学生对比两个表格总结得出:
路程相同比时间,时间越短,速度越快。
时间相同比路程,路程越长,速度越快。
总结:田径项目一直以来是我国的弱项,通过我们国人的努力,也一次次突破记录,走向世界。学习也是一样的,要有毅力恒心。
师:丽丽和乐乐在争论谁跑的快?请你思考
引导学生理解“什么是走的快”“求速度和谁有关”
3.
学生读题,理解题意,引领分析。独立完成,说出速度、时间和路程的关系再计算,集体交流。
4. 带有这个标志的路共长140千米,张叔叔驾车想花2小时开完这一路段。他会超速吗? (限速60千米/时)
学生读题,理解题意,引领分析,利用速度、时间和路程的关系独立完成。学生互相评价质疑,鼓励多种解题思路。并说出“你想对张叔叔说些什么?”
全课总结,拓展延伸
1.这节课你有什么收获?(适时点评)
师:是啊,其实我们今天所学习的数量关系不仅仅可以用在行程问题中,还可以用在我们生活中的很多问题中,是吧?希望你带着一双善于发现的眼睛,继续去观察和思考生活中的数学问题!
2.学生读一读“苏炳添、高铁、歼-20、“墨子号””感知我们引以为豪的中国速度
【设计意图】练习的设计从易到难、层层递进,紧紧围绕教学目标的落实进行了有效的设计,在检验学生时知识是否掌握的同时,又让学生的思维有了新的升华。学生通过观察、讨论发现出来的内容往往令我们惊叹。其实这一个环节也培养了学生的迁移能力。
