人教高中数学必修五 3.2一元二次不等式及其解法 课件(16张ppt)
文档属性
| 名称 | 人教高中数学必修五 3.2一元二次不等式及其解法 课件(16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 563.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-12 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
3.2
一元二次不等式及其解法
(第一课时)
制作一个高为2m的长方体容器,底面矩形的长比宽少1m,并且长方体的容积大于12m3,问底面矩形的宽的取值范围?
新课引入
x2-x-6>0
一元二次不等式(定义)
新知讲解
那么怎样求一元二次不等式
x2-x-6>0的解集呢?
一个
2
x2-x-6>0
像
这样只含
未知数,并且未知数最高次数为
的不等式,称为一元二次不等式.
像
这样只含
未知数,并且未知数最高次数为
的不等式,称为一元二次不等式.
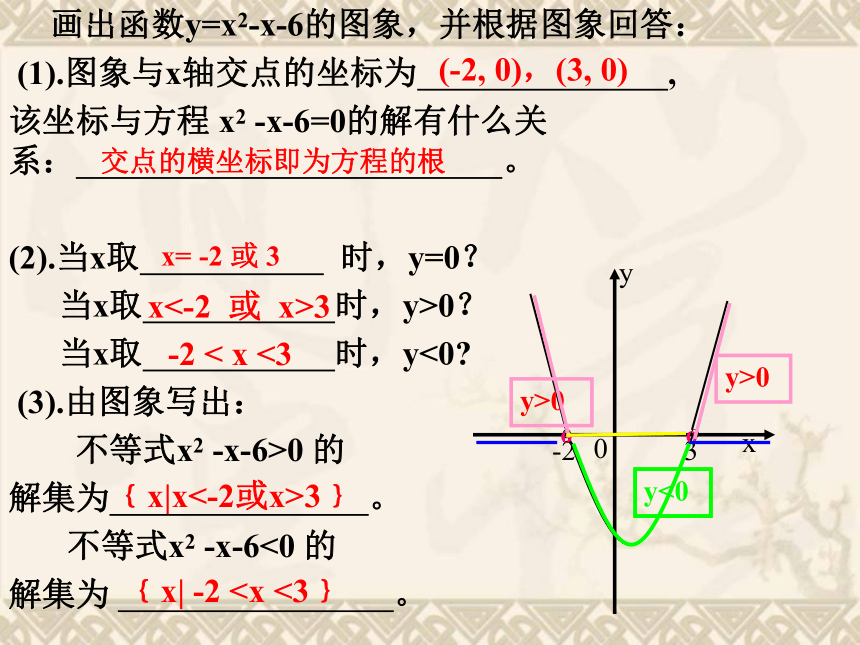
画出函数y=x2-x-6的图象,并根据图象回答:
(1).图象与x轴交点的坐标为
,
该坐标与方程
x2
-x-6=0的解有什么关系:
。
(2).当x取
时,y=0?
当x取
时,y>0?
当x取
时,y<0?
(3).由图象写出:
不等式x2
-x-6>0
的
解集为
。
不等式x2
-x-6<0
的
解集为
。
(-2,
0),(3,
0)
交点的横坐标即为方程的根
x=
-2
或
3
x<-2
或
x>3
-2
<
x
<3
﹛x|x<-2或x>3﹜
﹛x|
-2
<3﹜
y
x
0
-2
3
o
o
o
o
y>0
y>0
y<0
方程
ax2+bx+c=0、
不等式ax2+bx+c>0、
或ax2+bx+c<0
与函数y=
ax2+bx+c>0的图象有什么关系?
思考:
结论:方程的解即函数图象与x轴交点的横坐标,不等式的解集即函数图象在x轴上方或下方图象所对应x的范围。
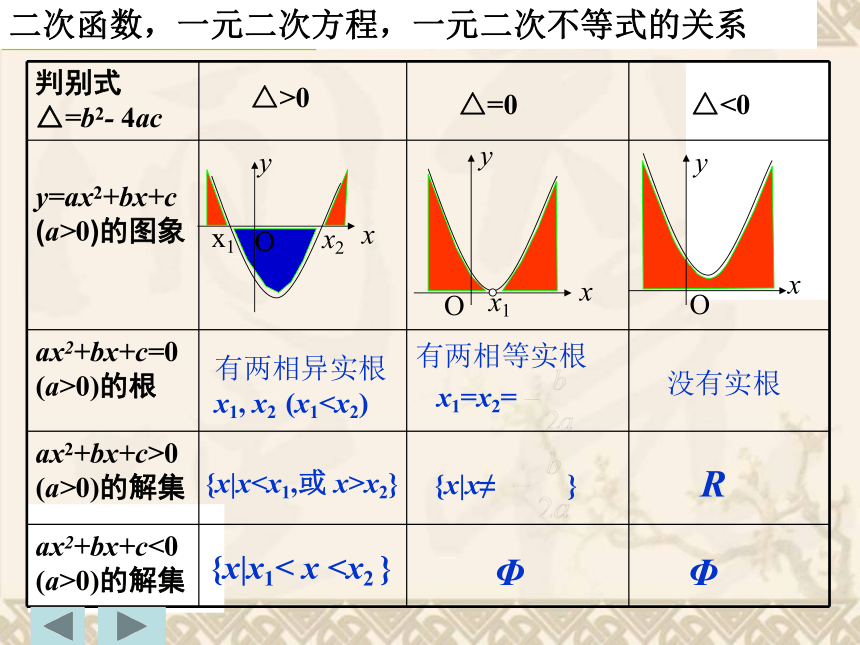
判别式
△=b2-
4ac
y=ax2+bx+c
(a>0)的图象
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
△>0
有两相异实根
x1,
x2
(x1{x|xx>x2}
{x|x1<
x
}
△=0
△<0
有两相等实根
x1=x2=
{x|x≠
}
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
一元二次不等式的解法
二次函数,一元二次方程,一元二次不等式的关系
记忆口诀:a>0(
)
大于0取两根之外,
小于0取两根中间。
大于取两边,小于取中间.
一元二次不等式的标准形式:
ax2+bx+c>0与ax2+bx+c<0(a>0)
例1.解不等式
2x2-3x-2
>
0
.
解:因为△
=(-3)2-4×2×(-2)>0,
方程的解2x2-3x-2
=0的解是
所以,原不等式的解集是
先求方程的根
然后想像图象形状
注:开口向上,大于0
解集是大于大根,小于小根(两边飞)
2
若改为:不等式
2x2-3x-2
<
0
.
注:开口向上,小于0
解集是大于小根且小于大根(两边夹)
2
解:不等式的解集为:
总结出:
解一元二次不等式ax2+bx+c>0、ax2+bx+c<0
(a>0)
(标准形)的步骤是:
(1)判定△的符号,
(2)
求出方程ax2+bx+c=0
的实根;(画出函数图像)
(3)(结合函数图象)写出不等式的解集.
(大于0解集是大于大根或小于小根,小于0解集是大于小根且小于大根)
因为△=
16
-16
=0
方程
4
x2
-
4x
+1=0
的解
x1=x2=1/2
故原不等式的解集为{
x|
x
≠
1/2
}
例3:解不等式-
x2
+
2x
–
3
>0
解:整理,得
x2
-
2x
+
3
<
0
因为△=
4
-
12
=
-
8
<
0
方程
2
x2
-
3x
–
2
=
0无实数根
所以原不等式的解集为ф
例2:解不等式4x2+1>4x
解:整理,得
4x2-4x+1>0
总结出:
解一元二次不等式
ax2+bx+c>0、ax2+bx+c<0
的步骤是:
(1)化成标准形式
ax2+bx+c>0
(a>0)
ax2+bx+c<0
(a>0)
(2)判定△的符号,
(3)
求出方程ax2+bx+c=0
的实根;(画出函数图像)
(4)(结合函数图象)写出不等式的解集.
简记为:一化—二判—三求—四写
答案:
巩固练习
0
2
6
2
0
2
7
3
1
1
2
2
?
+
-
-
<
+
-
x
x
x
x
;
)
(
;
)
(
、解下列一元二次不等式:
判别式
△=b2-
4ac
y=ax2+bx+c
(a>0)的图象
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
△>0
有两相异实根
x1,
x2
(x1{x|xx>x2}
{x|x1<
x
}
△=0
△<0
有两相等实根
x1=x2=
{x|x≠
}
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
一元二次不等式的解法
1.二次函数,一元二次方程,一元二次不等式的关系
2.解一元二次不等式
ax2+bx+c>0、ax2+bx+c<0
的步骤是:
(1)化成标准形式
ax2+bx+c>0
(a>0)
ax2+bx+c<0
(a>0)
(2)判定△的符号,
(3)
求出方程ax2+bx+c=0
的实根;(画出函数图像)
(4)(结合函数图象)写出不等式的解集.
简记为:一化—二判—三求—四写
3.2
一元二次不等式及其解法
(第一课时)
制作一个高为2m的长方体容器,底面矩形的长比宽少1m,并且长方体的容积大于12m3,问底面矩形的宽的取值范围?
新课引入
x2-x-6>0
一元二次不等式(定义)
新知讲解
那么怎样求一元二次不等式
x2-x-6>0的解集呢?
一个
2
x2-x-6>0
像
这样只含
未知数,并且未知数最高次数为
的不等式,称为一元二次不等式.
像
这样只含
未知数,并且未知数最高次数为
的不等式,称为一元二次不等式.
画出函数y=x2-x-6的图象,并根据图象回答:
(1).图象与x轴交点的坐标为
,
该坐标与方程
x2
-x-6=0的解有什么关系:
。
(2).当x取
时,y=0?
当x取
时,y>0?
当x取
时,y<0?
(3).由图象写出:
不等式x2
-x-6>0
的
解集为
。
不等式x2
-x-6<0
的
解集为
。
(-2,
0),(3,
0)
交点的横坐标即为方程的根
x=
-2
或
3
x<-2
或
x>3
-2
<
x
<3
﹛x|x<-2或x>3﹜
﹛x|
-2
y
x
0
-2
3
o
o
o
o
y>0
y>0
y<0
方程
ax2+bx+c=0、
不等式ax2+bx+c>0、
或ax2+bx+c<0
与函数y=
ax2+bx+c>0的图象有什么关系?
思考:
结论:方程的解即函数图象与x轴交点的横坐标,不等式的解集即函数图象在x轴上方或下方图象所对应x的范围。
判别式
△=b2-
4ac
y=ax2+bx+c
(a>0)的图象
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
△>0
有两相异实根
x1,
x2
(x1
{x|x1<
x
△=0
△<0
有两相等实根
x1=x2=
{x|x≠
}
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
一元二次不等式的解法
二次函数,一元二次方程,一元二次不等式的关系
记忆口诀:a>0(
)
大于0取两根之外,
小于0取两根中间。
大于取两边,小于取中间.
一元二次不等式的标准形式:
ax2+bx+c>0与ax2+bx+c<0(a>0)
例1.解不等式
2x2-3x-2
>
0
.
解:因为△
=(-3)2-4×2×(-2)>0,
方程的解2x2-3x-2
=0的解是
所以,原不等式的解集是
先求方程的根
然后想像图象形状
注:开口向上,大于0
解集是大于大根,小于小根(两边飞)
2
若改为:不等式
2x2-3x-2
<
0
.
注:开口向上,小于0
解集是大于小根且小于大根(两边夹)
2
解:不等式的解集为:
总结出:
解一元二次不等式ax2+bx+c>0、ax2+bx+c<0
(a>0)
(标准形)的步骤是:
(1)判定△的符号,
(2)
求出方程ax2+bx+c=0
的实根;(画出函数图像)
(3)(结合函数图象)写出不等式的解集.
(大于0解集是大于大根或小于小根,小于0解集是大于小根且小于大根)
因为△=
16
-16
=0
方程
4
x2
-
4x
+1=0
的解
x1=x2=1/2
故原不等式的解集为{
x|
x
≠
1/2
}
例3:解不等式-
x2
+
2x
–
3
>0
解:整理,得
x2
-
2x
+
3
<
0
因为△=
4
-
12
=
-
8
<
0
方程
2
x2
-
3x
–
2
=
0无实数根
所以原不等式的解集为ф
例2:解不等式4x2+1>4x
解:整理,得
4x2-4x+1>0
总结出:
解一元二次不等式
ax2+bx+c>0、ax2+bx+c<0
的步骤是:
(1)化成标准形式
ax2+bx+c>0
(a>0)
ax2+bx+c<0
(a>0)
(2)判定△的符号,
(3)
求出方程ax2+bx+c=0
的实根;(画出函数图像)
(4)(结合函数图象)写出不等式的解集.
简记为:一化—二判—三求—四写
答案:
巩固练习
0
2
6
2
0
2
7
3
1
1
2
2
?
+
-
-
<
+
-
x
x
x
x
;
)
(
;
)
(
、解下列一元二次不等式:
判别式
△=b2-
4ac
y=ax2+bx+c
(a>0)的图象
ax2+bx+c=0
(a>0)的根
ax2+bx+c>0
(a>0)的解集
ax2+bx+c<0
(a>0)的解集
△>0
有两相异实根
x1,
x2
(x1
{x|x1<
x
△=0
△<0
有两相等实根
x1=x2=
{x|x≠
}
x1
x2
x
y
O
y
x
O
Φ
Φ
R
没有实根
y
x
O
x1
一元二次不等式的解法
1.二次函数,一元二次方程,一元二次不等式的关系
2.解一元二次不等式
ax2+bx+c>0、ax2+bx+c<0
的步骤是:
(1)化成标准形式
ax2+bx+c>0
(a>0)
ax2+bx+c<0
(a>0)
(2)判定△的符号,
(3)
求出方程ax2+bx+c=0
的实根;(画出函数图像)
(4)(结合函数图象)写出不等式的解集.
简记为:一化—二判—三求—四写
