苏科版七年级上册课时练:第四章《一元一次方程》实际应用解答题提优(三)(Word版 含解析)
文档属性
| 名称 | 苏科版七年级上册课时练:第四章《一元一次方程》实际应用解答题提优(三)(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 33.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 21:59:12 | ||
图片预览



文档简介
课时练:第四章《一元一次方程》
实际应用解答题提优(三)
1.一次奥运知识竞赛中,一共有25道题,答对一题得10分,答错(或不答)一题扣5分.设小明同学在这次竞赛中答对x道题.
(1)根据所给条件,完成下表:
答题情况
答对
答错或不答
题数
x
每题分值
10
﹣5
得分
10x
(2)若小明同学的竞赛成绩超过100分,则他至少答对几道题?
2.京津城际铁路将于8月1日开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京的行驶时间与预计时间相同.如果这次试车时,由天津返回北京比去天津时平均每小时多行驶40千米,那么这次试车时由北京到天津的平均速度是每小时多少千米?
3.某乳制品厂,现有鲜牛奶10吨,若直接销售,每吨可获利500元;若制成酸奶销售,每吨可获利1200元;若制成奶粉销售,每吨可获利2000元,本工厂的生产能力是:若制成酸奶,每天可加工鲜牛奶3吨;若制成奶粉,每天可加工鲜牛奶1吨(两种加工方式不能同时进行).受气温条件限制,这批鲜牛奶必须在4天内全部销售或加工完成.为此该厂设计了以下两种可行方案:
方案一:4天时间全部用来生产奶粉,其余直接销售鲜奶;
方案二:将一部分制成奶粉,其余制成酸奶,并恰好4天完成.
你认为哪种方案获利最多,为什么?
4.某石油进口国这个月的石油进口量比上个月减少了5%,由于国际油价上涨,这个月进口石油的费用反而比上个月增加了14%.求这个月的石油价格相对上个月的增长率.
5.为了确保汶川灾区唐家山“堰塞湖”下游群众的安全,需开挖一条泄洪槽,经专家测算,抢险部队计划用10天时间开挖土石13.55万方,施工一天后,考虑天气等不可测因素,为保万无一失,增加了大量设备以提高开挖效率,结果提前4天完成任务.问:提高效率后,平均每天比原计划多开挖土石多少万方?
6.从甲地到乙地,某人骑自行车比乘公共汽车多用2.5h,已知骑自行车的平均速度为每小时15km,公共汽车的平均速度为每小时40km,求甲乙两地之间的路程(只列方程).
7.生态公园计划在园内的坡地上种植一片有A、B两种树的混合林,需要购买这两种树苗共100棵.假设这批树苗种植后成活95棵,种植A、B两种树苗的相关信息如下表:
品名
单价(元/棵)
栽树劳务费(元/棵)
成活率
A
15
3
96%
B
20
4
92%
(1)设购买A种树苗x棵,则购买B种树苗
棵,根据题意可列方程为
,解得x=
.
(2)求种植这片混合林的总费用需多少元?
8.李明和爸爸比身高,两人站一起时,发现自己的身高只到爸爸身高的一半.他又去搬来28cm高的小板凳,发现这时到了爸爸身高的处.问李明和爸爸的身高分别为多少?
9.重温例题:
小丽在水果店花18元买了苹果和橘子共6千克,已知苹果每千克3.2元,橘子每千克2.6元.小丽买了苹果和橘子各多少千克?
解决问题:
(1)设所购买的苹果质量为xkg.请你将下列同学的探究过程补充完整.
①小明同学列出了下表,并根据相等关系“买苹果的金额+买橘子的金额=18元”,可得方程:
.
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
3.2x
橘子
2.6
6﹣x
2.6(6﹣x)
合计
6
18
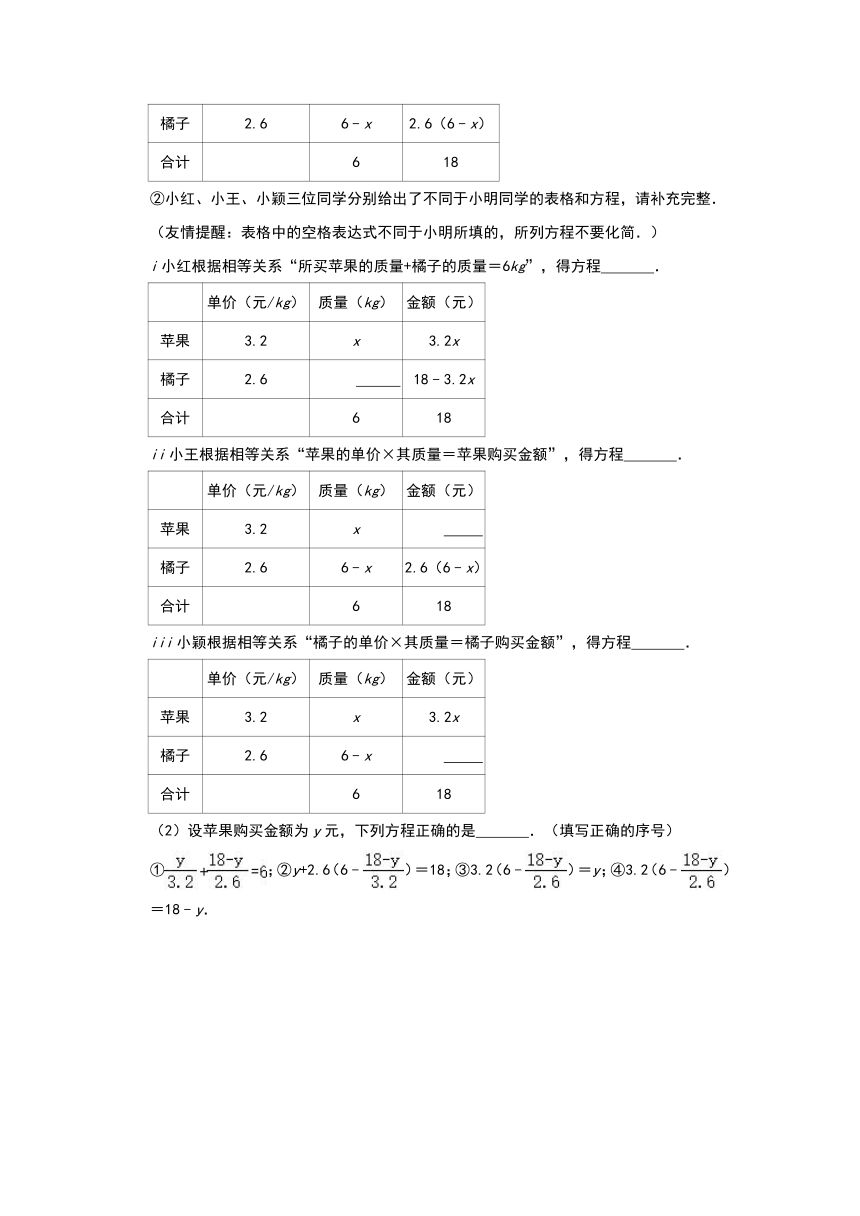
②小红、小王、小颖三位同学分别给出了不同于小明同学的表格和方程,请补充完整.
(友情提醒:表格中的空格表达式不同于小明所填的,所列方程不要化简.)
i小红根据相等关系“所买苹果的质量+橘子的质量=6kg”,得方程
.
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
3.2x
橘子
2.6
18﹣3.2x
合计
6
18
ii小王根据相等关系“苹果的单价×其质量=苹果购买金额”,得方程
.
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
橘子
2.6
6﹣x
2.6(6﹣x)
合计
6
18
iii小颖根据相等关系“橘子的单价×其质量=橘子购买金额”,得方程
.
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
3.2x
橘子
2.6
6﹣x
合计
6
18
(2)设苹果购买金额为y元,下列方程正确的是
.(填写正确的序号)
①;②y+2.6(6﹣)=18;③3.2(6﹣)=y;④3.2(6﹣)=18﹣y.
10.运动场的跑道一圈长400米,小健练习骑自行车,平均每分骑350米,小康练习跑步,平均每分跑250米.
(1)两人从同一处同时反向出发,经多长时间首次相遇?
(2)若两人从同一处同时同向出发,经过多少时间首次相遇?
参考答案
1.解:(1)补全表格:
答题情况
答对
答错或不答
题数
x
25﹣x
每题分值
10
﹣5
得分
10x
﹣5(25﹣x)
(2)根据题意,得10x﹣5(25﹣x)>100,即15x﹣125>100,
解得x>15.
∴x的最小正整数解是x=16.
答:小明同学至少答对16道题.
2.解:设这次试车时,由北京到天津的平均速度是每小时x千米,则由天津返回北京的平均速度是每小时(x+40)千米
依题意得:(x+40)
解得:x=200.
答:这次试车时,由北京到天津的平均速度是每小时200千米.
3.解:方案一:4×2000+6×500=11000(元)
方案二:设制奶粉x天,
则:1×x+(4﹣x)×3=10,
解得:x=1(天),
故:1×1×2000+3×3×1200=12800>11000,
故选方案二.
4.解:设这个月的石油价格相对上个月的增长率为x.
根据题意得:(1+x)(1﹣5%)=1+14%.
解得:x==20%.
答:这个月的石油价格相对上个月的增长率为20%.
5.解:提高效率后,平均每天比原计划多开挖土石x万方,
根据题意得:原计划每天挖运=1.355(万方),
则提高效率后每天开挖(x+1.355)万方,
∴1.355+5(x+1.355)=13.55
解得:x=1.084
答:提高效率后,平均每天比原计划多开挖土石1.084万方.
6.解:设甲乙两地之间的路程为x千米,由题意得
+2.5=.
7.解:(1)设购买A种树苗x棵,则购买B种树苗(100﹣x)棵,
依题意,得:96%x+92%(100﹣x)=95,
解得:x=75.
故答案为:(100﹣x);96%x+92%(100﹣x)=95;75.
(2)(15+3)×75+(20+4)×(100﹣75)=1950(元).
答:种植这片混合林的总费用需1950元.
8.解:设李明的身高为xcm,则爸爸的身高为2xcm,
根据题意,得x+28=?2x,
解得:x=84,
则2x=168.
答:李明的身高是84cm,爸爸的身高是168cm.
9.解:(1)①设小丽买了x千克的苹果,则她买橘子(6﹣x)千克.
由题意得:3.2x+2.6(6﹣x)=18;
故答案为:3.2x+2.6(6﹣x)=18;
②i补全表格如下:
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
3.2x
橘子
2.6
18﹣3.2x
合计
6
18
根据相等关系“所买苹果的质量+橘子的质量=6kg”,得方程:x+=6,
故答案为:x+=6;
ii补全表格如下:
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
18﹣2.6(6﹣x)
橘子
2.6
6﹣x
2.6(6﹣x)
合计
6
18
根据相等关系“苹果的单价×其质量=苹果购买金额”,得方程:3.2x=18﹣2.6(6﹣x),
故答案为:3.2x=18﹣2.6(6﹣x).
iii补全表格如下:
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
3.2x
橘子
2.6
6﹣x
18﹣3.2x
合计
6
18
根据相等关系“橘子的单价×其质量=橘子购买金额”,得方程:2.6(6﹣x)=18﹣3.2x,
故答案为:2.6(6﹣x)=18﹣3.2x.
(2)设苹果购买金额为y元,所列方程正确的是①③,
故答案为:①③.
10.解:(1)设两人从同一处同时反向出发,经x分钟时间首次相遇,
根据题意得:(350+250)x=400,
解得:x=,
则两人从同一处同时反向出发,经分钟首次相遇;
(2)设两人从同一处同时同向出发,经过y分钟首次相遇,
根据题意得:(350﹣250)y=400,
解得:y=4,
则两人从同一处同时同向出发,经过4分钟首次相遇.
实际应用解答题提优(三)
1.一次奥运知识竞赛中,一共有25道题,答对一题得10分,答错(或不答)一题扣5分.设小明同学在这次竞赛中答对x道题.
(1)根据所给条件,完成下表:
答题情况
答对
答错或不答
题数
x
每题分值
10
﹣5
得分
10x
(2)若小明同学的竞赛成绩超过100分,则他至少答对几道题?
2.京津城际铁路将于8月1日开通运营,预计高速列车在北京、天津间单程直达运行时间为半小时.某次试车时,试验列车由北京到天津的行驶时间比预计时间多用了6分钟,由天津返回北京的行驶时间与预计时间相同.如果这次试车时,由天津返回北京比去天津时平均每小时多行驶40千米,那么这次试车时由北京到天津的平均速度是每小时多少千米?
3.某乳制品厂,现有鲜牛奶10吨,若直接销售,每吨可获利500元;若制成酸奶销售,每吨可获利1200元;若制成奶粉销售,每吨可获利2000元,本工厂的生产能力是:若制成酸奶,每天可加工鲜牛奶3吨;若制成奶粉,每天可加工鲜牛奶1吨(两种加工方式不能同时进行).受气温条件限制,这批鲜牛奶必须在4天内全部销售或加工完成.为此该厂设计了以下两种可行方案:
方案一:4天时间全部用来生产奶粉,其余直接销售鲜奶;
方案二:将一部分制成奶粉,其余制成酸奶,并恰好4天完成.
你认为哪种方案获利最多,为什么?
4.某石油进口国这个月的石油进口量比上个月减少了5%,由于国际油价上涨,这个月进口石油的费用反而比上个月增加了14%.求这个月的石油价格相对上个月的增长率.
5.为了确保汶川灾区唐家山“堰塞湖”下游群众的安全,需开挖一条泄洪槽,经专家测算,抢险部队计划用10天时间开挖土石13.55万方,施工一天后,考虑天气等不可测因素,为保万无一失,增加了大量设备以提高开挖效率,结果提前4天完成任务.问:提高效率后,平均每天比原计划多开挖土石多少万方?
6.从甲地到乙地,某人骑自行车比乘公共汽车多用2.5h,已知骑自行车的平均速度为每小时15km,公共汽车的平均速度为每小时40km,求甲乙两地之间的路程(只列方程).
7.生态公园计划在园内的坡地上种植一片有A、B两种树的混合林,需要购买这两种树苗共100棵.假设这批树苗种植后成活95棵,种植A、B两种树苗的相关信息如下表:
品名
单价(元/棵)
栽树劳务费(元/棵)
成活率
A
15
3
96%
B
20
4
92%
(1)设购买A种树苗x棵,则购买B种树苗
棵,根据题意可列方程为
,解得x=
.
(2)求种植这片混合林的总费用需多少元?
8.李明和爸爸比身高,两人站一起时,发现自己的身高只到爸爸身高的一半.他又去搬来28cm高的小板凳,发现这时到了爸爸身高的处.问李明和爸爸的身高分别为多少?
9.重温例题:
小丽在水果店花18元买了苹果和橘子共6千克,已知苹果每千克3.2元,橘子每千克2.6元.小丽买了苹果和橘子各多少千克?
解决问题:
(1)设所购买的苹果质量为xkg.请你将下列同学的探究过程补充完整.
①小明同学列出了下表,并根据相等关系“买苹果的金额+买橘子的金额=18元”,可得方程:
.
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
3.2x
橘子
2.6
6﹣x
2.6(6﹣x)
合计
6
18
②小红、小王、小颖三位同学分别给出了不同于小明同学的表格和方程,请补充完整.
(友情提醒:表格中的空格表达式不同于小明所填的,所列方程不要化简.)
i小红根据相等关系“所买苹果的质量+橘子的质量=6kg”,得方程
.
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
3.2x
橘子
2.6
18﹣3.2x
合计
6
18
ii小王根据相等关系“苹果的单价×其质量=苹果购买金额”,得方程
.
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
橘子
2.6
6﹣x
2.6(6﹣x)
合计
6
18
iii小颖根据相等关系“橘子的单价×其质量=橘子购买金额”,得方程
.
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
3.2x
橘子
2.6
6﹣x
合计
6
18
(2)设苹果购买金额为y元,下列方程正确的是
.(填写正确的序号)
①;②y+2.6(6﹣)=18;③3.2(6﹣)=y;④3.2(6﹣)=18﹣y.
10.运动场的跑道一圈长400米,小健练习骑自行车,平均每分骑350米,小康练习跑步,平均每分跑250米.
(1)两人从同一处同时反向出发,经多长时间首次相遇?
(2)若两人从同一处同时同向出发,经过多少时间首次相遇?
参考答案
1.解:(1)补全表格:
答题情况
答对
答错或不答
题数
x
25﹣x
每题分值
10
﹣5
得分
10x
﹣5(25﹣x)
(2)根据题意,得10x﹣5(25﹣x)>100,即15x﹣125>100,
解得x>15.
∴x的最小正整数解是x=16.
答:小明同学至少答对16道题.
2.解:设这次试车时,由北京到天津的平均速度是每小时x千米,则由天津返回北京的平均速度是每小时(x+40)千米
依题意得:(x+40)
解得:x=200.
答:这次试车时,由北京到天津的平均速度是每小时200千米.
3.解:方案一:4×2000+6×500=11000(元)
方案二:设制奶粉x天,
则:1×x+(4﹣x)×3=10,
解得:x=1(天),
故:1×1×2000+3×3×1200=12800>11000,
故选方案二.
4.解:设这个月的石油价格相对上个月的增长率为x.
根据题意得:(1+x)(1﹣5%)=1+14%.
解得:x==20%.
答:这个月的石油价格相对上个月的增长率为20%.
5.解:提高效率后,平均每天比原计划多开挖土石x万方,
根据题意得:原计划每天挖运=1.355(万方),
则提高效率后每天开挖(x+1.355)万方,
∴1.355+5(x+1.355)=13.55
解得:x=1.084
答:提高效率后,平均每天比原计划多开挖土石1.084万方.
6.解:设甲乙两地之间的路程为x千米,由题意得
+2.5=.
7.解:(1)设购买A种树苗x棵,则购买B种树苗(100﹣x)棵,
依题意,得:96%x+92%(100﹣x)=95,
解得:x=75.
故答案为:(100﹣x);96%x+92%(100﹣x)=95;75.
(2)(15+3)×75+(20+4)×(100﹣75)=1950(元).
答:种植这片混合林的总费用需1950元.
8.解:设李明的身高为xcm,则爸爸的身高为2xcm,
根据题意,得x+28=?2x,
解得:x=84,
则2x=168.
答:李明的身高是84cm,爸爸的身高是168cm.
9.解:(1)①设小丽买了x千克的苹果,则她买橘子(6﹣x)千克.
由题意得:3.2x+2.6(6﹣x)=18;
故答案为:3.2x+2.6(6﹣x)=18;
②i补全表格如下:
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
3.2x
橘子
2.6
18﹣3.2x
合计
6
18
根据相等关系“所买苹果的质量+橘子的质量=6kg”,得方程:x+=6,
故答案为:x+=6;
ii补全表格如下:
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
18﹣2.6(6﹣x)
橘子
2.6
6﹣x
2.6(6﹣x)
合计
6
18
根据相等关系“苹果的单价×其质量=苹果购买金额”,得方程:3.2x=18﹣2.6(6﹣x),
故答案为:3.2x=18﹣2.6(6﹣x).
iii补全表格如下:
单价(元/kg)
质量(kg)
金额(元)
苹果
3.2
x
3.2x
橘子
2.6
6﹣x
18﹣3.2x
合计
6
18
根据相等关系“橘子的单价×其质量=橘子购买金额”,得方程:2.6(6﹣x)=18﹣3.2x,
故答案为:2.6(6﹣x)=18﹣3.2x.
(2)设苹果购买金额为y元,所列方程正确的是①③,
故答案为:①③.
10.解:(1)设两人从同一处同时反向出发,经x分钟时间首次相遇,
根据题意得:(350+250)x=400,
解得:x=,
则两人从同一处同时反向出发,经分钟首次相遇;
(2)设两人从同一处同时同向出发,经过y分钟首次相遇,
根据题意得:(350﹣250)y=400,
解得:y=4,
则两人从同一处同时同向出发,经过4分钟首次相遇.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
