人教版八年级上册数学14.3因式分解 十字相乘法 课件(19张)
文档属性
| 名称 | 人教版八年级上册数学14.3因式分解 十字相乘法 课件(19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 662.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览






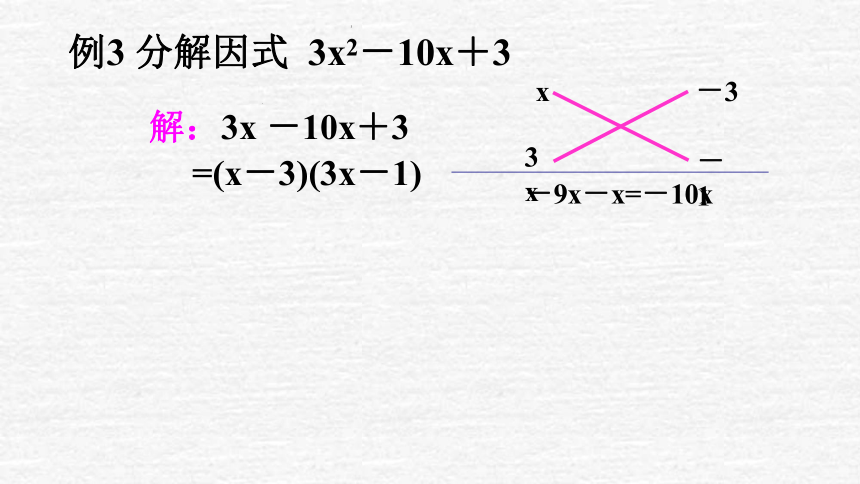
文档简介
十字相乘法:
对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
x2+(p+q)x+pq=(x+p)(x+q)
简记口诀:
首尾分解,交叉相乘,
求和凑中,横写因式。
十字相乘法:
对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
x
x
p
q
px+qx=(p+q)x
x
2
pq
x2+(p+q)x+pq=(x+p)(x+q)
例1 分解因式 x2-6x+8
2
解:x -6x+8
2
x
x
-2
-4
-4x-2x=-6x
=(x-2)(x-4)
简记口诀:首尾分解,交叉相乘,求和凑中,横写因式。
练一练:
小结:
将下列各式分解因式
当常数项为正数时,拆分成的两个有理数一定同号,符号与一次项系数相同;
当常数项为负数时,拆分成的两个有理数异号,绝对值大的数与一次项系数同号
练一练:
将下列各式分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
例2 分解因式:
解:
例3 分解因式 3x2-10x+3
2
解:3x -10x+3
2
x
3x
-3
-1
-9x-x=-10x
=(x-3)(3x-1)
(1)2x2 + 13x + 15
(2)3x2 - 15x - 18
( 3 ) -6x2 +3x +18
( 4 ) 2x2+5xy - 12y2
( 5 ) 6x2 - 7xy – 5y2
(6)(x+y)2 + 4(x+y) - 5
(7) 2(a+b)2 + 3(a+b) – 2
(8) 2(6x2 +x) 2-11(6x2 +x) +5
分组分解法
要发现式中隐含的条件,通过交换项的位置,添、去括号等一些变换达到因式分解的目的。
例1:因式分解 ab–ac+bd–cd
解:原式 = (ab – ac) + (bd – cd)
= a (b – c) + d (b – c)
= (a + d) (b – c)
还有别的解法吗?
分组分解法
要发现式中隐含的条件,通过交换项的位置,添、去括号等一些变换达到因式分解的目的。
例1:因式分解 ab–ac+bd–cd
解:原式 = (ab + bd) – (ac + cd)
= b (a + d) – c (a + d)
= (a + d) (b – c)
例2:因式分解 x5+x4+x3+x2+x+1 。
解:原式 = (x5+x4+x3)+(x2+x+1)
= (x3+1)(x2+x+1)
= (x+1)(x2–x+1)(x2+x+1)
立方和公式
分组分解法随堂练习:
1)xy–xz–y2+2yz–z2
2)a2–b2–c2–2bc–2a+1
配方法
配方法是一种特殊的拆项添项法,将多项式配成完全平方式,再用平方差公式进行分解。
因式分解 a2–b2+4a+2b+3
解:原式 = (a2+4a+4) – (b2–2b+1)
= (a+2)2 – (b–1)2
= (a+b+1)(a–b+3)
回顾例题:因式分解 x5+x4+x3+x2+x+1 。
另解:原式 = (x5+x4)+(x3+x2)+(x+1)
= (x+1)(x4+x2+1)
= (x+1)(x4+2x2+1–x2)
= (x+1)[(x2+1)2–x2]
= (x+1)(x2+x+1)(x2–x+1)
拆项添项法
怎么结果与刚才不一样呢?
因为它还可以继续因式分解
因式分解 x4 + 4
解:原式 = x4 + 4x2 + 4 – 4x2
= (x2+2)2 – (2x)2
= (x2+2x+2)(x2–2x+2)
都是平方项
猜测使用完全平方公式
完全平方公式
平方差公式
拆项添项法随堂练习:
1)x4–23x2y2+y4
2)(m2–1)(n2–1)+4mn
= 3
= 14
10
+ 4
2 x2 + 3 xy – 9 y2 + 14 x – 3 y + 20
双十字相乘法
双十字相乘法适用于二次六项式的因式分解,而待定系数法则没有这个限制。
因式分解 2x2+3xy–9y2+14x–3y+20
2
1
–3
3
6
– 3
4
5
= –3
12
– 15
∴原式 = (2x–3y+4)(x+3y+5)
1
2
-5
-1
-1-10=-11
练习1 将 2(6x +x) -11(6x +x) +5 分解因式
2
2
2
解:2(6x +x)-11(6x +x) +5
2
2
2
= [(6x +x) -5][2(6x +x)-1]
2
2
= (6x +x-5) (12x +2x-1 )
2
2
= (6x -5)(x +1) (12x +2x-1 )
2
6
1
-5
1
-5+6=1
练习2 将 2x -3xy-2y +3x+4y-2 分解因式
2
2
解: 2x -3xy-2y +3x+4y-2
2
2
=(2x -3xy-2y )+3x+4y-2
2
2
=(2x +y)(x-2y)+3x+4y-2
=(2x +y-1)(x-2y+2)
2
1
1
-2
-4+1=-3
(2x+y)
(x-2y)
-1
2
2(2x+y) - (x- 2 y)=3x+4y
待定系数法
因式分解 2x2+3xy–9y2+14x–3y+20。
通过十字相乘法得到 (2x–3y)(x+3y)
设原式等于(2x–3y+a)(x+3y+b)
通过比较两式同类项的系数可得:
解得: ,∴原式 = (2x–3y+4)(x+3y+5)
对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
x2+(p+q)x+pq=(x+p)(x+q)
简记口诀:
首尾分解,交叉相乘,
求和凑中,横写因式。
十字相乘法:
对于二次三项式的分解因式,借用一个十字叉帮助我们分解因式,这种方法叫做十字相乘法。
x
x
p
q
px+qx=(p+q)x
x
2
pq
x2+(p+q)x+pq=(x+p)(x+q)
例1 分解因式 x2-6x+8
2
解:x -6x+8
2
x
x
-2
-4
-4x-2x=-6x
=(x-2)(x-4)
简记口诀:首尾分解,交叉相乘,求和凑中,横写因式。
练一练:
小结:
将下列各式分解因式
当常数项为正数时,拆分成的两个有理数一定同号,符号与一次项系数相同;
当常数项为负数时,拆分成的两个有理数异号,绝对值大的数与一次项系数同号
练一练:
将下列各式分解因式
提示:当二次项系数为-1时 ,先提出负号再因式分解 。
例2 分解因式:
解:
例3 分解因式 3x2-10x+3
2
解:3x -10x+3
2
x
3x
-3
-1
-9x-x=-10x
=(x-3)(3x-1)
(1)2x2 + 13x + 15
(2)3x2 - 15x - 18
( 3 ) -6x2 +3x +18
( 4 ) 2x2+5xy - 12y2
( 5 ) 6x2 - 7xy – 5y2
(6)(x+y)2 + 4(x+y) - 5
(7) 2(a+b)2 + 3(a+b) – 2
(8) 2(6x2 +x) 2-11(6x2 +x) +5
分组分解法
要发现式中隐含的条件,通过交换项的位置,添、去括号等一些变换达到因式分解的目的。
例1:因式分解 ab–ac+bd–cd
解:原式 = (ab – ac) + (bd – cd)
= a (b – c) + d (b – c)
= (a + d) (b – c)
还有别的解法吗?
分组分解法
要发现式中隐含的条件,通过交换项的位置,添、去括号等一些变换达到因式分解的目的。
例1:因式分解 ab–ac+bd–cd
解:原式 = (ab + bd) – (ac + cd)
= b (a + d) – c (a + d)
= (a + d) (b – c)
例2:因式分解 x5+x4+x3+x2+x+1 。
解:原式 = (x5+x4+x3)+(x2+x+1)
= (x3+1)(x2+x+1)
= (x+1)(x2–x+1)(x2+x+1)
立方和公式
分组分解法随堂练习:
1)xy–xz–y2+2yz–z2
2)a2–b2–c2–2bc–2a+1
配方法
配方法是一种特殊的拆项添项法,将多项式配成完全平方式,再用平方差公式进行分解。
因式分解 a2–b2+4a+2b+3
解:原式 = (a2+4a+4) – (b2–2b+1)
= (a+2)2 – (b–1)2
= (a+b+1)(a–b+3)
回顾例题:因式分解 x5+x4+x3+x2+x+1 。
另解:原式 = (x5+x4)+(x3+x2)+(x+1)
= (x+1)(x4+x2+1)
= (x+1)(x4+2x2+1–x2)
= (x+1)[(x2+1)2–x2]
= (x+1)(x2+x+1)(x2–x+1)
拆项添项法
怎么结果与刚才不一样呢?
因为它还可以继续因式分解
因式分解 x4 + 4
解:原式 = x4 + 4x2 + 4 – 4x2
= (x2+2)2 – (2x)2
= (x2+2x+2)(x2–2x+2)
都是平方项
猜测使用完全平方公式
完全平方公式
平方差公式
拆项添项法随堂练习:
1)x4–23x2y2+y4
2)(m2–1)(n2–1)+4mn
= 3
= 14
10
+ 4
2 x2 + 3 xy – 9 y2 + 14 x – 3 y + 20
双十字相乘法
双十字相乘法适用于二次六项式的因式分解,而待定系数法则没有这个限制。
因式分解 2x2+3xy–9y2+14x–3y+20
2
1
–3
3
6
– 3
4
5
= –3
12
– 15
∴原式 = (2x–3y+4)(x+3y+5)
1
2
-5
-1
-1-10=-11
练习1 将 2(6x +x) -11(6x +x) +5 分解因式
2
2
2
解:2(6x +x)-11(6x +x) +5
2
2
2
= [(6x +x) -5][2(6x +x)-1]
2
2
= (6x +x-5) (12x +2x-1 )
2
2
= (6x -5)(x +1) (12x +2x-1 )
2
6
1
-5
1
-5+6=1
练习2 将 2x -3xy-2y +3x+4y-2 分解因式
2
2
解: 2x -3xy-2y +3x+4y-2
2
2
=(2x -3xy-2y )+3x+4y-2
2
2
=(2x +y)(x-2y)+3x+4y-2
=(2x +y-1)(x-2y+2)
2
1
1
-2
-4+1=-3
(2x+y)
(x-2y)
-1
2
2(2x+y) - (x- 2 y)=3x+4y
待定系数法
因式分解 2x2+3xy–9y2+14x–3y+20。
通过十字相乘法得到 (2x–3y)(x+3y)
设原式等于(2x–3y+a)(x+3y+b)
通过比较两式同类项的系数可得:
解得: ,∴原式 = (2x–3y+4)(x+3y+5)
