人教版八年级上册数学课件:14.2.1平方差公式(21张)
文档属性
| 名称 | 人教版八年级上册数学课件:14.2.1平方差公式(21张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览








文档简介
每天告诉自己一次:
“我真的很不错”。
情境导入
王剑同学去商店买了单价是9.8元/千克的糖块10.2千克,售货员刚拿起计算器,王剑就说出应付99.96元,结果与售货员计算出的结果相吻合。售货员惊讶地问:“这位同学,你怎么算得这么快?”王剑同学说:“我利用了在数学上刚学过的一个公式。”你知道王剑同学用的是一个什么样的公式吗?
1、 会推导平方差公式,并能用公式进行简单的运算。
2、理解掌握平方差公式的结构特征,并能灵活熟练的运用平方差公式。
学习目标
问题1(算一算)计算下列多项式的积。
问题2(猜一猜)不计算,你来猜一下下面的式子的结果。
问题3(说一说)从上面的运算中你发现什么规律?
自学指导
x?-1
m?-4
x?-25y?
x?-36
a?-4
x?-y?
a?-b?
①(x + 4)( x-4)
②(1 + a)( 1-a)
③(m+ n)( m-n)
自学检测
练习:用你发现的规律
口答下列多项式的积:
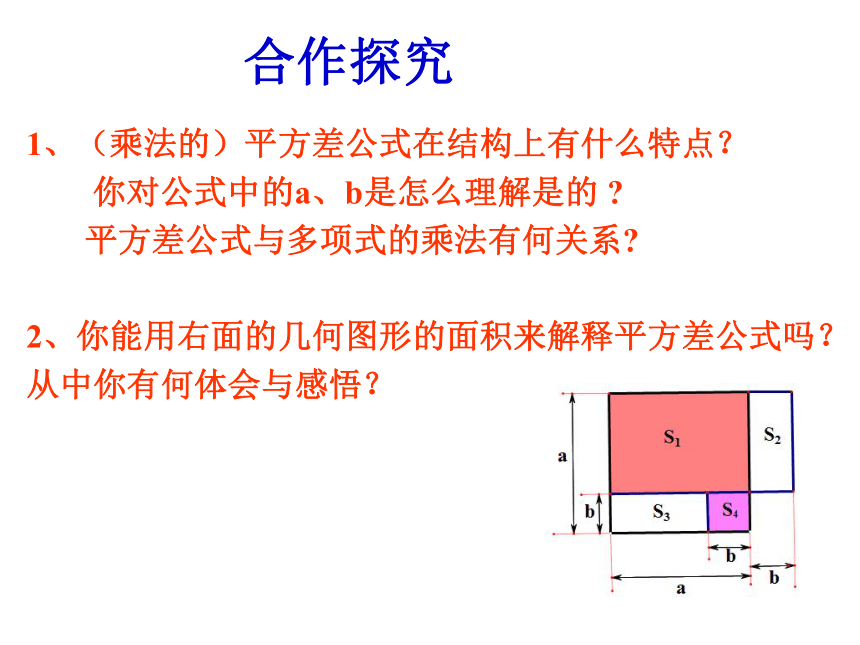
合作探究
1、(乘法的)平方差公式在结构上有什么特点?
你对公式中的a、b是怎么理解是的 ?
平方差公式与多项式的乘法有何关系?
2、你能用右面的几何图形的面积来解释平方差公式吗?
从中你有何体会与感悟?
(a+b)(a-b)
两数和与这两数差的积,等于这两数的平方差
平方差公式
特点:
☆具有完全相同的两项
☆具有互为相反数的两项
(a+b)(a-b)
(a+b)(a-b)
(a+b)(a-b)=a2-b2
公式变形:
1、(a – b ) ( a + b) = a2 - b2
2、(b + a )( -b + a ) = a2 - b2
1、公式中的a和b,既可以是具体的数,也可以是单项式或者多项式;
2、左边是两个二项式的积,并且有一项完全相同,另一项互为相反数;
3、右边是相同项的平方减去相反项的绝对值的平方。
(a+b)(a- b)=
a2- b2.
温馨提示
几何验证:
a-b
例 1: 运用平方差公式计算:
(1) (3x+2) (3x-2);
分析:在(1)中,可以把3x看成a,2看成b,即
(a + b) (a - b) = a2 - b2
(3x+2) (3x - 2) = (3x)2 - 22
解:(1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.
(2)(-x+2y)(-x-2y)
= (-x)2-(2y)2
=x2-4y2.
(2) (-x+2y) (-x-2y).
尝试练习:
1、做一做
(1)(2a+3b)(2a-3b) (2) (-2x2-y)(-2x2+y)
解:原式=(2a)2-(3b)2
=4a2-9b2
解:原式=(-2x2)2-y2
=4x4-y2
2、挑战自我
(1) (3+2a)(-3+2a) (2) (-3-5m)(5m-3)
解:原式=(2a+3)(2a-3)
=(2a)2-32
=4a2-9
解:原式=(-3-5m)(-3+5m)
=(-3)2-(5m)2
=9-25m2
点拨:
1、要认清完全相同和相反的两项
2、要对整体进行平方。
例 2: 计算
(1) 102×98 (2) (y+2) (y-2) – (y-1) (y+5)
解: (1) 102×98
=(100+2)(100-2)
= 1002-22
=10 000 – 4
= 9 996.
(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
(a+b)(a-b)= a 2- b 2
相反为b
小结
相同为a
适当交换
合理加括号
平方差公式
( )
( )
1、下列计算对不对?如果不对,怎样改正?
2)
错
1)
分析:最后结果应是两项的平方差
错
3)
分析:应先观察是哪两个数的和与这两个数的差
错
分析:应将 当作一个整体,用括号括起来再平方
达标检测
(不能)
(能)
(能)
(不能)
2、下列各式能否用平方差公式进行计算?
⑴
⑵
⑶
⑷
=a10-b4.
解:原式=(a5 )2-(b2)2
解:原式=(5+0.1)(5-0.1)
=52-(0.1)2
=25-0.01
=24.99
解:原式=(9x2-16)
-(6x2+5x -6)
=3x2-5x- 10
(1)5.1×4.9
(3)(3x+4)(3x-4)-(2x+3)(3x-2)
(2)(a5-b2)(a5+b2)
相信自己 我能行!
3、计算
4、完成下列填空
1、 ( ) ( ) =4x2-9y2
2、(5+a)( ) =25-a?
a? - b? =(a+b)(a-b)
公式逆用
( )
5、化简
(x4+y4 )
(x4+y4 )
(x4+y4)
拓展提升
变式练习
6.计算 20042 - 2003×2005;
解:
20042 - 2003×2005
= 20042 - (2004-1)(2004+1)
= 20042
- (20042-12 )
= 20042
- 20042+12
=1
拓展提升
P112习题14.2:第1题
课堂作业
“我真的很不错”。
情境导入
王剑同学去商店买了单价是9.8元/千克的糖块10.2千克,售货员刚拿起计算器,王剑就说出应付99.96元,结果与售货员计算出的结果相吻合。售货员惊讶地问:“这位同学,你怎么算得这么快?”王剑同学说:“我利用了在数学上刚学过的一个公式。”你知道王剑同学用的是一个什么样的公式吗?
1、 会推导平方差公式,并能用公式进行简单的运算。
2、理解掌握平方差公式的结构特征,并能灵活熟练的运用平方差公式。
学习目标
问题1(算一算)计算下列多项式的积。
问题2(猜一猜)不计算,你来猜一下下面的式子的结果。
问题3(说一说)从上面的运算中你发现什么规律?
自学指导
x?-1
m?-4
x?-25y?
x?-36
a?-4
x?-y?
a?-b?
①(x + 4)( x-4)
②(1 + a)( 1-a)
③(m+ n)( m-n)
自学检测
练习:用你发现的规律
口答下列多项式的积:
合作探究
1、(乘法的)平方差公式在结构上有什么特点?
你对公式中的a、b是怎么理解是的 ?
平方差公式与多项式的乘法有何关系?
2、你能用右面的几何图形的面积来解释平方差公式吗?
从中你有何体会与感悟?
(a+b)(a-b)
两数和与这两数差的积,等于这两数的平方差
平方差公式
特点:
☆具有完全相同的两项
☆具有互为相反数的两项
(a+b)(a-b)
(a+b)(a-b)
(a+b)(a-b)=a2-b2
公式变形:
1、(a – b ) ( a + b) = a2 - b2
2、(b + a )( -b + a ) = a2 - b2
1、公式中的a和b,既可以是具体的数,也可以是单项式或者多项式;
2、左边是两个二项式的积,并且有一项完全相同,另一项互为相反数;
3、右边是相同项的平方减去相反项的绝对值的平方。
(a+b)(a- b)=
a2- b2.
温馨提示
几何验证:
a-b
例 1: 运用平方差公式计算:
(1) (3x+2) (3x-2);
分析:在(1)中,可以把3x看成a,2看成b,即
(a + b) (a - b) = a2 - b2
(3x+2) (3x - 2) = (3x)2 - 22
解:(1) (3x+2)(3x-2)
=(3x)2-22
=9x2-4.
(2)(-x+2y)(-x-2y)
= (-x)2-(2y)2
=x2-4y2.
(2) (-x+2y) (-x-2y).
尝试练习:
1、做一做
(1)(2a+3b)(2a-3b) (2) (-2x2-y)(-2x2+y)
解:原式=(2a)2-(3b)2
=4a2-9b2
解:原式=(-2x2)2-y2
=4x4-y2
2、挑战自我
(1) (3+2a)(-3+2a) (2) (-3-5m)(5m-3)
解:原式=(2a+3)(2a-3)
=(2a)2-32
=4a2-9
解:原式=(-3-5m)(-3+5m)
=(-3)2-(5m)2
=9-25m2
点拨:
1、要认清完全相同和相反的两项
2、要对整体进行平方。
例 2: 计算
(1) 102×98 (2) (y+2) (y-2) – (y-1) (y+5)
解: (1) 102×98
=(100+2)(100-2)
= 1002-22
=10 000 – 4
= 9 996.
(y+2)(y-2)- (y-1)(y+5)
= y2-22-(y2+4y-5)
= y2-4-y2-4y+5
= - 4y + 1.
(a+b)(a-b)= a 2- b 2
相反为b
小结
相同为a
适当交换
合理加括号
平方差公式
( )
( )
1、下列计算对不对?如果不对,怎样改正?
2)
错
1)
分析:最后结果应是两项的平方差
错
3)
分析:应先观察是哪两个数的和与这两个数的差
错
分析:应将 当作一个整体,用括号括起来再平方
达标检测
(不能)
(能)
(能)
(不能)
2、下列各式能否用平方差公式进行计算?
⑴
⑵
⑶
⑷
=a10-b4.
解:原式=(a5 )2-(b2)2
解:原式=(5+0.1)(5-0.1)
=52-(0.1)2
=25-0.01
=24.99
解:原式=(9x2-16)
-(6x2+5x -6)
=3x2-5x- 10
(1)5.1×4.9
(3)(3x+4)(3x-4)-(2x+3)(3x-2)
(2)(a5-b2)(a5+b2)
相信自己 我能行!
3、计算
4、完成下列填空
1、 ( ) ( ) =4x2-9y2
2、(5+a)( ) =25-a?
a? - b? =(a+b)(a-b)
公式逆用
( )
5、化简
(x4+y4 )
(x4+y4 )
(x4+y4)
拓展提升
变式练习
6.计算 20042 - 2003×2005;
解:
20042 - 2003×2005
= 20042 - (2004-1)(2004+1)
= 20042
- (20042-12 )
= 20042
- 20042+12
=1
拓展提升
P112习题14.2:第1题
课堂作业
