人教版八年级数学12.2.4斜边直角边(HL)判定定理(17张)
文档属性
| 名称 | 人教版八年级数学12.2.4斜边直角边(HL)判定定理(17张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览




文档简介
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
预习目标:课本41---42
1.对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了。
2.你能画一个Rt△A'B'C' 和Rt△ABC全等吗?通过你的画图反应了什么规律?
3.斜边、直角边公理的内容是什么?你会运用吗?
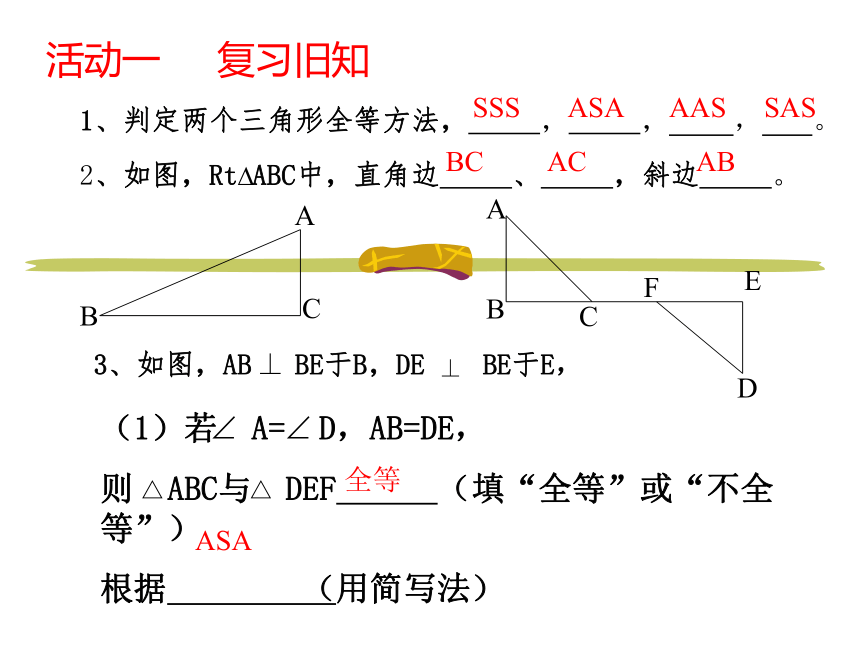
1、判定两个三角形全等方法, , , , 。
SSS
ASA
AAS
SAS
3、如图,AB BE于B,DE BE于E,
⊥
⊥
2、如图,Rt ABC中,直角边 、 ,斜边 。
A
B
C
BC
AC
AB
(1)若 A= D,AB=DE,
则 ABC与 DEF (填“全等”或“不全等”)
根据 (用简写法)
△
△
A
B
C
D
E
F
全等
ASA
活动一 复习旧知
A
B
C
D
E
F
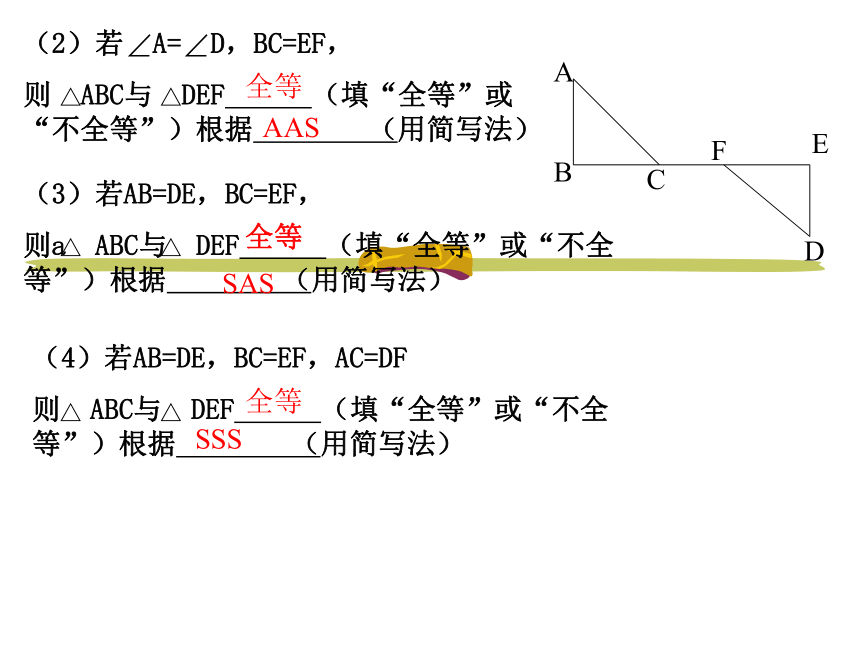
(2)若 A= D,BC=EF,
则 ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)
△
△
AAS
全等
(3)若AB=DE,BC=EF,
则a ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)
△
△
全等
SAS
(4)若AB=DE,BC=EF,AC=DF
则 ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)
△
△
全等
SSS
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
活动二 创设情景 引入新课
⑵ 如果他只带了一个卷尺,能完成这个任务吗?
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗?
(1)你能帮他想个办法吗?
方法一:测量斜边和一个对应的锐角. (AAS)
方法二:测量没遮住的一条直角边和一个对应的锐角. (ASA)或(AAS)
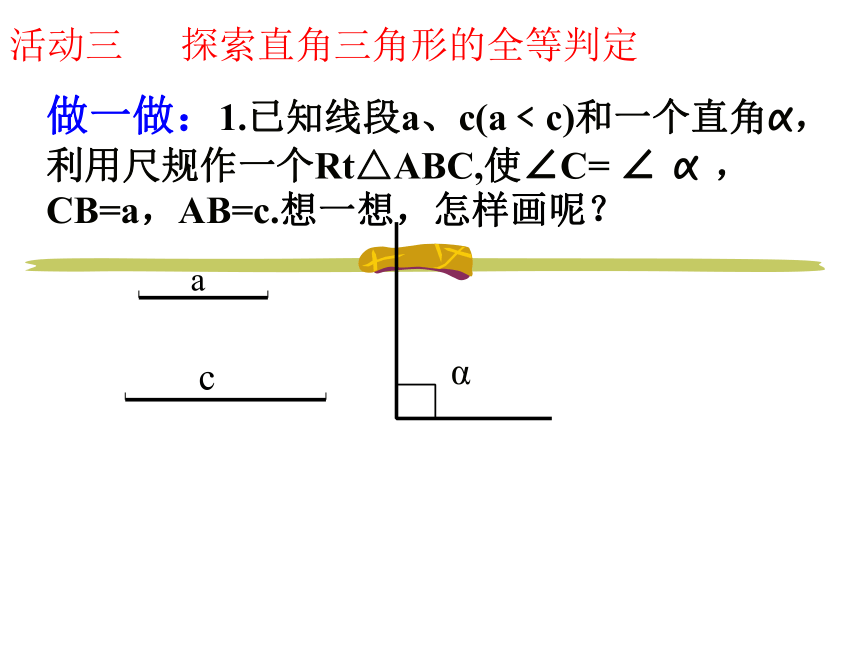
做一做:1.已知线段a、c(a﹤c)和一个直角α,利用尺规作一个Rt△ABC,使∠C= ∠ α ,CB=a,AB=c.想一想,怎样画呢?
a
c
α
活动三 探索直角三角形的全等判定
步骤如下
⑴ 作∠MCN=∠α=90°;
C
M
N
⑵ 在射线CM上截取线段CB=a;
C
M
N
B
⑶ 以点B为圆心,C为半径画弧,交射线CN于点A;
C
M
N
B
A
⑷ 连接AB.
C
M
N
B
A
⑴ △ABC就是所求作的三角形吗?
⑵ 剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?
Rt△ABC≌
A
B
C
∟
A'
B'
C'
c
a
∟
a
c
斜边、直角边公理
斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
斜边、直角边公理 (HL)
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ 中
AB=
BC=
∴Rt△ABC≌
∵∠C=∠C′=90°
斜边和一条直角边对应相等的两个直角三角形全等.
想一想 议一议
你能够用几种方法说明两个直角三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.
活动四
例题1:如图:AC⊥BC,BD⊥AD,AC=BD.求证:BC=AD.
A
B
C
D
O
在Rt△ACB和Rt△BDA中,则
AB=BA(共公边)
AC=BD.(已知)
∴ Rt△ACB≌Rt△BDA (HL).
∴BC=AD
(全等三角形对应边相等).
证明:∵ AC⊥BC,BD⊥AD
∴ ∠D=∠C=90°
练一练
2.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF.
C
D
F
E
A
B
1. 如图,AC=AD,∠C,∠D是直角,求证: BC=BD
C
D
A
B
活动五 课堂测试
C
D
A
B
C
D
A
B
A
B
C
E
D
小结
直角三角形 全等的条件:
1)定义法;
SSS;
SAS;
ASA;
AAS.
2)解题中常用的4种方法
3)HL
直角三角形全等用
一般不用
这节课你有什么收获呢?
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
直角三角形全等的判定
预习目标:课本41---42
1.对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了。
2.你能画一个Rt△A'B'C' 和Rt△ABC全等吗?通过你的画图反应了什么规律?
3.斜边、直角边公理的内容是什么?你会运用吗?
1、判定两个三角形全等方法, , , , 。
SSS
ASA
AAS
SAS
3、如图,AB BE于B,DE BE于E,
⊥
⊥
2、如图,Rt ABC中,直角边 、 ,斜边 。
A
B
C
BC
AC
AB
(1)若 A= D,AB=DE,
则 ABC与 DEF (填“全等”或“不全等”)
根据 (用简写法)
△
△
A
B
C
D
E
F
全等
ASA
活动一 复习旧知
A
B
C
D
E
F
(2)若 A= D,BC=EF,
则 ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)
△
△
AAS
全等
(3)若AB=DE,BC=EF,
则a ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)
△
△
全等
SAS
(4)若AB=DE,BC=EF,AC=DF
则 ABC与 DEF (填“全等”或“不全等”)根据 (用简写法)
△
△
全等
SSS
如图,舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.
活动二 创设情景 引入新课
⑵ 如果他只带了一个卷尺,能完成这个任务吗?
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”.你相信他的结论吗?
(1)你能帮他想个办法吗?
方法一:测量斜边和一个对应的锐角. (AAS)
方法二:测量没遮住的一条直角边和一个对应的锐角. (ASA)或(AAS)
做一做:1.已知线段a、c(a﹤c)和一个直角α,利用尺规作一个Rt△ABC,使∠C= ∠ α ,CB=a,AB=c.想一想,怎样画呢?
a
c
α
活动三 探索直角三角形的全等判定
步骤如下
⑴ 作∠MCN=∠α=90°;
C
M
N
⑵ 在射线CM上截取线段CB=a;
C
M
N
B
⑶ 以点B为圆心,C为半径画弧,交射线CN于点A;
C
M
N
B
A
⑷ 连接AB.
C
M
N
B
A
⑴ △ABC就是所求作的三角形吗?
⑵ 剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?
Rt△ABC≌
A
B
C
∟
A'
B'
C'
c
a
∟
a
c
斜边、直角边公理
斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边”
或“HL”
斜边、直角边公理 (HL)
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ 中
AB=
BC=
∴Rt△ABC≌
∵∠C=∠C′=90°
斜边和一条直角边对应相等的两个直角三角形全等.
想一想 议一议
你能够用几种方法说明两个直角三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.
活动四
例题1:如图:AC⊥BC,BD⊥AD,AC=BD.求证:BC=AD.
A
B
C
D
O
在Rt△ACB和Rt△BDA中,则
AB=BA(共公边)
AC=BD.(已知)
∴ Rt△ACB≌Rt△BDA (HL).
∴BC=AD
(全等三角形对应边相等).
证明:∵ AC⊥BC,BD⊥AD
∴ ∠D=∠C=90°
练一练
2.如图,AB=CD,AE⊥BC,
DF⊥BC,CE=BF.
求证:AE=DF.
C
D
F
E
A
B
1. 如图,AC=AD,∠C,∠D是直角,求证: BC=BD
C
D
A
B
活动五 课堂测试
C
D
A
B
C
D
A
B
A
B
C
E
D
小结
直角三角形 全等的条件:
1)定义法;
SSS;
SAS;
ASA;
AAS.
2)解题中常用的4种方法
3)HL
直角三角形全等用
一般不用
这节课你有什么收获呢?
