人教版八年级数学上册15.1.1从分数到分式课件(25张)
文档属性
| 名称 | 人教版八年级数学上册15.1.1从分数到分式课件(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 10:30:01 | ||
图片预览






文档简介
整式
多项式
单项式、多项式统称整式
单项式
是单项式,也是整式
(
)
是多项式,也是整式
(
)
既不是单项式又不是多项式,即不是整式的另一类式子
温故而知新
x
x
15.1.1从分数到分式
学习目标
1.了解分式的概念;
2.理解分式有意义的条件及分式值为零的条件.(重点)
3.能熟练地求出分式有意义的条件及分式的值为零的条件.(难点)
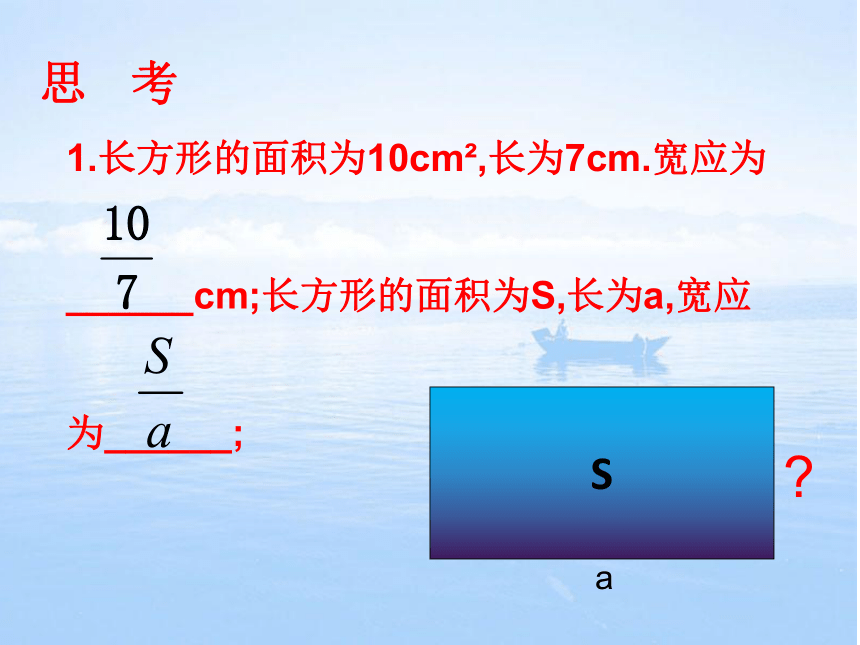
1.长方形的面积为10cm?,长为7cm.宽应为
______cm;长方形的面积为S,长为a,宽应
为______;
S
a
?
思
考
2.把体积为200cm?的水倒入底面积为
33cm?的
圆柱形容器中,水面高度为_____cm;把体积为V的
水倒入底面积为S的圆柱形容器中,
水面高度为______;
V
S
思
考
观察式子 和 ,
和
,
辨析它们的相同点和不同点.
都具有分数的形式
相同点
不同点
(观察分母)
分母中有无字母
?辨析、思考
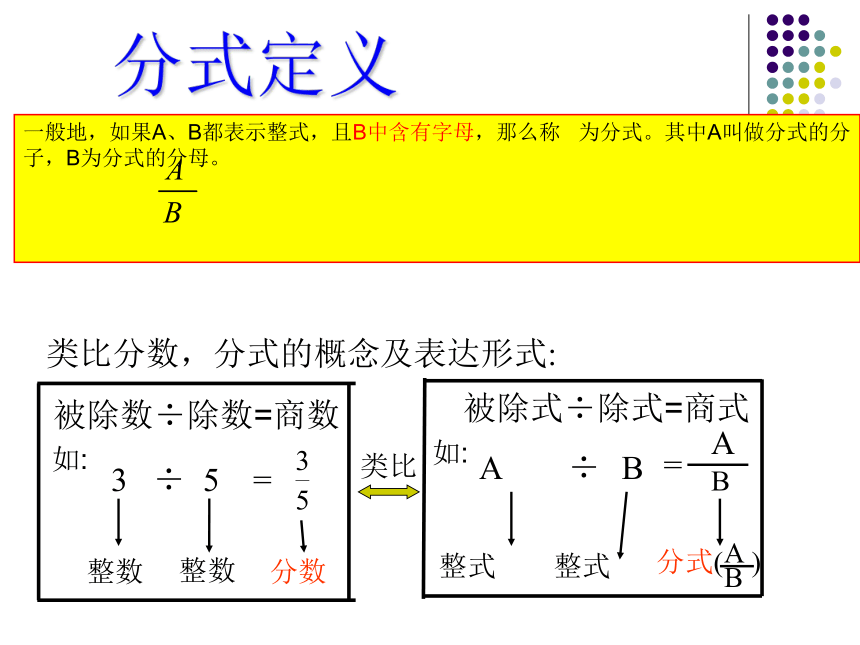
分式定义
类比分数,分式的概念及表达形式:
整数
整数
分数
B
整式
整式
类比
A
÷
B
=
A
3
÷
5
=
被除数÷除数=商数
如:
被除式÷除式=商式
如:
A
分式(
)
B
一般地,如果A、B都表示整式,且B中含有字母,那么称
为分式。其中A叫做分式的分子,B为分式的分母。
判断:下面的式子哪些是分式?
分式:
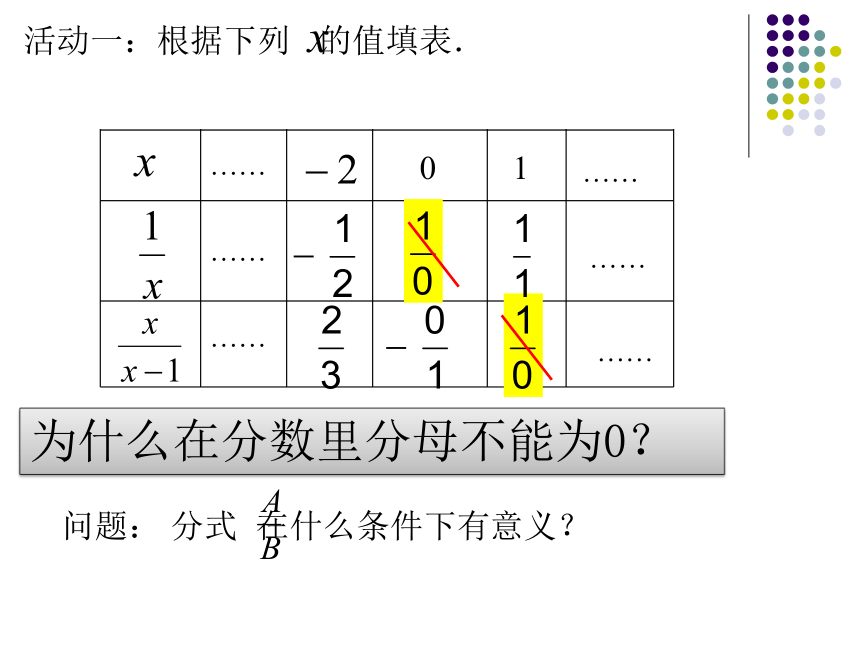
活动一:根据下列
的值填表.
……
……
……
……
……
……
0
1
问题:
分式
在什么条件下有意义?
问题:
分数在什么条件下有意义?
为什么在分数里分母不能为0?
1、分式
的分母有什么条件限制?
当B=0时,分式
无意义。
当B≠0时,分式
有意义。
探
究
例2
下列分式中的字母满足什么条件时分式有意义?
(1)
(2)
(3)
(4)
练习:当x取什么值时,下列分式有意义?
解⑴:
由分母
x-2≠0,得
x
≠
2。
所以当
x≠2时,
解⑵
:
由分母
4x+1
≠
0,得
x
≠
-
。
解
⑶
:
由分母|x|-3
≠
0,得
x
≠
±3
。
所以当x≠
±3时,
分式
有意义。
所以当
x≠-
时,
分式
有意义。
分式
有意义。
活动二:分式
在什么条件下值为0?
归纳:
分式的值要为0,需满足的条件是:分子的值等于0且分母值不为0.
分式为0的条件
解:当分子等于零而分母不等于零时,分式的值为零.
的值为零.
∴当x
=
1时分式
∴
x
≠
-1.
而 x+1≠0,
∴x
=
±1,
则 x2
-
1=0,
例2
当x为何值时,分式
的值为零?
(2)
当x为何值时,分式有意义?
(1)
当x为何值时,分式无意义?
例1.
已知分式
,
(2)由(1)得
当x
≠-2时,分式有意义
∴当x
=
-2时分式:
解:(1)当分母等于零时,分式无意义。
无意义。
∴
x
=
-2
即
x+2=0
(4)
当x=
-
3时,分式的值是多少?
(3)
当x为何值时,分式的值为零?
(4)当x
=
-3时,
解:(3)当分子等于零而分母不等于零时,分式的值为零。
的值为零。
∴当x
=
2时分式
∴
x
≠
-2
而 x+2≠0
∴x
=
±2
则 x2
-
4=0
(2)
当x为何值时,分式有意义?
(1)
当x为何值时,分式无意义?
(补充).已知分式
,
(3)
当x为何值时,分式的值为零?
三种形式
2.当
=0时,分子和分母应满足什么条件?
当A=0而B≠0时,分式
的值为零.
巧学速记:
分式形状像分数,
分母为零无意义,
分式的值要为零,
分子为零母不零,
二者缺一都不行。
分式
在什么条件下值为正?
归纳
(1)当A、B同号时,分式
的值为正;
(2)当A、B同号时,分式
的值为负.
下列式子中,哪些是分式,哪些是整式?
①
?
②
?
③?
④
?
⑤?
⑥
?
⑦?
解:整式有:②④⑦;分式有:①③⑤⑥.
若分式
无意义,求a的取值.
当x为任意实数时,下列分式一定有意义的是(
)
(B)
(
C)
(D)
B
w
(A)
1、当x为何值时,代数式
有意义?
2、当x为何值时,分式
无意义?
3、当x为何值时,分式
的值为零?
4、x为何整数时,分式
的值为整数?
X≥1且x≠5
x≠3且x≠-1
X=1
X=-13,-7,-5,-4,-3,-2,0,1,2,3,5,11
5、
请编制一个分式。使它的分子为x+4,且当它在x≠2时才有意义。
分式
定义
值为零的条件
有意义的条件
值为
正负
(1)当A、B同号时,分式
的值为正;
(2)当A、B同号时,分式
的值为负.
分式
值为零的条件是A=0且B
≠0.
分式
有意义的条件是B
≠0.
一般地,如果A,B表示整式,且B中含有字母,式子
叫做分式,其中,A叫做分式的分子,B叫做分式的分母.
多项式
单项式、多项式统称整式
单项式
是单项式,也是整式
(
)
是多项式,也是整式
(
)
既不是单项式又不是多项式,即不是整式的另一类式子
温故而知新
x
x
15.1.1从分数到分式
学习目标
1.了解分式的概念;
2.理解分式有意义的条件及分式值为零的条件.(重点)
3.能熟练地求出分式有意义的条件及分式的值为零的条件.(难点)
1.长方形的面积为10cm?,长为7cm.宽应为
______cm;长方形的面积为S,长为a,宽应
为______;
S
a
?
思
考
2.把体积为200cm?的水倒入底面积为
33cm?的
圆柱形容器中,水面高度为_____cm;把体积为V的
水倒入底面积为S的圆柱形容器中,
水面高度为______;
V
S
思
考
观察式子 和 ,
和
,
辨析它们的相同点和不同点.
都具有分数的形式
相同点
不同点
(观察分母)
分母中有无字母
?辨析、思考
分式定义
类比分数,分式的概念及表达形式:
整数
整数
分数
B
整式
整式
类比
A
÷
B
=
A
3
÷
5
=
被除数÷除数=商数
如:
被除式÷除式=商式
如:
A
分式(
)
B
一般地,如果A、B都表示整式,且B中含有字母,那么称
为分式。其中A叫做分式的分子,B为分式的分母。
判断:下面的式子哪些是分式?
分式:
活动一:根据下列
的值填表.
……
……
……
……
……
……
0
1
问题:
分式
在什么条件下有意义?
问题:
分数在什么条件下有意义?
为什么在分数里分母不能为0?
1、分式
的分母有什么条件限制?
当B=0时,分式
无意义。
当B≠0时,分式
有意义。
探
究
例2
下列分式中的字母满足什么条件时分式有意义?
(1)
(2)
(3)
(4)
练习:当x取什么值时,下列分式有意义?
解⑴:
由分母
x-2≠0,得
x
≠
2。
所以当
x≠2时,
解⑵
:
由分母
4x+1
≠
0,得
x
≠
-
。
解
⑶
:
由分母|x|-3
≠
0,得
x
≠
±3
。
所以当x≠
±3时,
分式
有意义。
所以当
x≠-
时,
分式
有意义。
分式
有意义。
活动二:分式
在什么条件下值为0?
归纳:
分式的值要为0,需满足的条件是:分子的值等于0且分母值不为0.
分式为0的条件
解:当分子等于零而分母不等于零时,分式的值为零.
的值为零.
∴当x
=
1时分式
∴
x
≠
-1.
而 x+1≠0,
∴x
=
±1,
则 x2
-
1=0,
例2
当x为何值时,分式
的值为零?
(2)
当x为何值时,分式有意义?
(1)
当x为何值时,分式无意义?
例1.
已知分式
,
(2)由(1)得
当x
≠-2时,分式有意义
∴当x
=
-2时分式:
解:(1)当分母等于零时,分式无意义。
无意义。
∴
x
=
-2
即
x+2=0
(4)
当x=
-
3时,分式的值是多少?
(3)
当x为何值时,分式的值为零?
(4)当x
=
-3时,
解:(3)当分子等于零而分母不等于零时,分式的值为零。
的值为零。
∴当x
=
2时分式
∴
x
≠
-2
而 x+2≠0
∴x
=
±2
则 x2
-
4=0
(2)
当x为何值时,分式有意义?
(1)
当x为何值时,分式无意义?
(补充).已知分式
,
(3)
当x为何值时,分式的值为零?
三种形式
2.当
=0时,分子和分母应满足什么条件?
当A=0而B≠0时,分式
的值为零.
巧学速记:
分式形状像分数,
分母为零无意义,
分式的值要为零,
分子为零母不零,
二者缺一都不行。
分式
在什么条件下值为正?
归纳
(1)当A、B同号时,分式
的值为正;
(2)当A、B同号时,分式
的值为负.
下列式子中,哪些是分式,哪些是整式?
①
?
②
?
③?
④
?
⑤?
⑥
?
⑦?
解:整式有:②④⑦;分式有:①③⑤⑥.
若分式
无意义,求a的取值.
当x为任意实数时,下列分式一定有意义的是(
)
(B)
(
C)
(D)
B
w
(A)
1、当x为何值时,代数式
有意义?
2、当x为何值时,分式
无意义?
3、当x为何值时,分式
的值为零?
4、x为何整数时,分式
的值为整数?
X≥1且x≠5
x≠3且x≠-1
X=1
X=-13,-7,-5,-4,-3,-2,0,1,2,3,5,11
5、
请编制一个分式。使它的分子为x+4,且当它在x≠2时才有意义。
分式
定义
值为零的条件
有意义的条件
值为
正负
(1)当A、B同号时,分式
的值为正;
(2)当A、B同号时,分式
的值为负.
分式
值为零的条件是A=0且B
≠0.
分式
有意义的条件是B
≠0.
一般地,如果A,B表示整式,且B中含有字母,式子
叫做分式,其中,A叫做分式的分子,B叫做分式的分母.
