一元二次方程的定义与解法
图片预览






文档简介
(共16张PPT)
第17章 一元二次方程及其解法
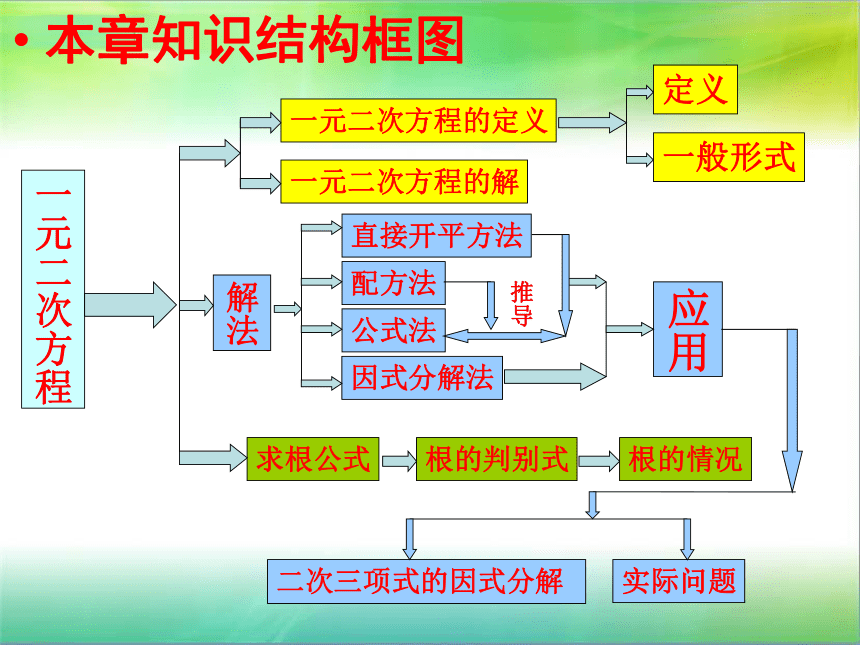
本章知识结构框图
一元二次方程
一元二次方程的定义
定义
一般形式
一元二次方程的解
解法
直接开平方法
配方法
因式分解法
公式法
求根公式
根的判别式
根的情况
二次三项式的因式分解
实际问题
应用
推导
一 . 一元二次方程的概念
知识点1 .定义:只含有一个未知数,且未知数的最高次数是2的整式方程叫做一元二次方程。
说明:
判断一个方程是否是一元二次方程时,先要观察其是否属于整式方程,再看其整理合并后是否符合: 只含一个未知数, 未知数的最高次数是2.
例题1:下列式子中哪些不是一元二次方程?并说明理由
(1)
(2)
(3)
(4)
(8)
(7)
(6)
(5)
(a,b为已知数)
例题2:
当m取何值时,方程 是一元二次方程.
知识点2 一元二次方程的一般形式:
说明:
(1)a≠0是一元二次方程一般形式的一个重要组成部分;
(2)任何一个一元二次方程经过整理(去分母,去括号,移项,合并同类项)都可化为一般形式,我们说一元二次方程的二次项,二次项系数,一次项,一次项系数,常数项都是对化为一般形式以后而言的;
(3)注意区分二次项和二次项系数,一次项和一次项系数,它们都包含前面的符号。
例题3:
将下列关于x的一元二次方程化为一般形式,再说出方程中的各项与各项系数。
(1)
(2)
(3)
(4)
知识点3:
一元二次方程的解(根):能使一元二次方程左,右两边都相等的未知数的值,称为一元二次方程的解(根)。
说明:
一元二次方程的解类同与一元一次方程的解,通常把未知数的值代入方程,若是方程的解即可使等式成立。
例题1: 判断方程后面括号里的数是否是方程的解:
(2)
(1)
例题2: 是不是一元二次方程 的根。
例题3:关于x的一元二次方程
有一个根是0,求
的值。
试一试,你一定可以!
一 . 基础练习
1. 一元二次方程的一般形式是______________。
2. 下列方程中是一元二次方程的是______。
( a 为实数 )
3. 一元二次方程 的二次项系数,一次项系数,常数项分别是_______。
4 。 已知一个一元二次方程的两个根分别是2,-5,那么这个方程是________。
5. 当m____ 值时, 是一元二次方程?
二. 能力提升
6. 将下列方程化为一般形式,并写出二次项系数,一次项系数,常数项。
(1)
(6)
(3)
(2)
(4)
(5)
8. 已知关于x的方程 各项系数的和等于5,求m的值
9. 写出一个一元二次方程,使这个方程的一个根是-1,它的二次项系数为2,并说明有一个根为-1一元二次方程具有什么特征。
7. 如果2是一元二次方程 的一个根,那么常数b的值为___。
二. 一元二次方程的解法
知识点1 直接开平方法
如果一元二次方程的一边含有未知数的代数式的平方,另一边是一个非负数的常数,那么就可以直接用开平方法求解,这种方法适合 形式求解。
说明:
直接开平方法的理论依据是平方根的定义及其性质,直接开平方法适用于解 形如 的方程 ;
形如 的一元二次方程。
例题1:
用直接开平方法解下列方程。
(1)
(2)
(3)
(4)
知识点2 因式分解法
1.因式分解法的定义:运用因式分解的手段求一元二次方程根的方法叫做因式分解法
3.用因式分解法解一元二次方程的一般步骤:
(1)将方程右边化为0;(2)将方程左边的二次三项式分解成两个一次因式的乘积;(3)令每一个一次因式分别等于0,得到两个一元一次方程;(4)分别解这两个一元一次方程,它们的解就是原方程的根。
例题:
用因式分解法解下列方程。
2.因式分解法的理论依据是:若两个因式的积等于0,则这两个因式中至少有一个等于0,将一元二次方程分解成A B=0,则A=0或B=0。
1.
3.
5.
2.
6.
4.
知识点3 配方法
1. 定义:先把方程中的常数项移到方程的右边,把左边配成完全平方式,然后用直接开平方法求出一元二次方程的根的解法叫做配方法。
2. 配方法的理论依据是完全平方公式:
3.用配方法解一元二次方程 的一般步骤:
(1)把二次项系数化为1:方程两边同时除以二次项系数;
(2) 移项:把常数项移到方程右边;
(3) 配方:方程两边都加上一次项系数一半的平方,把原方程化为
的形式;
(4) 当k≥0时,用直接开平方的方法解。
例题:
用配方法解下列方程:
(1)
(2)
(3)
(4)
1.一元二次方程的一般形式是_________
它的求根公式是 ________,
根的判别式是△=________
△___时 方程有两个不相等的实数根;
△___时 方程有两个相等的实数根;
△__时 方程无实数根。
<
<
知识点4 公式法
> 0
<
= 0
< 0
2.用公式法解一元二次方程的一般步骤:
(1)把一元二次方程化为一般形式;(2)确定a,b,c的值;(3)求出△的值;(4)若△≥0,方程有两个根,写出两根;若△<0,则方程无解。
例题:
用公式法解下列方程。
(2)
(4)
(3)
(1)
解:
a=1 , b=7 , c=3
△=
解:
解:
解:
原方程变形为:
原方程变形为:
原方程变形为:
△=
△=
△=
a=4, b=4 , c=-1
a=2 , b=-6 , c=-3
a=6, b=-1 , c=-3
∴
∴
∴
∴
试一试,你一定可以!
用适当的方法解下列方程:
答案:
答案:
答案:
答案:
(1)
(3)
(2)
(4)
(5)
(13)
(7)
(9)
(11)
(12)
(10)
(8)
(6)
(14)
解答略
第17章 一元二次方程及其解法
本章知识结构框图
一元二次方程
一元二次方程的定义
定义
一般形式
一元二次方程的解
解法
直接开平方法
配方法
因式分解法
公式法
求根公式
根的判别式
根的情况
二次三项式的因式分解
实际问题
应用
推导
一 . 一元二次方程的概念
知识点1 .定义:只含有一个未知数,且未知数的最高次数是2的整式方程叫做一元二次方程。
说明:
判断一个方程是否是一元二次方程时,先要观察其是否属于整式方程,再看其整理合并后是否符合: 只含一个未知数, 未知数的最高次数是2.
例题1:下列式子中哪些不是一元二次方程?并说明理由
(1)
(2)
(3)
(4)
(8)
(7)
(6)
(5)
(a,b为已知数)
例题2:
当m取何值时,方程 是一元二次方程.
知识点2 一元二次方程的一般形式:
说明:
(1)a≠0是一元二次方程一般形式的一个重要组成部分;
(2)任何一个一元二次方程经过整理(去分母,去括号,移项,合并同类项)都可化为一般形式,我们说一元二次方程的二次项,二次项系数,一次项,一次项系数,常数项都是对化为一般形式以后而言的;
(3)注意区分二次项和二次项系数,一次项和一次项系数,它们都包含前面的符号。
例题3:
将下列关于x的一元二次方程化为一般形式,再说出方程中的各项与各项系数。
(1)
(2)
(3)
(4)
知识点3:
一元二次方程的解(根):能使一元二次方程左,右两边都相等的未知数的值,称为一元二次方程的解(根)。
说明:
一元二次方程的解类同与一元一次方程的解,通常把未知数的值代入方程,若是方程的解即可使等式成立。
例题1: 判断方程后面括号里的数是否是方程的解:
(2)
(1)
例题2: 是不是一元二次方程 的根。
例题3:关于x的一元二次方程
有一个根是0,求
的值。
试一试,你一定可以!
一 . 基础练习
1. 一元二次方程的一般形式是______________。
2. 下列方程中是一元二次方程的是______。
( a 为实数 )
3. 一元二次方程 的二次项系数,一次项系数,常数项分别是_______。
4 。 已知一个一元二次方程的两个根分别是2,-5,那么这个方程是________。
5. 当m____ 值时, 是一元二次方程?
二. 能力提升
6. 将下列方程化为一般形式,并写出二次项系数,一次项系数,常数项。
(1)
(6)
(3)
(2)
(4)
(5)
8. 已知关于x的方程 各项系数的和等于5,求m的值
9. 写出一个一元二次方程,使这个方程的一个根是-1,它的二次项系数为2,并说明有一个根为-1一元二次方程具有什么特征。
7. 如果2是一元二次方程 的一个根,那么常数b的值为___。
二. 一元二次方程的解法
知识点1 直接开平方法
如果一元二次方程的一边含有未知数的代数式的平方,另一边是一个非负数的常数,那么就可以直接用开平方法求解,这种方法适合 形式求解。
说明:
直接开平方法的理论依据是平方根的定义及其性质,直接开平方法适用于解 形如 的方程 ;
形如 的一元二次方程。
例题1:
用直接开平方法解下列方程。
(1)
(2)
(3)
(4)
知识点2 因式分解法
1.因式分解法的定义:运用因式分解的手段求一元二次方程根的方法叫做因式分解法
3.用因式分解法解一元二次方程的一般步骤:
(1)将方程右边化为0;(2)将方程左边的二次三项式分解成两个一次因式的乘积;(3)令每一个一次因式分别等于0,得到两个一元一次方程;(4)分别解这两个一元一次方程,它们的解就是原方程的根。
例题:
用因式分解法解下列方程。
2.因式分解法的理论依据是:若两个因式的积等于0,则这两个因式中至少有一个等于0,将一元二次方程分解成A B=0,则A=0或B=0。
1.
3.
5.
2.
6.
4.
知识点3 配方法
1. 定义:先把方程中的常数项移到方程的右边,把左边配成完全平方式,然后用直接开平方法求出一元二次方程的根的解法叫做配方法。
2. 配方法的理论依据是完全平方公式:
3.用配方法解一元二次方程 的一般步骤:
(1)把二次项系数化为1:方程两边同时除以二次项系数;
(2) 移项:把常数项移到方程右边;
(3) 配方:方程两边都加上一次项系数一半的平方,把原方程化为
的形式;
(4) 当k≥0时,用直接开平方的方法解。
例题:
用配方法解下列方程:
(1)
(2)
(3)
(4)
1.一元二次方程的一般形式是_________
它的求根公式是 ________,
根的判别式是△=________
△___时 方程有两个不相等的实数根;
△___时 方程有两个相等的实数根;
△__时 方程无实数根。
<
<
知识点4 公式法
> 0
<
= 0
< 0
2.用公式法解一元二次方程的一般步骤:
(1)把一元二次方程化为一般形式;(2)确定a,b,c的值;(3)求出△的值;(4)若△≥0,方程有两个根,写出两根;若△<0,则方程无解。
例题:
用公式法解下列方程。
(2)
(4)
(3)
(1)
解:
a=1 , b=7 , c=3
△=
解:
解:
解:
原方程变形为:
原方程变形为:
原方程变形为:
△=
△=
△=
a=4, b=4 , c=-1
a=2 , b=-6 , c=-3
a=6, b=-1 , c=-3
∴
∴
∴
∴
试一试,你一定可以!
用适当的方法解下列方程:
答案:
答案:
答案:
答案:
(1)
(3)
(2)
(4)
(5)
(13)
(7)
(9)
(11)
(12)
(10)
(8)
(6)
(14)
解答略
