人教版八年级数学上册课件:14.2.2完全平方公式(28张)
文档属性
| 名称 | 人教版八年级数学上册课件:14.2.2完全平方公式(28张) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 10:32:59 | ||
图片预览

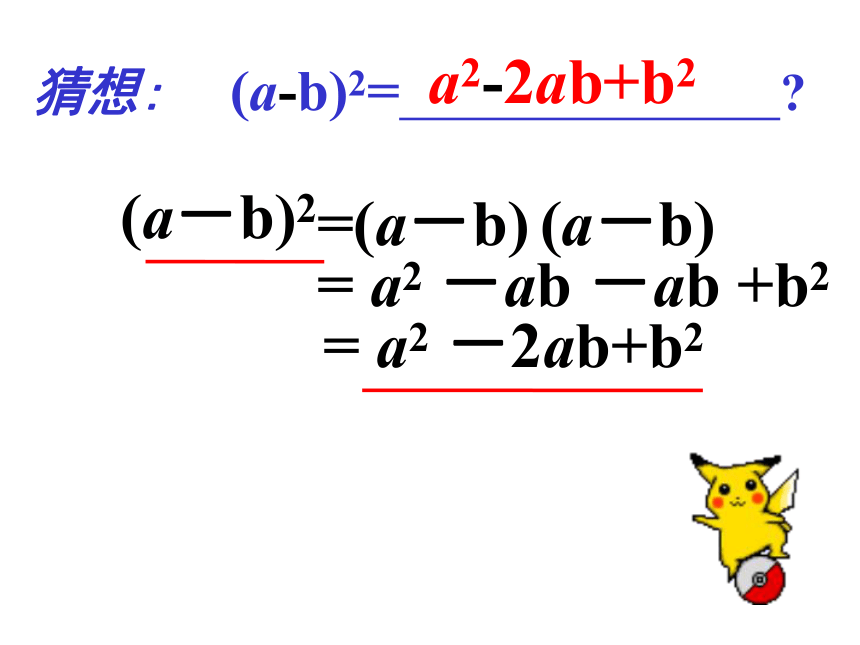





文档简介
14.2.2完全平方公式
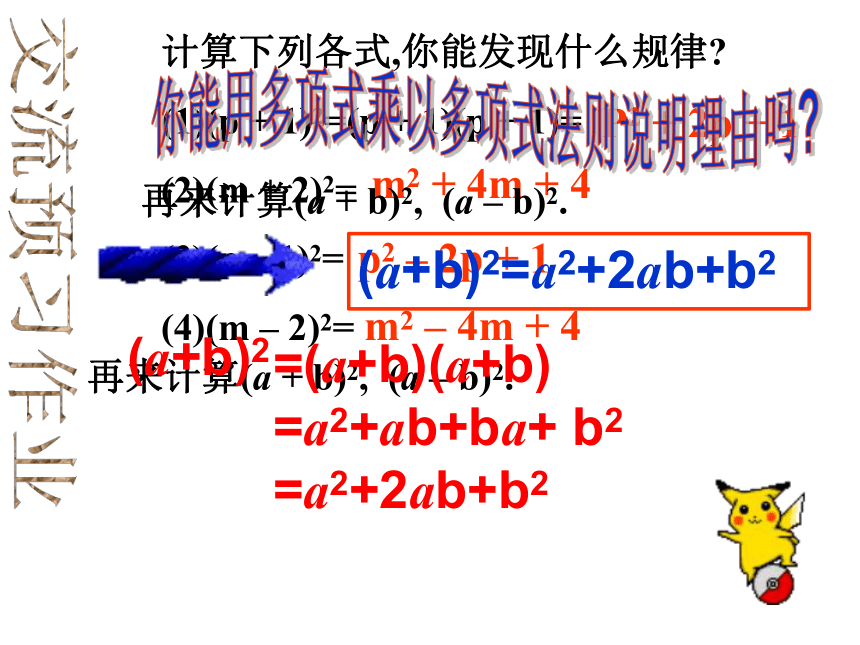
计算下列各式,你能发现什么规律?
(p + 1)2=(p + 1)(p + 1)=
(2)(m + 2)2=
(3)(p – 1)2=
(4)(m – 2)2=
P2 + 2p + 1
m2 + 4m + 4
p2 – 2p + 1
m2 – 4m + 4
再来计算(a + b)2, (a – b)2.
再来计算(a + b)2, (a – b)2.
=(a+b)(a+b)
=a2+ab+ba+ b2
=a2+2ab+b2
(a+b)2
(a+b)2=a2+2ab+b2
(a-b)2
= a2 -2ab+b2
= a2 -ab -ab +b2
=(a-b) (a-b)
猜想: (a-b)2= ?
a2-2ab+b2
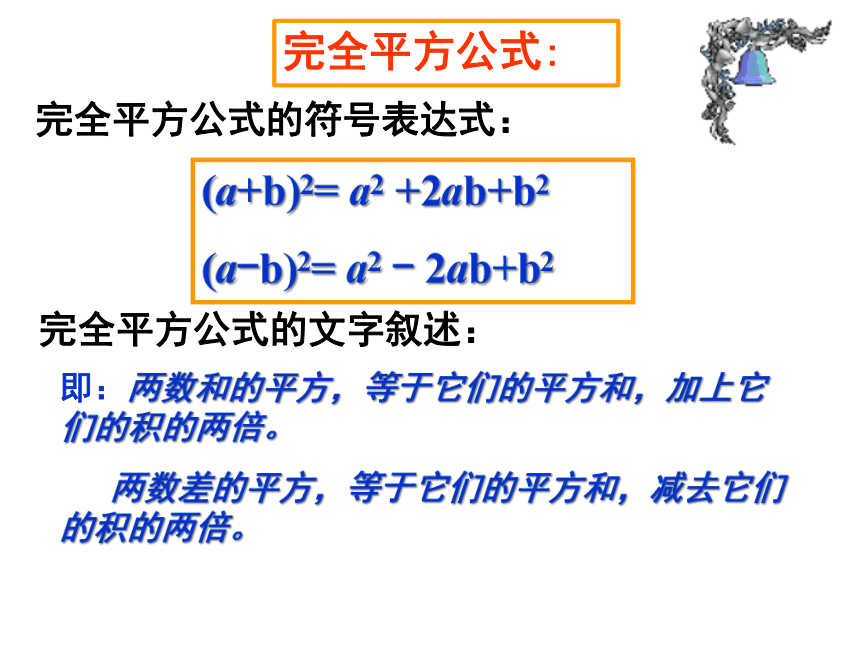
完全平方公式:
即:两数和的平方,等于它们的平方和,加上它们的积的两倍。
两数差的平方,等于它们的平方和,减去它们的积的两倍。
完全平方公式的文字叙述:
完全平方公式的符号表达式:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
(a ± b)2=a2±2ab+b2
记忆口诀:
首平方,尾平方,
积的2倍放中间,
中间符号中间定
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式
中间的符号相同。
1.下面各式的计算错在哪里?怎样改正?
(1) (a+ b)2 = a2 +b2;
(2) (a – b) 2 =a2 – b2.
(3)
例题解析
例1 利用完全平方公式计算:
(1) (2x?3)2 ; (2) (4x+5y)2 ; (3) (mn?a)2
使用完全平方公式与平方差公式的使用一样,
注意
?
先把要计算的式子与完全平方公式对照,
明确个是 a , 哪个是 b.
第一数
2x
4x2
2x
的平方,
( )2
?
减去
2x
第一数
与第二数
?
2x
3
?
乘积
的2倍,
?
2
加上
+
第二数
3
的平方.
2
=
?
12x
+
9 ;
解:(1) (2x?3)2
做题时要边念边写:
=
3
纠 错 练 习
指出下列各式中的错误,并加以改正:
(1) (2a?1)2=2a2?2a+1;
(2) (2a+1)2=4a2 +1;
(3) (?a?1)2=?a2?2a?1.
解: (1)
第一数被平方时, 没有添括号;
第一数与第二数乘积的2倍 少乘了一个2 ;
应改为: (2a?1)2= (2a)2?2?2a?1+1;
(2) 少了第一数与第二数乘积的2倍 (丢了一项);
应改为: (2a+1)2= (2a)2+2?2a?1 +1;
(3) 第一数平方没有添括号,
第一数与第二数乘积的2倍 错了符号;
第二数的平方 这一项错了符号;
应改为: (?a?1)2=(?a)2?2?(?a )?1+12;
例1、运用完全平方公式计算:
解: (4m+n)2=
=16m2
(1)(4m+n)2
(a +b)2= a2 + 2 a b + b2
(4m)2
+2?(4m) ?n
+n2
+8mn
+n2
例2 运用完全平方公式计算:
(1) 1022; (2) 992
解: (1) 1022 =
(100+2)2
变形
(2) 992=
=1002+2×100×2+22
=10000+400+4
=10404
(100-1)2=1002-2×100×1+12
=10000-200+1=9801
1.运用完全平方公式计算:
(1)(x+6)2; (2) (y-5)2;
(3) (-2x+5)2; (4) ( x - y)2.
一个正方形的边长增加了3厘米,面积相应增加了51平方厘米,求这个正方形的边长。
求:a、b的值
先化简,再求值:
随堂练习
随堂练习
(1) ( x ? 2y)2 ;
(2) (2xy+ x )2 ;
1、计算:
(3) (n +1)2 ? n2.
(1)(x+3)2=x2 +6x +9
3、在下面的计算中有些地方用纸牌盖上了,看谁能最快地说出纸牌下盖的是什么式子,我们来抢答一下!
猜猜我是谁!
(2)(2m-n)2=4m2 -4mn +n2
(3)(2x+3y)2=4x2+12xy+9y2
(4)(x- y)2=x2-xy+ y2
(2) (a - b)2 与 (b - a)2 、
(-b +a)2 与(-a +b)2
(1) (-a -b)2 与(a+b)2
思考:比较下列各式之间的关系:
相等
相等
计算:(-x-2y)2
让我们大家一起来想!
1、如果x2-6x+N是一个完全平方式,那么N是( )
(A )-3 (B)3 (C)-9 (D)9
D
2、如果x2-Nx+9是一个完全平方式,那么N是( )
(A )-6 (B)6 (C) ±6 (D) ±9
C
完全平方公式 a2+b2 =(a+b)2 -2ab
若a+b=5,ab=6 求: a2+3ab+b2的值。
(a ± b)2=a2±2ab+b2
解:a2+3ab+b2
=a2+2ab+b2+ab
=(a+b)2+ab
把a+b=5,ab=6代入上式
得:52+6=25+6=31
填一填:
1、如果 x?+ax+16 是一个完全平方式, 则a=___
+8
∵
∴
×
×
2、如果 25a?-30ab+m 是一个完全平方式,则 m=___
填一填:
9b2
∵
∴
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
练习:
已知:
求: 和 的值
1.已知x+y=5,xy=6,求
(1)x2+y2 (2)x-y的值
2.设a-b=3,ab=2,求a?+b?的值。
3. a2+b2-2a+6b+10=0,求a+b的值
计算下列各式,你能发现什么规律?
(p + 1)2=(p + 1)(p + 1)=
(2)(m + 2)2=
(3)(p – 1)2=
(4)(m – 2)2=
P2 + 2p + 1
m2 + 4m + 4
p2 – 2p + 1
m2 – 4m + 4
再来计算(a + b)2, (a – b)2.
再来计算(a + b)2, (a – b)2.
=(a+b)(a+b)
=a2+ab+ba+ b2
=a2+2ab+b2
(a+b)2
(a+b)2=a2+2ab+b2
(a-b)2
= a2 -2ab+b2
= a2 -ab -ab +b2
=(a-b) (a-b)
猜想: (a-b)2= ?
a2-2ab+b2
完全平方公式:
即:两数和的平方,等于它们的平方和,加上它们的积的两倍。
两数差的平方,等于它们的平方和,减去它们的积的两倍。
完全平方公式的文字叙述:
完全平方公式的符号表达式:
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
(a ± b)2=a2±2ab+b2
记忆口诀:
首平方,尾平方,
积的2倍放中间,
中间符号中间定
公式特点:
4、公式中的字母a,b可以表示数,单项式和
多项式。
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
1、积为二次三项式;
2、积中两项为两数的平方和;
3、另一项是两数积的2倍,且与乘式
中间的符号相同。
1.下面各式的计算错在哪里?怎样改正?
(1) (a+ b)2 = a2 +b2;
(2) (a – b) 2 =a2 – b2.
(3)
例题解析
例1 利用完全平方公式计算:
(1) (2x?3)2 ; (2) (4x+5y)2 ; (3) (mn?a)2
使用完全平方公式与平方差公式的使用一样,
注意
?
先把要计算的式子与完全平方公式对照,
明确个是 a , 哪个是 b.
第一数
2x
4x2
2x
的平方,
( )2
?
减去
2x
第一数
与第二数
?
2x
3
?
乘积
的2倍,
?
2
加上
+
第二数
3
的平方.
2
=
?
12x
+
9 ;
解:(1) (2x?3)2
做题时要边念边写:
=
3
纠 错 练 习
指出下列各式中的错误,并加以改正:
(1) (2a?1)2=2a2?2a+1;
(2) (2a+1)2=4a2 +1;
(3) (?a?1)2=?a2?2a?1.
解: (1)
第一数被平方时, 没有添括号;
第一数与第二数乘积的2倍 少乘了一个2 ;
应改为: (2a?1)2= (2a)2?2?2a?1+1;
(2) 少了第一数与第二数乘积的2倍 (丢了一项);
应改为: (2a+1)2= (2a)2+2?2a?1 +1;
(3) 第一数平方没有添括号,
第一数与第二数乘积的2倍 错了符号;
第二数的平方 这一项错了符号;
应改为: (?a?1)2=(?a)2?2?(?a )?1+12;
例1、运用完全平方公式计算:
解: (4m+n)2=
=16m2
(1)(4m+n)2
(a +b)2= a2 + 2 a b + b2
(4m)2
+2?(4m) ?n
+n2
+8mn
+n2
例2 运用完全平方公式计算:
(1) 1022; (2) 992
解: (1) 1022 =
(100+2)2
变形
(2) 992=
=1002+2×100×2+22
=10000+400+4
=10404
(100-1)2=1002-2×100×1+12
=10000-200+1=9801
1.运用完全平方公式计算:
(1)(x+6)2; (2) (y-5)2;
(3) (-2x+5)2; (4) ( x - y)2.
一个正方形的边长增加了3厘米,面积相应增加了51平方厘米,求这个正方形的边长。
求:a、b的值
先化简,再求值:
随堂练习
随堂练习
(1) ( x ? 2y)2 ;
(2) (2xy+ x )2 ;
1、计算:
(3) (n +1)2 ? n2.
(1)(x+3)2=x2 +6x +9
3、在下面的计算中有些地方用纸牌盖上了,看谁能最快地说出纸牌下盖的是什么式子,我们来抢答一下!
猜猜我是谁!
(2)(2m-n)2=4m2 -4mn +n2
(3)(2x+3y)2=4x2+12xy+9y2
(4)(x- y)2=x2-xy+ y2
(2) (a - b)2 与 (b - a)2 、
(-b +a)2 与(-a +b)2
(1) (-a -b)2 与(a+b)2
思考:比较下列各式之间的关系:
相等
相等
计算:(-x-2y)2
让我们大家一起来想!
1、如果x2-6x+N是一个完全平方式,那么N是( )
(A )-3 (B)3 (C)-9 (D)9
D
2、如果x2-Nx+9是一个完全平方式,那么N是( )
(A )-6 (B)6 (C) ±6 (D) ±9
C
完全平方公式 a2+b2 =(a+b)2 -2ab
若a+b=5,ab=6 求: a2+3ab+b2的值。
(a ± b)2=a2±2ab+b2
解:a2+3ab+b2
=a2+2ab+b2+ab
=(a+b)2+ab
把a+b=5,ab=6代入上式
得:52+6=25+6=31
填一填:
1、如果 x?+ax+16 是一个完全平方式, 则a=___
+8
∵
∴
×
×
2、如果 25a?-30ab+m 是一个完全平方式,则 m=___
填一填:
9b2
∵
∴
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
练习:
已知:
求: 和 的值
1.已知x+y=5,xy=6,求
(1)x2+y2 (2)x-y的值
2.设a-b=3,ab=2,求a?+b?的值。
3. a2+b2-2a+6b+10=0,求a+b的值
