人教版八年级下册16.2.2 最简二次根式课件(30张)
文档属性
| 名称 | 人教版八年级下册16.2.2 最简二次根式课件(30张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 870.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览











文档简介
人教版数学教材八年级下
第16章 二次根式
16.2 最简二次根式
二次根式的性质
(1)
(2)
(3)
(4)
复习
问题苑
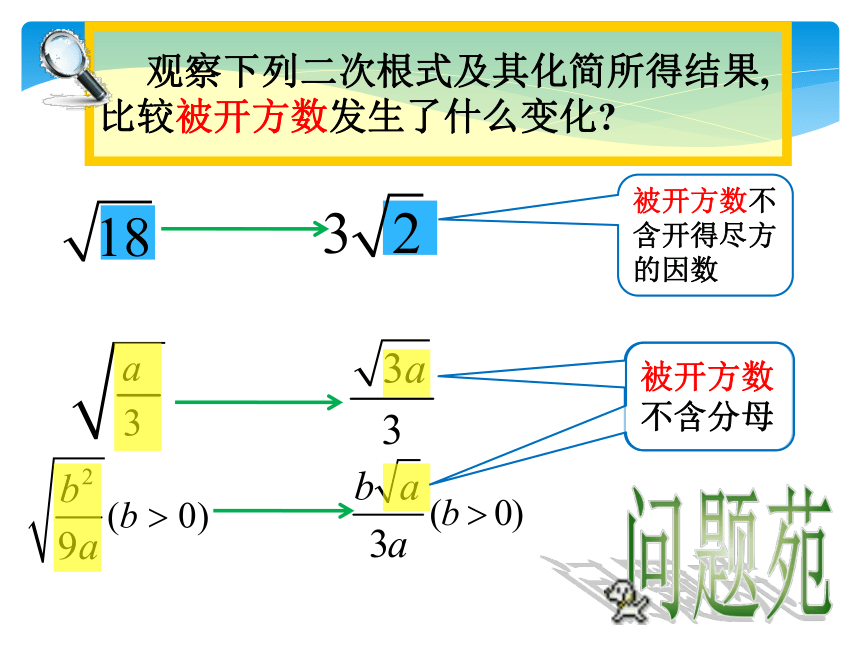
观察下列二次根式及其化简所得结果,比较被开方数发生了什么变化?
被开方数不含开得尽方的因数
被开方数不含分母
概念库
被开方数满足上述两个条件的二次根式,叫做最简二次根式.
(2)被开方数不含分母.
最简二次根式
如:
√
√
(1)被开方数各因式的指数都为1.
例题讲解
例1.判断下列二次根式是不是最简二次根式
解(1)因为被开方数 含分母3,
所以 不是最简二次根式.
(2)因为被开方数分解:
所以 是最简二次根式.
注:被开方数比较复杂时,
应先进行因式分解再观察
例2.将下列二次根式化成最简二次根式.
用它的正平方根代替后移到根号外面 .
&将被开方数中
解:由 和
得x≥0
原式=
解原式
&把被开方数(或式)化成积的形式,即分解因式
&将被开方数中的分母化去
解原式=
课外拓展
化简二次根式的步骤:
1.把被开方数分解因式(或因数) ;
2.将被开方数中开得尽方的因数(式)用它的正平方根代替后移到根号外面 .
3.将被开方数中的分母化去
4.被开方数是带分数或小数时要化成假分数.
判断下列各式是否为最简二次根式?
(5) ( );
(2) ( );
(3) ( );
(4) ( );
(1) ( );
(6) ( );
(7) ( );
√
×
×
×
×
×
√
辨析训练一
被开方数是多项式的要先分解因式再进行观察判断.
练习1.将下列二次根式化成最简二次根式.
(0练习2、 把下列各式化成最简二次根式:
(1) ;(2)
解(1)
(2)
把下列各式化成最简二次根式:
(1) (2)
(3) (4)
练习3
这节你学到了什么?
1.最简二次根式的概念.
满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中不含能开得尽方的因数或因式;
(2)被开方数不含分母。
2.如何化二次根式为最简二次根式 .
(1)把被开方数分解因式(或因数) ;
(2)将被开方数中开得尽方的因数(式)用它的正平方根代替后移到根号外面 .
(3)将被开方数中的分母化去
1、化简下列各式:
及时反馈
( )
B.
C.
D.
A.
D
分析:本题重点考察 的应用,这里关键是确定x
的符号,而 中隐含了-x3≥0,即x≤0,此时 。
由-x3≥0,得x≤0,
正解:
又x为分母不为0,
∴x<0
4、若aA. a+b B. a-b C. -a-b D. -a+b
D
3、实数 在数轴上的位置如图所示,化简:
1
及时反馈
5、实数 在数轴上的位置如图所示,化简:
-1
2
1
0
6、已知三角形的三边长分别是 a、b、c,且 ,那么 等于( )
A、2a-b B、2c-b
C、b-2a D、b-2c
D
及时反馈
正解:
8.若 ,则化简 = .
9.若代数式 的值是常数2,则a的取值范围是( )
A. B.
C. D.
二次根式化简
二次根式化简的常见错误
二次根式化简的常见错误
二次根式化简的常见错误
第16章 二次根式
16.2 最简二次根式
二次根式的性质
(1)
(2)
(3)
(4)
复习
问题苑
观察下列二次根式及其化简所得结果,比较被开方数发生了什么变化?
被开方数不含开得尽方的因数
被开方数不含分母
概念库
被开方数满足上述两个条件的二次根式,叫做最简二次根式.
(2)被开方数不含分母.
最简二次根式
如:
√
√
(1)被开方数各因式的指数都为1.
例题讲解
例1.判断下列二次根式是不是最简二次根式
解(1)因为被开方数 含分母3,
所以 不是最简二次根式.
(2)因为被开方数分解:
所以 是最简二次根式.
注:被开方数比较复杂时,
应先进行因式分解再观察
例2.将下列二次根式化成最简二次根式.
用它的正平方根代替后移到根号外面 .
&将被开方数中
解:由 和
得x≥0
原式=
解原式
&把被开方数(或式)化成积的形式,即分解因式
&将被开方数中的分母化去
解原式=
课外拓展
化简二次根式的步骤:
1.把被开方数分解因式(或因数) ;
2.将被开方数中开得尽方的因数(式)用它的正平方根代替后移到根号外面 .
3.将被开方数中的分母化去
4.被开方数是带分数或小数时要化成假分数.
判断下列各式是否为最简二次根式?
(5) ( );
(2) ( );
(3) ( );
(4) ( );
(1) ( );
(6) ( );
(7) ( );
√
×
×
×
×
×
√
辨析训练一
被开方数是多项式的要先分解因式再进行观察判断.
练习1.将下列二次根式化成最简二次根式.
(0
(1) ;(2)
解(1)
(2)
把下列各式化成最简二次根式:
(1) (2)
(3) (4)
练习3
这节你学到了什么?
1.最简二次根式的概念.
满足下列条件的二次根式,叫做最简二次根式。
(1)被开方数中不含能开得尽方的因数或因式;
(2)被开方数不含分母。
2.如何化二次根式为最简二次根式 .
(1)把被开方数分解因式(或因数) ;
(2)将被开方数中开得尽方的因数(式)用它的正平方根代替后移到根号外面 .
(3)将被开方数中的分母化去
1、化简下列各式:
及时反馈
( )
B.
C.
D.
A.
D
分析:本题重点考察 的应用,这里关键是确定x
的符号,而 中隐含了-x3≥0,即x≤0,此时 。
由-x3≥0,得x≤0,
正解:
又x为分母不为0,
∴x<0
4、若a
D
3、实数 在数轴上的位置如图所示,化简:
1
及时反馈
5、实数 在数轴上的位置如图所示,化简:
-1
2
1
0
6、已知三角形的三边长分别是 a、b、c,且 ,那么 等于( )
A、2a-b B、2c-b
C、b-2a D、b-2c
D
及时反馈
正解:
8.若 ,则化简 = .
9.若代数式 的值是常数2,则a的取值范围是( )
A. B.
C. D.
二次根式化简
二次根式化简的常见错误
二次根式化简的常见错误
二次根式化简的常见错误
