人教版八年级下册17.1.2 勾股定理的应用课件(30张)
文档属性
| 名称 | 人教版八年级下册17.1.2 勾股定理的应用课件(30张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 365.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览






文档简介
勾股定理的应用
回顾与思考
-----------勾股定理
1、直角三角形的边、角之间分别存在着什么关系?
2、请你举一个生活中的实例,并应用勾股定理解决它。
课堂练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( )
2.? ABC的a=6,b=8,则c=10 ( )
?
?
二填空题 1.在? ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______. 2.在? ABC中, C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.
6
8
41
24
4.8
3.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm
D
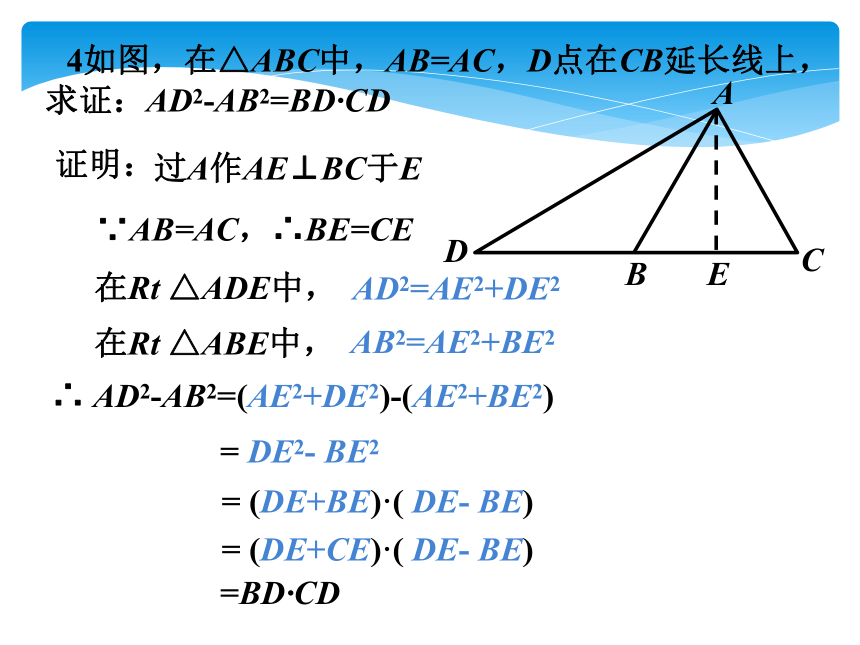
4如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
5、已知:数7和24,请你再写一个整数,
使这些数恰好是一个直角三角形三边的长,
则这个数可以是——
6、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是————
25
24
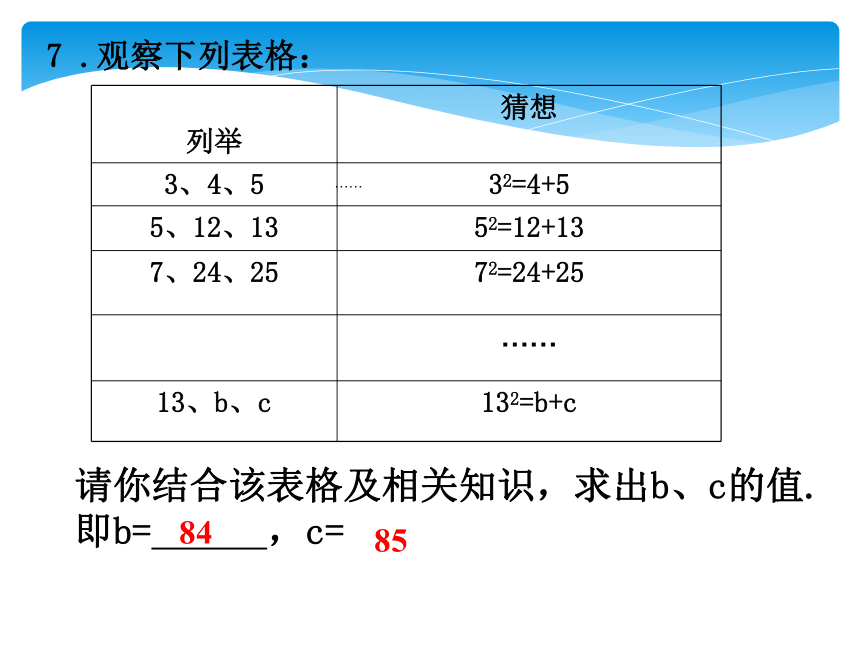
7 .观察下列表格:
……
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
……
13、b、c
132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
84
85
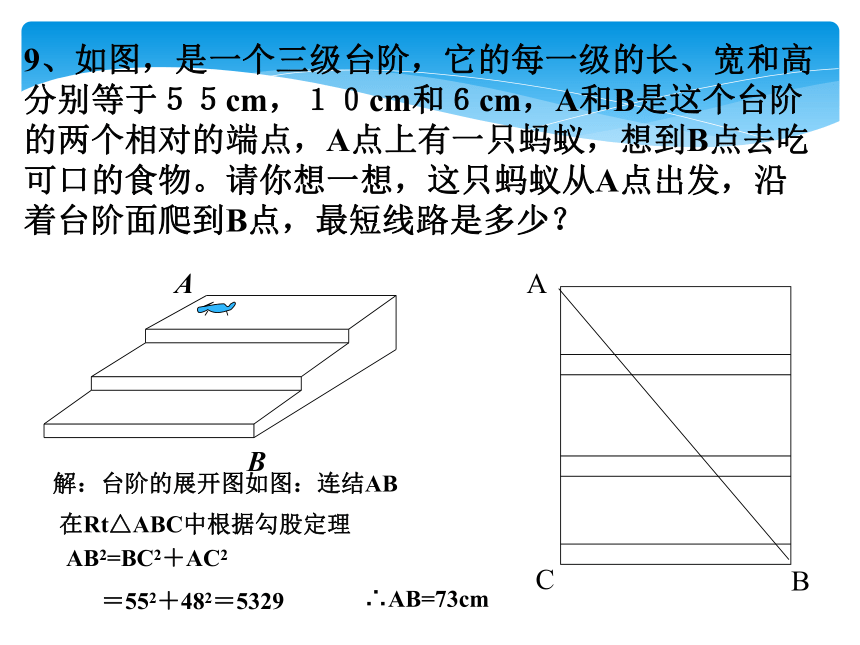
9、如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
解:台阶的展开图如图:连结AB
在Rt△ABC中根据勾股定理
AB2=BC2+AC2
=552+482=5329
∴AB=73cm
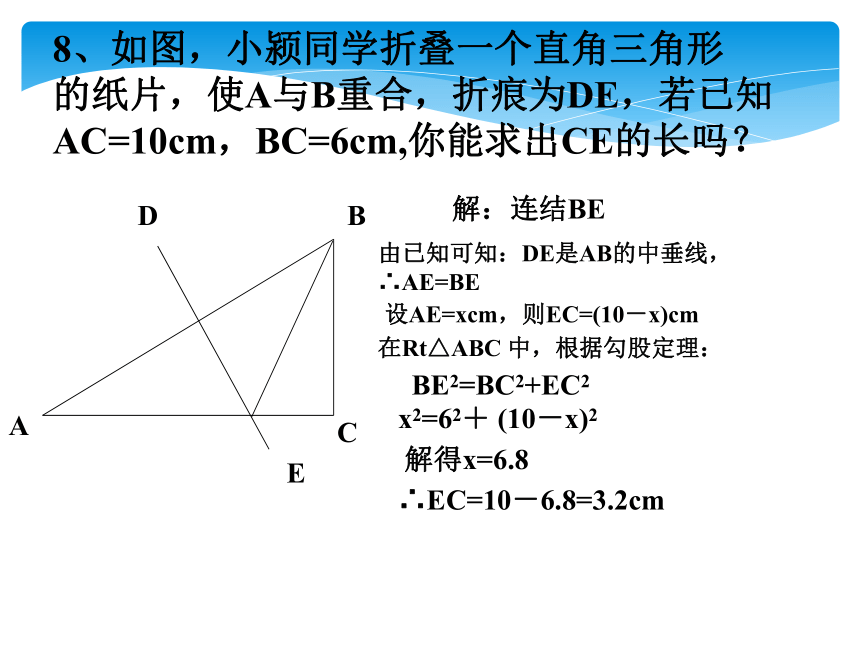
8、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
解:连结BE
由已知可知:DE是AB的中垂线,∴AE=BE
在Rt△ABC 中,根据勾股定理:
设AE=xcm,则EC=(10-x)cm
BE2=BC2+EC2
x2=62+ (10-x)2
解得x=6.8
∴EC=10-6.8=3.2cm
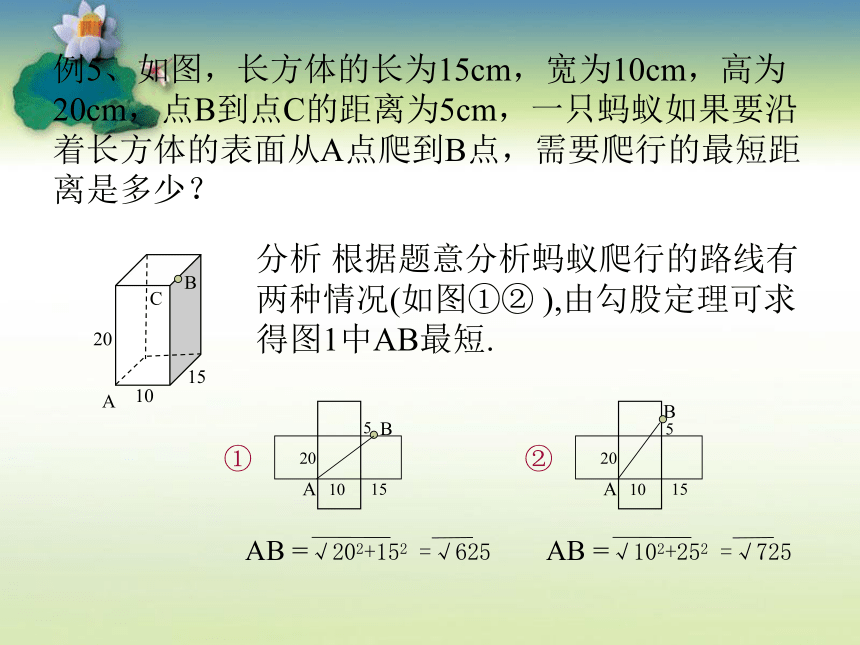
例5、如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少?
20
10
15
B
C
A
分析 根据题意分析蚂蚁爬行的路线有两种情况(如图①② ),由勾股定理可求得图1中AB最短.
①
B
A
20
10
15
5
AB =√202+152 =√625
B
AB =√102+252 =√725
②
A
20
10
15
5
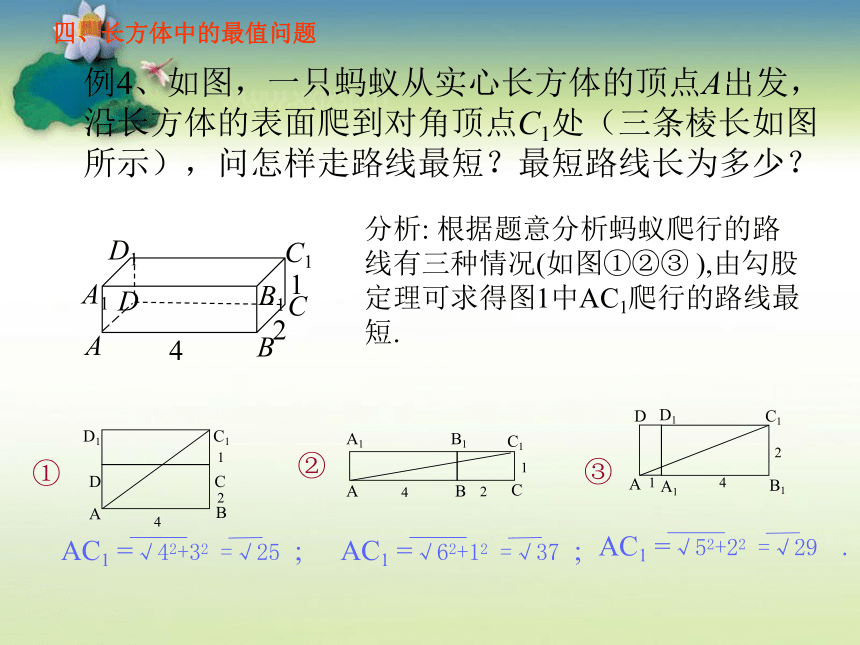
例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.
A
B
D
C
D1
C1
①
4
2
1
AC1 =√42+32 =√25 ;
②
A
B
B1
C
A1
C1
4
1
2
AC1 =√62+12 =√37 ;
A
B1
D1
D
A1
C1
③
4
1
2
AC1 =√52+22 =√29 .
四、长方体中的最值问题
二、圆柱(锥)中的最值问题
例2、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?
A
B
分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)
解:AC = 6 – 1 = 5 ,
BC = 24 × = 12,
由勾股定理得
AB2= AC2+ BC2=169,
∴AB=13(m) .
2
1
B
A
C
10、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
解:由已知AF=FC
设AF=x,则FB=9-x
在R t △ABC中,根据勾股定理FC2=FB2+BC2
则有x2=(9-x)2+32
解得x=5
同理可得DE=4
∴GF=1
∴以EF为边的正方形的面积=EG2+GF2=32+12=10
11、假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
A
B
8
2
3
6
1
C
解:过B点向南作垂线,连结AB,可得Rt△ABC
由题意可知:AC=6千米,BC=8千米
根据勾股定理AB2=AC2+BC2
=62+82=100
∴AB=10千米
11、如图,已知:CD⊥AB于D,
且有
求证:△ACB为直角三角形
A
B
D
C
9.一艘轮船以20千米/时的速度离开港口向东北方向航行,另一艘轮船同时离开港口以15千米/时的速度向东南方向航行,它们离开港口2小时后相距多少千米?
10.已知:如图,∠ABD=∠C=90°,AD=12,AC=BC,∠DAB=30°,求BC的长.
8、如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B、C 两个村庄,现要在 B、C两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园?请通过计算说明.
A
B
C
400
1000
60°
30°
D
6.在Rt△ABC中,∠C=90°,CD 是高,AB=1,则 2 CD2 + AD2 +BD2 =____;
7.三角形的三边长 a, b, c 满足
a2 +b2 +c2 +338 = 10a + 24b +26c,
此三角形为_____三角形.
5、如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
24平方米
3.以下各组数为三边的三角形中,不是直角三角形的是( ).
A. B.7,24,25
C.4,7.5,8.5 D.3.5,4.5,5.5
1.请完成以下未完成的勾股数:
(1)8、15、_______;(2)10、26、_____.
2.△ABC中,a2+b2=25,a2-b2=7,又c=5,
则最大边上的高是_______.
4.如图,两个正方形的面积分别
为64,49,则AC= .
A
D
C
64
49
17
A
B
C
A
C
P
A
C
探索与提高2:
如图所示,在△ABC中,AB=AC=4,P为BC上的一点,
(1)求证:
1、如图,在四边形ABCD中,∠BAD=90°,AD=4,AB=3,BC=12,求正方形DCEF的面积.
2、已知,如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC上任意一点,
求证:BD2+CD2=2AD2.
提升“学力”
∵AC⊥AB(已知)
∴ AC2+AB2=BC2(勾股定理)
∵ AB=3cm,BC=5cm
又∵CD=2 cm AD=2cm(已知)
∴ AC2=16 , CD2+AD2=12+4=16
∴ AC2=CD2+AD2
∴ ∠ADC=900(勾股定理的逆定理)
∴ S四边形ABCD=S △ ABC+ S△ ACD
∴
= ×3 × 4+ × 2?2
=6+2 (cm2)
= AB ?AC+ AD ?CD
解(1)
13、如图:边长为4的正方形ABCD中,F是DC的中点,
且CE= BC,则AF⊥EF,试说明理由
解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC
∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25
∴AD=4,DF=2,FC=2,EC=1
∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF
A
探索与提高:
如图所示,现在已测得长方体木块的长3厘米,宽4厘米,高24厘米。一只蜘蛛潜伏在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处。
A
C
D
B
G
F
H
(1)蜘蛛急于想捉住苍蝇,沿着长方体的表面向上爬,它要从点A爬到点B处,有无数条路线,它们有长有短,蜘蛛究竟应该沿着怎样的路线爬上去,所走的路程会最短。你能帮蜘蛛找到最短路径吗?
(2)若蜘蛛爬行的速度是每秒10厘米,问蜘蛛沿长方体表面至少爬行几秒钟,才能迅速地抓到苍蝇?
A
C
D
B
G
F
H
A
C
F
G
H
D
感悟与反思
1、通过这节课的学习活动你有哪些收获?
2、对这节课的学习,你还有什么想法吗?
试一试:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
回顾与思考
-----------勾股定理
1、直角三角形的边、角之间分别存在着什么关系?
2、请你举一个生活中的实例,并应用勾股定理解决它。
课堂练习: 一判断题. 1.?ABC的两边AB=5,AC=12,则BC=13 ( )
2.? ABC的a=6,b=8,则c=10 ( )
?
?
二填空题 1.在? ABC中,C=90°, (1)若c=10,a:b=3:4,则a=____,b=___.
(2)若a=9,b=40,则c=______. 2.在? ABC中, C=90°,若AC=6,CB=8,则?ABC面积为_____,斜边为上的高为______.
6
8
41
24
4.8
3.若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm
D
4如图,在△ABC中,AB=AC,D点在CB延长线上,求证:AD2-AB2=BD·CD
A
B
C
D
证明:
过A作AE⊥BC于E
E
∵AB=AC,∴BE=CE
在Rt △ADE中,
AD2=AE2+DE2
在Rt △ABE中,
AB2=AE2+BE2
∴ AD2-AB2=(AE2+DE2)-(AE2+BE2)
= DE2- BE2
= (DE+BE)·( DE- BE)
= (DE+CE)·( DE- BE)
=BD·CD
5、已知:数7和24,请你再写一个整数,
使这些数恰好是一个直角三角形三边的长,
则这个数可以是——
6、一个直角三角形的三边长是不大于10的三个连续偶数,则它的周长是————
25
24
7 .观察下列表格:
……
列举
猜想
3、4、5
32=4+5
5、12、13
52=12+13
7、24、25
72=24+25
……
13、b、c
132=b+c
请你结合该表格及相关知识,求出b、c的值.
即b= ,c=
84
85
9、如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
解:台阶的展开图如图:连结AB
在Rt△ABC中根据勾股定理
AB2=BC2+AC2
=552+482=5329
∴AB=73cm
8、如图,小颍同学折叠一个直角三角形
的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
解:连结BE
由已知可知:DE是AB的中垂线,∴AE=BE
在Rt△ABC 中,根据勾股定理:
设AE=xcm,则EC=(10-x)cm
BE2=BC2+EC2
x2=62+ (10-x)2
解得x=6.8
∴EC=10-6.8=3.2cm
例5、如图,长方体的长为15cm,宽为10cm,高为20cm,点B到点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从A点爬到B点,需要爬行的最短距离是多少?
20
10
15
B
C
A
分析 根据题意分析蚂蚁爬行的路线有两种情况(如图①② ),由勾股定理可求得图1中AB最短.
①
B
A
20
10
15
5
AB =√202+152 =√625
B
AB =√102+252 =√725
②
A
20
10
15
5
例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?
A
B
A1
B1
D
C
D1
C1
2
1
4
分析: 根据题意分析蚂蚁爬行的路线有三种情况(如图①②③ ),由勾股定理可求得图1中AC1爬行的路线最短.
A
B
D
C
D1
C1
①
4
2
1
AC1 =√42+32 =√25 ;
②
A
B
B1
C
A1
C1
4
1
2
AC1 =√62+12 =√37 ;
A
B1
D1
D
A1
C1
③
4
1
2
AC1 =√52+22 =√29 .
四、长方体中的最值问题
二、圆柱(锥)中的最值问题
例2、 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处
吃食物,它爬行的最短路线长为多少?
A
B
分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)
解:AC = 6 – 1 = 5 ,
BC = 24 × = 12,
由勾股定理得
AB2= AC2+ BC2=169,
∴AB=13(m) .
2
1
B
A
C
10、如图,把长方形纸片ABCD折叠,使顶点A与顶点C重合在一起,EF为折痕。若AB=9,BC=3,试求以折痕EF为边长的正方形面积。
A
B
C
D
G
F
E
解:由已知AF=FC
设AF=x,则FB=9-x
在R t △ABC中,根据勾股定理FC2=FB2+BC2
则有x2=(9-x)2+32
解得x=5
同理可得DE=4
∴GF=1
∴以EF为边的正方形的面积=EG2+GF2=32+12=10
11、假期中,王强和同学到某海岛上去玩探宝游戏,按照探宝图,他们登陆后先往东走8千米,又往北走2千米,遇到障碍后又往西走3千米,在折向北走到6千米处往东一拐,仅走1千米就找到宝藏,问登陆点A 到宝藏埋藏点B的距离是多少千米?
A
B
8
2
3
6
1
C
解:过B点向南作垂线,连结AB,可得Rt△ABC
由题意可知:AC=6千米,BC=8千米
根据勾股定理AB2=AC2+BC2
=62+82=100
∴AB=10千米
11、如图,已知:CD⊥AB于D,
且有
求证:△ACB为直角三角形
A
B
D
C
9.一艘轮船以20千米/时的速度离开港口向东北方向航行,另一艘轮船同时离开港口以15千米/时的速度向东南方向航行,它们离开港口2小时后相距多少千米?
10.已知:如图,∠ABD=∠C=90°,AD=12,AC=BC,∠DAB=30°,求BC的长.
8、如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B、C 两个村庄,现要在 B、C两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园?请通过计算说明.
A
B
C
400
1000
60°
30°
D
6.在Rt△ABC中,∠C=90°,CD 是高,AB=1,则 2 CD2 + AD2 +BD2 =____;
7.三角形的三边长 a, b, c 满足
a2 +b2 +c2 +338 = 10a + 24b +26c,
此三角形为_____三角形.
5、如图,有一块地,已知,AD=4m,
CD=3m,∠ADC=90°,AB=13m,
BC=12m。求这块地的面积。
A
B
C
3
4
13
12
D
24平方米
3.以下各组数为三边的三角形中,不是直角三角形的是( ).
A. B.7,24,25
C.4,7.5,8.5 D.3.5,4.5,5.5
1.请完成以下未完成的勾股数:
(1)8、15、_______;(2)10、26、_____.
2.△ABC中,a2+b2=25,a2-b2=7,又c=5,
则最大边上的高是_______.
4.如图,两个正方形的面积分别
为64,49,则AC= .
A
D
C
64
49
17
A
B
C
A
C
P
A
C
探索与提高2:
如图所示,在△ABC中,AB=AC=4,P为BC上的一点,
(1)求证:
1、如图,在四边形ABCD中,∠BAD=90°,AD=4,AB=3,BC=12,求正方形DCEF的面积.
2、已知,如图,Rt△ABC中,∠BAC=90°,AB=AC,D是BC上任意一点,
求证:BD2+CD2=2AD2.
提升“学力”
∵AC⊥AB(已知)
∴ AC2+AB2=BC2(勾股定理)
∵ AB=3cm,BC=5cm
又∵CD=2 cm AD=2cm(已知)
∴ AC2=16 , CD2+AD2=12+4=16
∴ AC2=CD2+AD2
∴ ∠ADC=900(勾股定理的逆定理)
∴ S四边形ABCD=S △ ABC+ S△ ACD
∴
= ×3 × 4+ × 2?2
=6+2 (cm2)
= AB ?AC+ AD ?CD
解(1)
13、如图:边长为4的正方形ABCD中,F是DC的中点,
且CE= BC,则AF⊥EF,试说明理由
解:连接AE
∵ABCD是正方形,边长是4,F是DC的中点,EC=1/4BC
∴根据勾股定理,在
Rt△ADF,AF2=AD2+DF2=20
Rt△EFC,EF2=EC2+FC2=5
Rt△ABE,AE2=AB2+BE2=25
∴AD=4,DF=2,FC=2,EC=1
∴AE2=EF2+AF2 ∴∠AEF=90°即AF ⊥EF
A
探索与提高:
如图所示,现在已测得长方体木块的长3厘米,宽4厘米,高24厘米。一只蜘蛛潜伏在木块的一个顶点A处,一只苍蝇在这个长方体上和蜘蛛相对的顶点B处。
A
C
D
B
G
F
H
(1)蜘蛛急于想捉住苍蝇,沿着长方体的表面向上爬,它要从点A爬到点B处,有无数条路线,它们有长有短,蜘蛛究竟应该沿着怎样的路线爬上去,所走的路程会最短。你能帮蜘蛛找到最短路径吗?
(2)若蜘蛛爬行的速度是每秒10厘米,问蜘蛛沿长方体表面至少爬行几秒钟,才能迅速地抓到苍蝇?
A
C
D
B
G
F
H
A
C
F
G
H
D
感悟与反思
1、通过这节课的学习活动你有哪些收获?
2、对这节课的学习,你还有什么想法吗?
试一试:
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?
D
A
B
C
