人教版八年级下册18.2.2菱形的判定课件(第二课时 18张)
文档属性
| 名称 | 人教版八年级下册18.2.2菱形的判定课件(第二课时 18张) |  | |
| 格式 | pptx | ||
| 文件大小 | 124.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 10:39:38 | ||
图片预览




文档简介
人教版八年级数学
菱 形
第2课时 菱形的判定
课标解读
1.理解菱形的定义,能够利用定义法判定四边形是菱形。
2.掌握菱形的判定定理,并能灵活运用菱形的判定定理进行菱形的判定。
3.掌握各种判定方法的特点,能够根据题中特点选择一个恰当的方法。
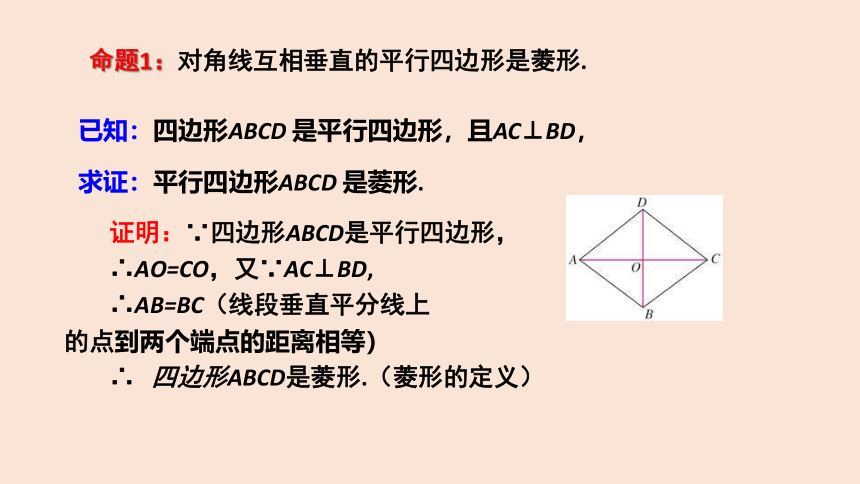
命题1:对角线互相垂直的平行四边形是菱形.
已知:四边形ABCD 是平行四边形,且AC⊥BD,
求证:平行四边形ABCD 是菱形.
证明:∵四边形ABCD是平行四边形,
∴AO=CO,又∵AC⊥BD,
∴AB=BC(线段垂直平分线上
的点到两个端点的距离相等)
∴ 四边形ABCD是菱形.(菱形的定义)
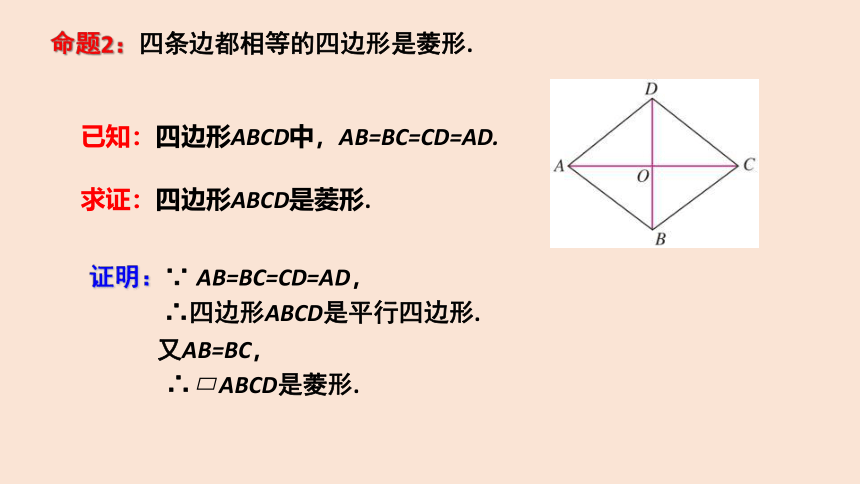
命题2:四条边都相等的四边形是菱形.
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:∵ AB=BC=CD=AD,
∴四边形ABCD是平行四边形.
又AB=BC,
∴ ABCD是菱形.
菱形的判定定理
(1)有一组________相等的平行四边形是菱形;
(2)________条边相等的四边形是菱形;
(3)对角线__________的平行四边形是菱形;
(4)对角线互相垂直且平分的四边形是菱形.(证明过程中不能直接应用,可转换到判定(3))
邻边
四
互相垂直
四边形
+
四条边相等
菱形
归纳总结
四边形
+
对角线垂直平分
菱形
平行四边形
+
一组邻边相等
菱形
平行四边形
+
对角线垂直
菱形
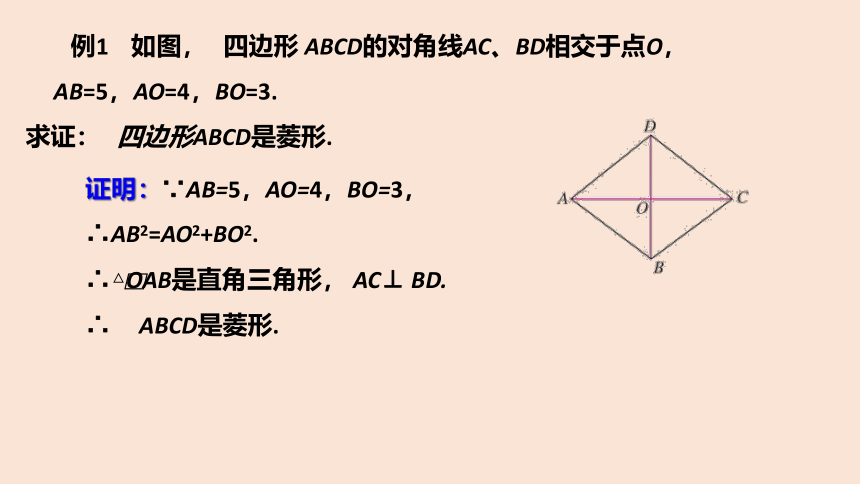
例1 如图, 四边形 ABCD的对角线AC、BD相交于点O,
AB=5,AO=4,BO=3.
求证: 四边形ABCD是菱形.
证明:∵AB=5,AO=4,BO=3,
∴AB2=AO2+BO2.
∴△OAB是直角三角形, AC⊥ BD.
∴ ABCD是菱形.
例2.如图,AE∥BF,AC平分∠BAD,且交BF于点C,BO平分∠ABC,且交AE于点D,连接CD,求证:四边形ABCD是菱形.
证明:∵AE∥BF,∴∠EAC=∠ACB.
又∵AC平分∠BAD,
∴∠ACB=∠BAC=∠EAC,∴AB=BC.
同理:AB=AD,∴AD=BC,而AD∥BC.
∴四边形ABCD是平行四边形.又AB=AD,
∴平行四边形ABCD是菱形.
1. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AB=5,OA=4,OB=3.
求证:四边形ABCD是菱形.
证明:∵AB=5,OA=4,OB=3,
∴AB2=AO2+BO2,
∴△ABO为直角三角形,
∴______________,
∵四边形ABCD为平行四边形,
∴四边形ABCD为菱形.
(依据:___________________________________)
AC⊥BD
对角线互相垂直的平行四边形是菱形
同步练习
2. 如图所示,下列条件中能说明四边形ABCD是菱形的有( )
②OA=OC,OB=OD,AB=BC;
①BD⊥AC
③AC=BD,
④AB=BC,AB∥CD
A.① B. ① ② C. ② D ③④
C
A
B
C
D
O
3.(2019·宁夏)如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD B.AB=AD
C.AC=BD D.∠ABD=∠CBD
C
如图,已知四边形ABCD,对角线AC、BD交于点O.现给出四个条件:①AC⊥BD;②AC平分BD;③AD∥BC;④∠OAD=∠ODA.
请你以其中的三个作为题设,以“四边形ABCD是菱形”作为结论.
(1)写出一个真命题,并证明;
(2)写出一个假命题,并举出一个反例加以说明.
拓展提升
解:(1)若①②③,则四边形ABCD是菱形.
∵AC⊥BD,AC平分BD,
∴∠BOC=∠DOA=90°,BO=OD.
又∵AD∥BC,∴∠OBC=∠ODA.
∴△BOC≌△DOA,∴OC=OA.
∴AC、BD互相垂直且平分,
∴四边形ABCD是菱形.
(2)若②③④,则四边形ABCD是菱形.
反例:当四边形ABCD是矩形时,满足②③④,但不是菱形.
2.一个平行四边形的一条边长是9,两条对角线的长分别是12和6 ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
解:这是一个菱形.
AO=CO= AC=6,
BO=DO= BD=3 .
在△ABO中,∵AO2+BO2=(3 )2+62=81,
AB2=92=81,∴△ABO是直角三角形,
∴AC⊥BD,∴ ABCD是菱形.
S菱形ABCD= AC · BD
=36
3. 如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BOC=120°,AB=4,求△BEC的面积.
解: (1)证明:∵CE∥BD,DE∥AC,
∴四边形OCED是平行四边形,
∵矩形ABCD的对角线AC,BD相交于点O,
∴OC=1/2AC,OD=1/2BD,AC=BD.
∴OC=OD.
∴四边形OCED是菱形;
(2)解:∵∠BOC=120°,∴∠DOC=60°.
∵四边形OCED是菱形,∴△ODC,△CDE是等边三角形.
∴OC=DC.
∵OC=1/2AC,∴AC=2OC=2CD.
∵四边形ABCD是矩形,∴AB=CD.
∴AC=2AB.
∵AB=4,∴AC=8.
在Rt△ABC中,BC==4.
如解图,过点E作EF⊥CD,可得CF=2(1)CD=2.
∴S△BEC=1/2BC×CF=4.
菱 形
第2课时 菱形的判定
课标解读
1.理解菱形的定义,能够利用定义法判定四边形是菱形。
2.掌握菱形的判定定理,并能灵活运用菱形的判定定理进行菱形的判定。
3.掌握各种判定方法的特点,能够根据题中特点选择一个恰当的方法。
命题1:对角线互相垂直的平行四边形是菱形.
已知:四边形ABCD 是平行四边形,且AC⊥BD,
求证:平行四边形ABCD 是菱形.
证明:∵四边形ABCD是平行四边形,
∴AO=CO,又∵AC⊥BD,
∴AB=BC(线段垂直平分线上
的点到两个端点的距离相等)
∴ 四边形ABCD是菱形.(菱形的定义)
命题2:四条边都相等的四边形是菱形.
已知:四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.
证明:∵ AB=BC=CD=AD,
∴四边形ABCD是平行四边形.
又AB=BC,
∴ ABCD是菱形.
菱形的判定定理
(1)有一组________相等的平行四边形是菱形;
(2)________条边相等的四边形是菱形;
(3)对角线__________的平行四边形是菱形;
(4)对角线互相垂直且平分的四边形是菱形.(证明过程中不能直接应用,可转换到判定(3))
邻边
四
互相垂直
四边形
+
四条边相等
菱形
归纳总结
四边形
+
对角线垂直平分
菱形
平行四边形
+
一组邻边相等
菱形
平行四边形
+
对角线垂直
菱形
例1 如图, 四边形 ABCD的对角线AC、BD相交于点O,
AB=5,AO=4,BO=3.
求证: 四边形ABCD是菱形.
证明:∵AB=5,AO=4,BO=3,
∴AB2=AO2+BO2.
∴△OAB是直角三角形, AC⊥ BD.
∴ ABCD是菱形.
例2.如图,AE∥BF,AC平分∠BAD,且交BF于点C,BO平分∠ABC,且交AE于点D,连接CD,求证:四边形ABCD是菱形.
证明:∵AE∥BF,∴∠EAC=∠ACB.
又∵AC平分∠BAD,
∴∠ACB=∠BAC=∠EAC,∴AB=BC.
同理:AB=AD,∴AD=BC,而AD∥BC.
∴四边形ABCD是平行四边形.又AB=AD,
∴平行四边形ABCD是菱形.
1. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,AB=5,OA=4,OB=3.
求证:四边形ABCD是菱形.
证明:∵AB=5,OA=4,OB=3,
∴AB2=AO2+BO2,
∴△ABO为直角三角形,
∴______________,
∵四边形ABCD为平行四边形,
∴四边形ABCD为菱形.
(依据:___________________________________)
AC⊥BD
对角线互相垂直的平行四边形是菱形
同步练习
2. 如图所示,下列条件中能说明四边形ABCD是菱形的有( )
②OA=OC,OB=OD,AB=BC;
①BD⊥AC
③AC=BD,
④AB=BC,AB∥CD
A.① B. ① ② C. ② D ③④
C
A
B
C
D
O
3.(2019·宁夏)如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD B.AB=AD
C.AC=BD D.∠ABD=∠CBD
C
如图,已知四边形ABCD,对角线AC、BD交于点O.现给出四个条件:①AC⊥BD;②AC平分BD;③AD∥BC;④∠OAD=∠ODA.
请你以其中的三个作为题设,以“四边形ABCD是菱形”作为结论.
(1)写出一个真命题,并证明;
(2)写出一个假命题,并举出一个反例加以说明.
拓展提升
解:(1)若①②③,则四边形ABCD是菱形.
∵AC⊥BD,AC平分BD,
∴∠BOC=∠DOA=90°,BO=OD.
又∵AD∥BC,∴∠OBC=∠ODA.
∴△BOC≌△DOA,∴OC=OA.
∴AC、BD互相垂直且平分,
∴四边形ABCD是菱形.
(2)若②③④,则四边形ABCD是菱形.
反例:当四边形ABCD是矩形时,满足②③④,但不是菱形.
2.一个平行四边形的一条边长是9,两条对角线的长分别是12和6 ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
解:这是一个菱形.
AO=CO= AC=6,
BO=DO= BD=3 .
在△ABO中,∵AO2+BO2=(3 )2+62=81,
AB2=92=81,∴△ABO是直角三角形,
∴AC⊥BD,∴ ABCD是菱形.
S菱形ABCD= AC · BD
=36
3. 如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BOC=120°,AB=4,求△BEC的面积.
解: (1)证明:∵CE∥BD,DE∥AC,
∴四边形OCED是平行四边形,
∵矩形ABCD的对角线AC,BD相交于点O,
∴OC=1/2AC,OD=1/2BD,AC=BD.
∴OC=OD.
∴四边形OCED是菱形;
(2)解:∵∠BOC=120°,∴∠DOC=60°.
∵四边形OCED是菱形,∴△ODC,△CDE是等边三角形.
∴OC=DC.
∵OC=1/2AC,∴AC=2OC=2CD.
∵四边形ABCD是矩形,∴AB=CD.
∴AC=2AB.
∵AB=4,∴AC=8.
在Rt△ABC中,BC==4.
如解图,过点E作EF⊥CD,可得CF=2(1)CD=2.
∴S△BEC=1/2BC×CF=4.
