人教版九年级上册 数学24.4.1弧长和扇形面积 课件(23张)
文档属性
| 名称 | 人教版九年级上册 数学24.4.1弧长和扇形面积 课件(23张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 10:40:19 | ||
图片预览






文档简介
在田径二百米跑比赛中,每位运动员的起跑位置相同吗?每位运动员弯路的展直长度相同吗?
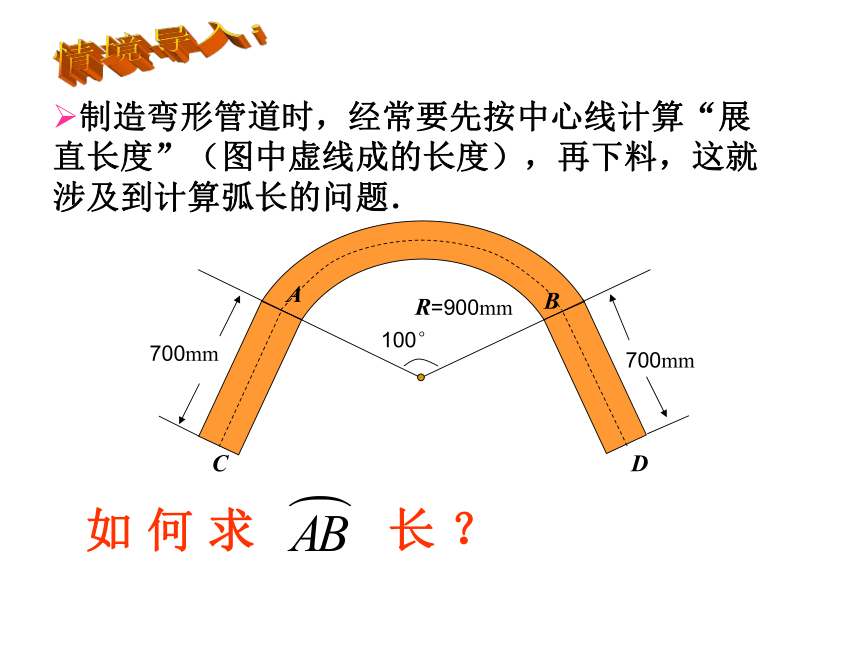
制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线成的长度),再下料,这就涉及到计算弧长的问题.
如 何 求 长 ?
700mm
R=900mm
700mm
100°
A
B
C
D
4. n°的圆心角呢?
半径为R圆的周长为
可以看作是360°圆心角所对的弧长
1°的圆心角所对弧长是
n°的圆心角所对的弧长
1. 你还记得圆周长的计算公式吗?
2. 圆的周长可以看作是多少度的圆 心角所对的弧长?
3. 1°的圆心角所对弧长是多少?
R
·
n°
1°
O
想一想
n°
A
B
O
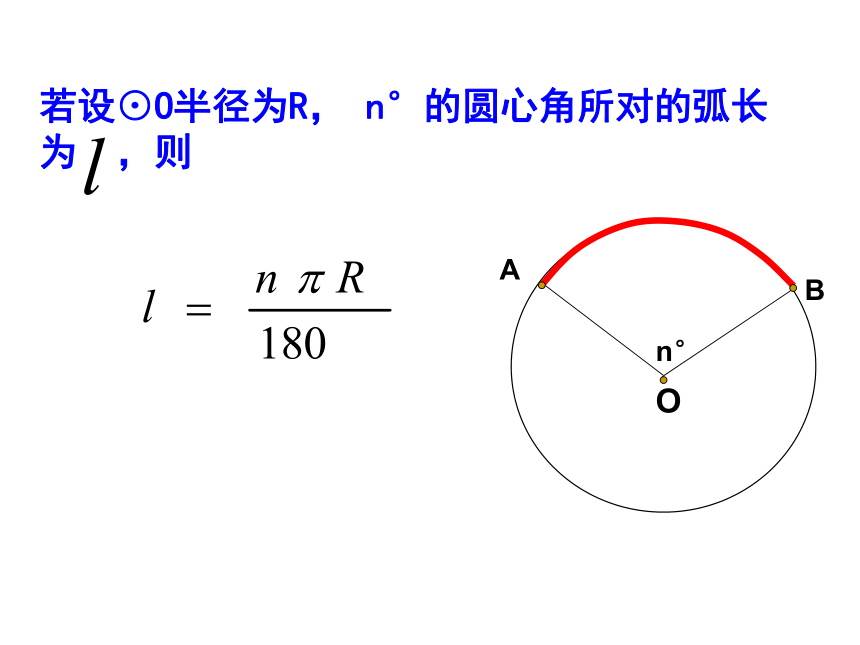
若设⊙O半径为R, n°的圆心角所对的弧长为 ,则
例:
已知圆弧的半径为50厘米,圆心角为60°,
求此圆弧的长度。
=
(cm)
答:此圆弧的长度为
cm
解:
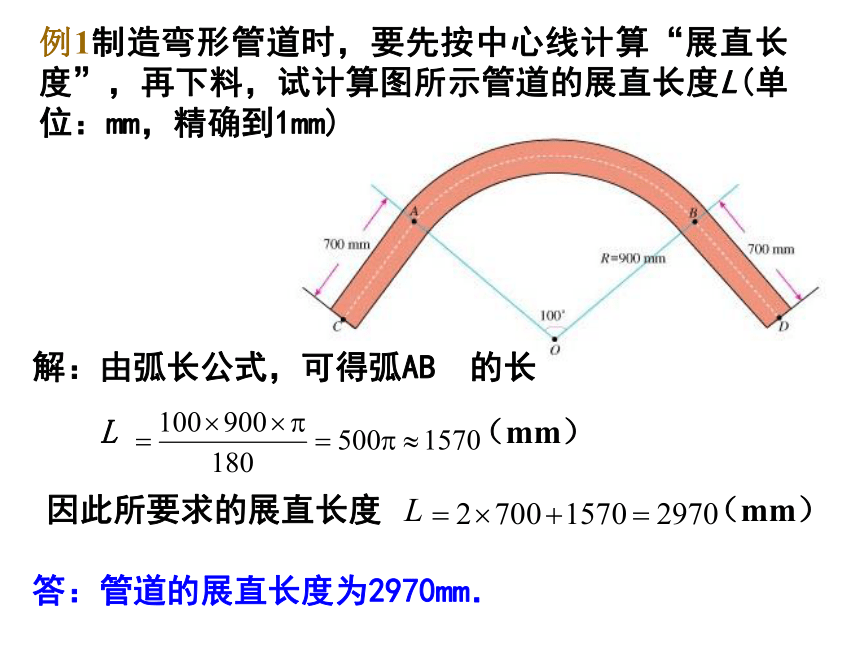
例1制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
L (mm)
因此所要求的展直长度
L (mm)
答:管道的展直长度为2970mm.
1.已知弧所对的圆心角为90°,半径是4,则弧长为____。
2. (06·随州)已知一条弧的半径为9,弧长为8π ,那么这条弧所对的圆心角为____。
3. (06·枣庄)钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D.
小试牛刀
4、有一段弯道是圆弧形的,道长是12m,弧所对的圆心角是81o,求这段圆弧的半径R(精确到0.1m).
如图,由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形,
·
O
A
B
n°
R
想一想
可以发现,扇形面积与组成扇形的圆心角的大小有关,圆心角越大,扇形面积也就越大.
从 练习 中 悟 方 法
3. 1°的圆心角所对的扇形面积是多少?
1. 你还记得圆面积公式吗?
2. 圆面积可以看作是多少度的圆心角所对的扇形的面积?
4. n°的圆心角呢?
圆的面积公式:
360°的圆心角所对的扇形的面积.
R
·
n°
1°
O
想一想 怎样计算圆半径为R,圆心角为n°的扇形面积呢?
1°的圆心角所对的扇形面积是
圆心角为n°的扇形面积是
思考:扇形的面积公式与弧长公式有联系吗?
如果扇形的半径为R的圆中,圆心角为no ,那么扇形面积的计算公式为:
扇形的弧长与扇形面积的关系为:
想一想:扇形的面积公式与什么公式类似?
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
随堂训练
1、已知扇形的圆心角为120°,半径为2,则这个
扇形的面积S扇形=____.
2、已知扇形面积为 ,圆心角为60°,则这个
扇形的半径R=____.
3、已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积是_________.
例2 如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积(精确到0.01m2).
A
B
C
D
O
解:如图,连接OA、OB,作弦
AB的垂直平分线,垂足为D,交
于点C.
例题讲解
∵OC=0.6,DC=0.3,
∴OD=OC-DC=0.3.
在Rt△OAD中,OA=0.6,利用勾股定理可得,
有水部分的面积
例题讲解
A
B
C
D
O
∴∠OAD=30°
∴ ∠AOD=60 °,∠AOB=120°
在Rt△AOD中,
练习:如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
变式训练
S弓形= S扇形+S△
感悟:
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△
如图,正三角形ABC的边长为a,分别以A、B、 C 为圆心,以 为半径的圆相切于点D、E、F,求图中阴影部分的面积.
A
B
C
F
E
D
解:连接AD,则
垂足为D
根据勾股定理,得
练一练(书P113 第3题)
又知,S扇形BDF=S扇形CDE=S扇形AEF,
练一练
A
B
C
F
E
D
随堂训练
4、如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为120°,OC
长为8cm,CA长为12
cm,则贴纸部分的面
积为( )
A. B.
C. D.
5.课本P115【习题24.4】第1题(1)、(2)
探究题:如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求图中阴影部分的面积。
试金石
一、弧长的计算公式
三、扇形面积计算公式
二、扇形的概念
制造弯形管道时,经常要先按中心线计算“展直长度”(图中虚线成的长度),再下料,这就涉及到计算弧长的问题.
如 何 求 长 ?
700mm
R=900mm
700mm
100°
A
B
C
D
4. n°的圆心角呢?
半径为R圆的周长为
可以看作是360°圆心角所对的弧长
1°的圆心角所对弧长是
n°的圆心角所对的弧长
1. 你还记得圆周长的计算公式吗?
2. 圆的周长可以看作是多少度的圆 心角所对的弧长?
3. 1°的圆心角所对弧长是多少?
R
·
n°
1°
O
想一想
n°
A
B
O
若设⊙O半径为R, n°的圆心角所对的弧长为 ,则
例:
已知圆弧的半径为50厘米,圆心角为60°,
求此圆弧的长度。
=
(cm)
答:此圆弧的长度为
cm
解:
例1制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度L(单位:mm,精确到1mm)
解:由弧长公式,可得弧AB 的长
L (mm)
因此所要求的展直长度
L (mm)
答:管道的展直长度为2970mm.
1.已知弧所对的圆心角为90°,半径是4,则弧长为____。
2. (06·随州)已知一条弧的半径为9,弧长为8π ,那么这条弧所对的圆心角为____。
3. (06·枣庄)钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D.
小试牛刀
4、有一段弯道是圆弧形的,道长是12m,弧所对的圆心角是81o,求这段圆弧的半径R(精确到0.1m).
如图,由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形,
·
O
A
B
n°
R
想一想
可以发现,扇形面积与组成扇形的圆心角的大小有关,圆心角越大,扇形面积也就越大.
从 练习 中 悟 方 法
3. 1°的圆心角所对的扇形面积是多少?
1. 你还记得圆面积公式吗?
2. 圆面积可以看作是多少度的圆心角所对的扇形的面积?
4. n°的圆心角呢?
圆的面积公式:
360°的圆心角所对的扇形的面积.
R
·
n°
1°
O
想一想 怎样计算圆半径为R,圆心角为n°的扇形面积呢?
1°的圆心角所对的扇形面积是
圆心角为n°的扇形面积是
思考:扇形的面积公式与弧长公式有联系吗?
如果扇形的半径为R的圆中,圆心角为no ,那么扇形面积的计算公式为:
扇形的弧长与扇形面积的关系为:
想一想:扇形的面积公式与什么公式类似?
A
B
O
O
比较扇形面积与弧长公式, 用弧长表示扇形面积:
随堂训练
1、已知扇形的圆心角为120°,半径为2,则这个
扇形的面积S扇形=____.
2、已知扇形面积为 ,圆心角为60°,则这个
扇形的半径R=____.
3、已知半径为2cm的扇形,其弧长为 ,
则这个扇形的面积是_________.
例2 如图,水平放置的圆柱形排水管道的截面半径是0.6m,其中水面高0.3m,求截面上有水部分的面积(精确到0.01m2).
A
B
C
D
O
解:如图,连接OA、OB,作弦
AB的垂直平分线,垂足为D,交
于点C.
例题讲解
∵OC=0.6,DC=0.3,
∴OD=OC-DC=0.3.
在Rt△OAD中,OA=0.6,利用勾股定理可得,
有水部分的面积
例题讲解
A
B
C
D
O
∴∠OAD=30°
∴ ∠AOD=60 °,∠AOB=120°
在Rt△AOD中,
练习:如图,水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积。
0
A
B
D
C
E
变式训练
S弓形= S扇形+S△
感悟:
①当弓形面积小于半圆时
S弓形= S扇形-S△
②当弓形面积大于半圆时
S弓形= S扇形+S△
如图,正三角形ABC的边长为a,分别以A、B、 C 为圆心,以 为半径的圆相切于点D、E、F,求图中阴影部分的面积.
A
B
C
F
E
D
解:连接AD,则
垂足为D
根据勾股定理,得
练一练(书P113 第3题)
又知,S扇形BDF=S扇形CDE=S扇形AEF,
练一练
A
B
C
F
E
D
随堂训练
4、如图,这是中央电视台“曲苑杂谈”中的一副图案,它是一扇形图形,其中∠AOB为120°,OC
长为8cm,CA长为12
cm,则贴纸部分的面
积为( )
A. B.
C. D.
5.课本P115【习题24.4】第1题(1)、(2)
探究题:如图,⊙A、 ⊙B、 ⊙C、 ⊙D两两不相交,且半径都是2cm,求图中阴影部分的面积。
试金石
一、弧长的计算公式
三、扇形面积计算公式
二、扇形的概念
同课章节目录
