人教版九年级上册数学课件:25.1随机事件与概率(19张)
文档属性
| 名称 | 人教版九年级上册数学课件:25.1随机事件与概率(19张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览






文档简介
天有不测风云
小晨掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有1到6的点数。请考虑以下问题,掷一次骰子,在骰子向上的一面上,
(1)可能出现哪些点数?
(2)出现的点数大于0吗?
(3)出现的点数会是7吗?
(4)出现的点数会是4吗?
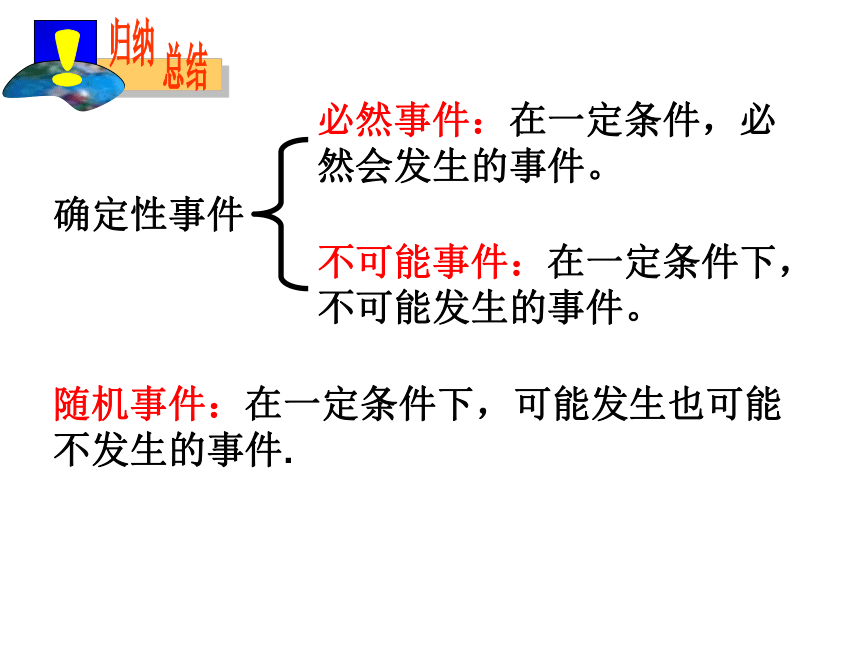
必然事件:在一定条件,必然会发生的事件。
不可能事件:在一定条件下,不可能发生的事件。
随机事件:在一定条件下,可能发生也可能不发生的事件.
确定性事件
例1 5名同学参加英语课本剧比赛,以抽签方式决定每个人的出场顺序。签筒中有5根形状、大小相同的纸签,上面分别标有出场的序号1,2,3,4,5。小军首先抽签,他在看不到纸签上的数字的情况从签筒中随机(任意)地取一根纸签。请指出下列事件中,哪些是随机事件,哪些是必然事件,哪些是不可能事件。
(2)抽到的序号是0;
(1)抽到的序号小于6;
(3)抽到的序号是1。
⑴通常加热到100°C时,水沸腾;
(2)球队员在罚球线上投篮一次,未投中;
⑶掷一个骰子,向上的一面是6点;
⑷度量三角形的内角和,结果是360°;
(5)经过城市中某一有交通信号灯的路口,遇到红灯;
(6)某射击运动员射击一次,命中靶心.
(不可能事件)
(必然事件)
(随机事件)
(随机事件)
(随机事件)
练习:
1.指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件.
(随机事件)
2.你能列举一些生活中的随机事件、不可能事件和必然事件的例子吗?
1.下列成语反映的事件是什么事件?
(1)水中捞月 (2)一箭双雕
(3)刻舟求剑 (4)守株待兔
(5)拔苗助长 (6)瓮中捉鳖
我思我进步
袋子中装有4个黑球2个白球,这些球的形状、大小、质地等完全相同。小婷在看不到球的条件下,随机地从袋子中摸出一个球。请考虑一下问题:
(1)这个球是白球还是黑球?
(2)如果两种球都有可能被摸出,那么摸出黑球和摸出白球的可能性一样大吗?
归纳:一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同。
能否通过改变袋子中某种颜色的球的数量,使“摸出黑球”和“摸出白球”的可能性大小相同?
从分别标有1,2,3,4,5号的5根纸签中随机地抽取一根,请考虑以下问题:
(1)抽出的签上的号码有几种可能?
(2)每个号被抽到的可能性大小相同吗? 是全部可能结果总数的多少?
以上游戏有什么特点吗?
可以发现以上游戏有两个特点:
(1)每一次试验中,可能出现的结果只有有限个;
(2)每一次试验中,各种结果出现的可能性相等。
概率的定义:
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记作P(A)。
归纳:
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率
P(A)=
在上述类型的试验中,通过对试验结果以及事件本身的分析,我们就可以求出相应事件的概率,在P(A)= 中,由m和n的含义可知0≤m≤n,进而 0≤m/n≤1。因此
0≤P(A) ≤1.
特别地:
当A为必然事件时,P(A)=1;
当A为不可能事件时,P(A)=0
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能发生
必然发生
概率的值
事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0。
例1 掷一个骰子,观察向上的一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于5。
练习 如图是一个转盘,转盘分成6个相同的扇形,颜色分为红、绿、黄三种颜色。指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形)。求下列事件的概率:
(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色。
把这个例中的(1)(3)两问及答案联系起来,你有什么发现?
想一想,本节课你有哪些收获?
一休得罪了幕府将军,将军决定处罚一休,幸得安国寺长老和百姓们的求情,将军终于同意让一休自己来决定自己的命运.
方法是将军写下两张签,一张罚,一张免,让一休抽签,抽中罚则罚,抽中免则免。
将军一心想处罚一休,将军会在写签时怎么写呢?原来将军在两张签上都写上了“罚”。一休不论抽到哪一张都一样要罚。
爱动脑筋的一休早就料到了这一点。一休会用什么办法应对狡诈的幕府将军呢?
罚
免
小晨掷一个质地均匀的正方形骰子,骰子的六个面上分别刻有1到6的点数。请考虑以下问题,掷一次骰子,在骰子向上的一面上,
(1)可能出现哪些点数?
(2)出现的点数大于0吗?
(3)出现的点数会是7吗?
(4)出现的点数会是4吗?
必然事件:在一定条件,必然会发生的事件。
不可能事件:在一定条件下,不可能发生的事件。
随机事件:在一定条件下,可能发生也可能不发生的事件.
确定性事件
例1 5名同学参加英语课本剧比赛,以抽签方式决定每个人的出场顺序。签筒中有5根形状、大小相同的纸签,上面分别标有出场的序号1,2,3,4,5。小军首先抽签,他在看不到纸签上的数字的情况从签筒中随机(任意)地取一根纸签。请指出下列事件中,哪些是随机事件,哪些是必然事件,哪些是不可能事件。
(2)抽到的序号是0;
(1)抽到的序号小于6;
(3)抽到的序号是1。
⑴通常加热到100°C时,水沸腾;
(2)球队员在罚球线上投篮一次,未投中;
⑶掷一个骰子,向上的一面是6点;
⑷度量三角形的内角和,结果是360°;
(5)经过城市中某一有交通信号灯的路口,遇到红灯;
(6)某射击运动员射击一次,命中靶心.
(不可能事件)
(必然事件)
(随机事件)
(随机事件)
(随机事件)
练习:
1.指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件.
(随机事件)
2.你能列举一些生活中的随机事件、不可能事件和必然事件的例子吗?
1.下列成语反映的事件是什么事件?
(1)水中捞月 (2)一箭双雕
(3)刻舟求剑 (4)守株待兔
(5)拔苗助长 (6)瓮中捉鳖
我思我进步
袋子中装有4个黑球2个白球,这些球的形状、大小、质地等完全相同。小婷在看不到球的条件下,随机地从袋子中摸出一个球。请考虑一下问题:
(1)这个球是白球还是黑球?
(2)如果两种球都有可能被摸出,那么摸出黑球和摸出白球的可能性一样大吗?
归纳:一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同。
能否通过改变袋子中某种颜色的球的数量,使“摸出黑球”和“摸出白球”的可能性大小相同?
从分别标有1,2,3,4,5号的5根纸签中随机地抽取一根,请考虑以下问题:
(1)抽出的签上的号码有几种可能?
(2)每个号被抽到的可能性大小相同吗? 是全部可能结果总数的多少?
以上游戏有什么特点吗?
可以发现以上游戏有两个特点:
(1)每一次试验中,可能出现的结果只有有限个;
(2)每一次试验中,各种结果出现的可能性相等。
概率的定义:
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A发生的概率,记作P(A)。
归纳:
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率
P(A)=
在上述类型的试验中,通过对试验结果以及事件本身的分析,我们就可以求出相应事件的概率,在P(A)= 中,由m和n的含义可知0≤m≤n,进而 0≤m/n≤1。因此
0≤P(A) ≤1.
特别地:
当A为必然事件时,P(A)=1;
当A为不可能事件时,P(A)=0
0
1
事件发生的可能性越来越大
事件发生的可能性越来越小
不可能发生
必然发生
概率的值
事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0。
例1 掷一个骰子,观察向上的一面的点数,求下列事件的概率:
(1)点数为2;
(2)点数为奇数;
(3)点数大于2且小于5。
练习 如图是一个转盘,转盘分成6个相同的扇形,颜色分为红、绿、黄三种颜色。指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形)。求下列事件的概率:
(1)指针指向红色;
(2)指针指向红色或黄色;
(3)指针不指向红色。
把这个例中的(1)(3)两问及答案联系起来,你有什么发现?
想一想,本节课你有哪些收获?
一休得罪了幕府将军,将军决定处罚一休,幸得安国寺长老和百姓们的求情,将军终于同意让一休自己来决定自己的命运.
方法是将军写下两张签,一张罚,一张免,让一休抽签,抽中罚则罚,抽中免则免。
将军一心想处罚一休,将军会在写签时怎么写呢?原来将军在两张签上都写上了“罚”。一休不论抽到哪一张都一样要罚。
爱动脑筋的一休早就料到了这一点。一休会用什么办法应对狡诈的幕府将军呢?
罚
免
同课章节目录
