人教版七年级数学4.2.2直线 射线 线段 课件(共22张ppt)
文档属性
| 名称 | 人教版七年级数学4.2.2直线 射线 线段 课件(共22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览





文档简介
线段、射线、直线的本质区别
是_____没有端点,_____只有
一个端点,_____有两个端点。
直线
线段
射线
直线的基本性质是:
____________________。
经过两点有且只有一条直线
线段、射线、直线中____可以
度量长度,所以只有____才可
以比较长短。
线段
线段
A
B
为什么有些人在A点要到马路对面B点时,不走人行横道呢?
情境1:
为什么有些人在A点要到马路对面B点时,不走人行横道呢?
情境1:
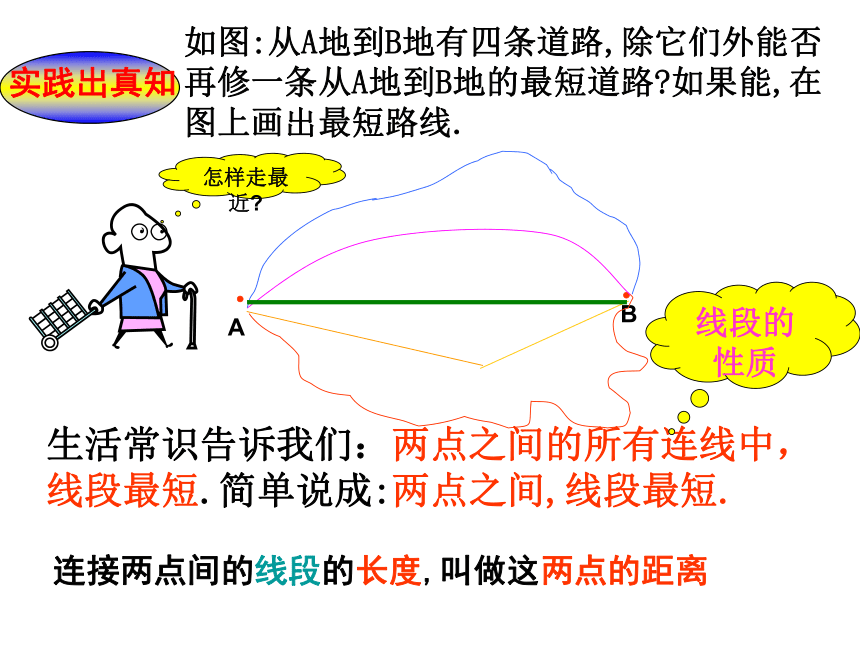
如图:从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,在图上画出最短路线.
?
?
A
B
怎样走最近?
生活常识告诉我们:两点之间的所有连线中,线段最短.简单说成:两点之间,线段最短.
线段的性质
实践出真知
连接两点间的线段的长度,叫做这两点的距离
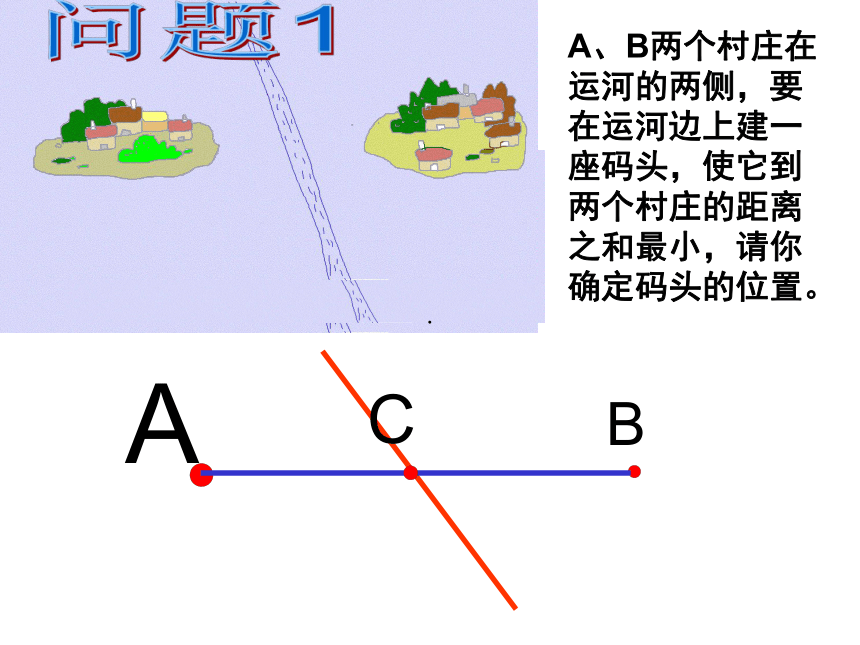
A、B两个村庄在运河的两侧,要在运河边上建一座码头,使它到两个村庄的距离之和最小,请你确定码头的位置。
·
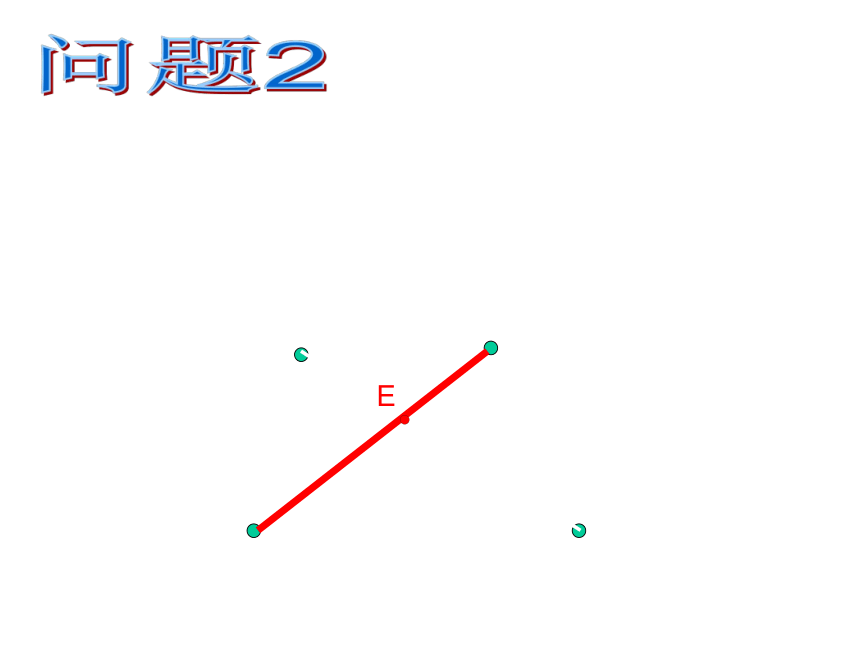
有四个居民小区,位置如图所示,若要建一个超市,使得超市到四个居民小区的距离之和最小,这个超市应建在何处?
A
B
C
D
问题征答
判断:
1.过A、B两点的直线长是A、B两点间的距离( )
2.两点间的连线的长度,叫做两点间的距离( )
3.两点之间的距离是指两点之间的线段 ( )
4. 连结A、B两点的所有线中,其中最短的线的长度
就是A、B两点间的距离( )
5.两点间的距离是连结两点的线段的长度。( )
错
错
错
对
对
如何比较两个人的身高?
从中你得到什么启发来比较
两条线段的长短?
情境2
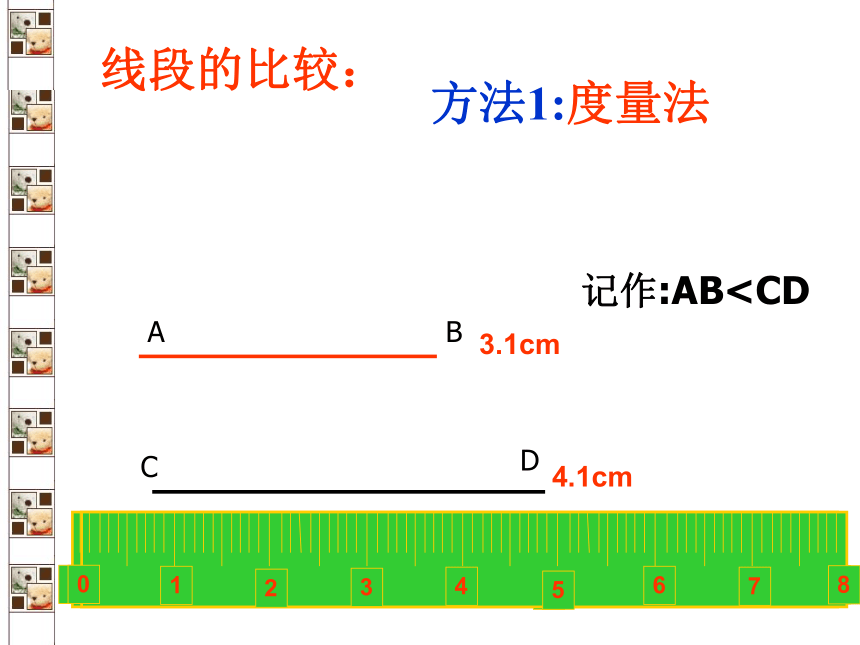
方法1:度量法
1
2
3
5
4
6
7
8
0
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
线段的比较:
A
B
C
D
记作:AB方法2:叠合法
C
D
①
A
B
②
A
B
②
A
B
C
D
E
F
E
F
M
N
M
N
AB>CD
AB=EF
AB<MN
画在黑板上的两条线段是无法移动的,在没有度
量工具的情况下,请大家想想办法,如何来比较它们
的长短?
①
观察法
② 借助某一物体,如铅笔、小木棒等。
可用圆规?
先画一条线段,再画一条与它相等的线段,
怎么画?你能想出几种方法?
可用圆规吗?
例 已知线段a用直尺和 圆规画出一条线段,使它等于已知线段a.
若另有一条线段b,你能做出线段a+b吗?2a-b呢?
你能做一条线段使它等于2a吗?
复习回顾
1、线段的性质:____________。
2、____________叫做两点之间的距离。
3、一般比较两条线段长短的方法有:
(1)、_______;
(2)、_______ 。
4、已知线段a和线段b,用用直尺和 圆规画出一条线段,使它等于2a+b。
两点之间,线段最短
连接两点之间的线段的长度
度量法
比较法
线 段 的 中 点
中点的概念 :
把一条线段分成两条相等的线段的点, 叫做这条线段的中点。 (如图点C是线段AB的中点)
A
B
C
∵C为线段AB的中点
∴AC=BC= AB;
AB = 2AC=2BC
符号语言
A
B
M
N
A
B
M
∵M、N为线段AB的三等分点
∴AM = MN = NB = AB;
AB = 3AM = 3MN = 3NB
N
P
∵ M、N、P为线段AB的四等分点
∴AN = MN = MP = PB = AB;
AB = 4AN = 4MN = 4NP= 4PB
1、如图,点C是线段AB的中点,
AC=8cm, 则BC= cm,
AB= cm.
A
B
C
8
16
2.已知线段AB的长度为2cm,延长线段AB至点C,
使BC=AB,则AC= cm
点B是线段AC的( )
4
中点
A
B
C
3.如图,AD=AB—____=AC+ _____
BD
CD
例1:如图AB=6cm,点C是线段AB的中点,点D是线段CB的中点,那么线段AD是多长呢?
A
C
B
D
1.已知线段AB=80cm,M为AB的中点,
P在MB上,N为PB的中点,且NB=14cm。
A
B
M
N
P
线段PB=________.AM=_______.BM=_______
28cm
40cm
40cm
线段PM=________.AP=_______.AN=_______
12cm
52cm
66cm
试一试
2.直线m上有A、B、C三点,且AB=8cm,BC=5cm,
求线段AC的长。
A
B
C
解:(1)当C点在线段AB的延长线上时
思考题
3.线段AB=8,在直线AB上有一点C,且BC=4,M是线段AC的中点,求线段AM的长。
M
∵AB=8,BC=4
∴AC=AB+BC=8+4=12
∵M是线段AC的中点
∴AM= AC= × 12=6
思考题
A
B
C
(2)当C点在线段AB上时
∵AB=8,BC=4
∴AC=AB-BC=8-4=4
∵M是线段AC的中点
∴AM= AC= × 4=2
M
答:线段AM的长为6或2
请同学们回顾本节课学习了哪些知识,你收获了什么?
1.线段的基本性质:两点之间线段最短。
2.两点之间的距离:两点之间线段的长度。
3.线段的两种比较方法:叠合法和度量法。
4.线段的中点的概念及表示方法。
是_____没有端点,_____只有
一个端点,_____有两个端点。
直线
线段
射线
直线的基本性质是:
____________________。
经过两点有且只有一条直线
线段、射线、直线中____可以
度量长度,所以只有____才可
以比较长短。
线段
线段
A
B
为什么有些人在A点要到马路对面B点时,不走人行横道呢?
情境1:
为什么有些人在A点要到马路对面B点时,不走人行横道呢?
情境1:
如图:从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,在图上画出最短路线.
?
?
A
B
怎样走最近?
生活常识告诉我们:两点之间的所有连线中,线段最短.简单说成:两点之间,线段最短.
线段的性质
实践出真知
连接两点间的线段的长度,叫做这两点的距离
A、B两个村庄在运河的两侧,要在运河边上建一座码头,使它到两个村庄的距离之和最小,请你确定码头的位置。
·
有四个居民小区,位置如图所示,若要建一个超市,使得超市到四个居民小区的距离之和最小,这个超市应建在何处?
A
B
C
D
问题征答
判断:
1.过A、B两点的直线长是A、B两点间的距离( )
2.两点间的连线的长度,叫做两点间的距离( )
3.两点之间的距离是指两点之间的线段 ( )
4. 连结A、B两点的所有线中,其中最短的线的长度
就是A、B两点间的距离( )
5.两点间的距离是连结两点的线段的长度。( )
错
错
错
对
对
如何比较两个人的身高?
从中你得到什么启发来比较
两条线段的长短?
情境2
方法1:度量法
1
2
3
5
4
6
7
8
0
3.1cm
4.1cm
1
2
3
5
4
6
7
8
0
线段的比较:
A
B
C
D
记作:AB
C
D
①
A
B
②
A
B
②
A
B
C
D
E
F
E
F
M
N
M
N
AB>CD
AB=EF
AB<MN
画在黑板上的两条线段是无法移动的,在没有度
量工具的情况下,请大家想想办法,如何来比较它们
的长短?
①
观察法
② 借助某一物体,如铅笔、小木棒等。
可用圆规?
先画一条线段,再画一条与它相等的线段,
怎么画?你能想出几种方法?
可用圆规吗?
例 已知线段a用直尺和 圆规画出一条线段,使它等于已知线段a.
若另有一条线段b,你能做出线段a+b吗?2a-b呢?
你能做一条线段使它等于2a吗?
复习回顾
1、线段的性质:____________。
2、____________叫做两点之间的距离。
3、一般比较两条线段长短的方法有:
(1)、_______;
(2)、_______ 。
4、已知线段a和线段b,用用直尺和 圆规画出一条线段,使它等于2a+b。
两点之间,线段最短
连接两点之间的线段的长度
度量法
比较法
线 段 的 中 点
中点的概念 :
把一条线段分成两条相等的线段的点, 叫做这条线段的中点。 (如图点C是线段AB的中点)
A
B
C
∵C为线段AB的中点
∴AC=BC= AB;
AB = 2AC=2BC
符号语言
A
B
M
N
A
B
M
∵M、N为线段AB的三等分点
∴AM = MN = NB = AB;
AB = 3AM = 3MN = 3NB
N
P
∵ M、N、P为线段AB的四等分点
∴AN = MN = MP = PB = AB;
AB = 4AN = 4MN = 4NP= 4PB
1、如图,点C是线段AB的中点,
AC=8cm, 则BC= cm,
AB= cm.
A
B
C
8
16
2.已知线段AB的长度为2cm,延长线段AB至点C,
使BC=AB,则AC= cm
点B是线段AC的( )
4
中点
A
B
C
3.如图,AD=AB—____=AC+ _____
BD
CD
例1:如图AB=6cm,点C是线段AB的中点,点D是线段CB的中点,那么线段AD是多长呢?
A
C
B
D
1.已知线段AB=80cm,M为AB的中点,
P在MB上,N为PB的中点,且NB=14cm。
A
B
M
N
P
线段PB=________.AM=_______.BM=_______
28cm
40cm
40cm
线段PM=________.AP=_______.AN=_______
12cm
52cm
66cm
试一试
2.直线m上有A、B、C三点,且AB=8cm,BC=5cm,
求线段AC的长。
A
B
C
解:(1)当C点在线段AB的延长线上时
思考题
3.线段AB=8,在直线AB上有一点C,且BC=4,M是线段AC的中点,求线段AM的长。
M
∵AB=8,BC=4
∴AC=AB+BC=8+4=12
∵M是线段AC的中点
∴AM= AC= × 12=6
思考题
A
B
C
(2)当C点在线段AB上时
∵AB=8,BC=4
∴AC=AB-BC=8-4=4
∵M是线段AC的中点
∴AM= AC= × 4=2
M
答:线段AM的长为6或2
请同学们回顾本节课学习了哪些知识,你收获了什么?
1.线段的基本性质:两点之间线段最短。
2.两点之间的距离:两点之间线段的长度。
3.线段的两种比较方法:叠合法和度量法。
4.线段的中点的概念及表示方法。
