人教版七年级数学上册课件:3.3.2解一元一次方程——去括号(共32张ppt)
文档属性
| 名称 | 人教版七年级数学上册课件:3.3.2解一元一次方程——去括号(共32张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 985.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 11:18:00 | ||
图片预览



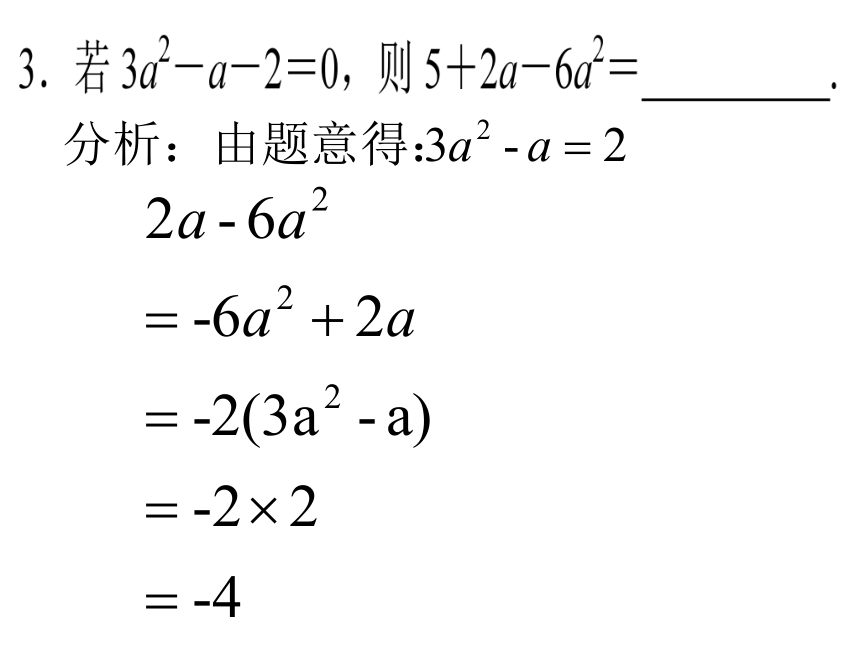

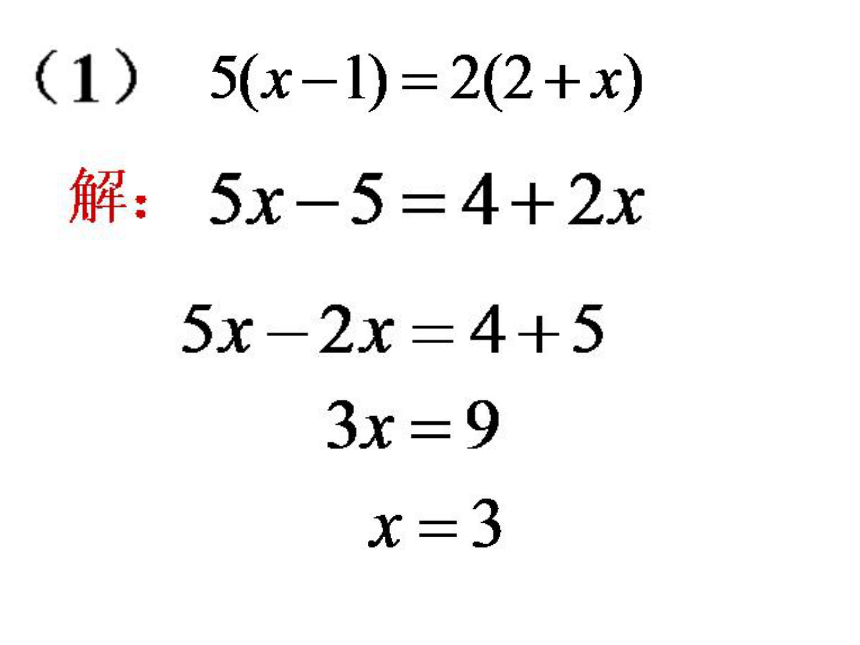





文档简介
初中七年级上册课件
§3.2.2解一元一次方程
--去括号
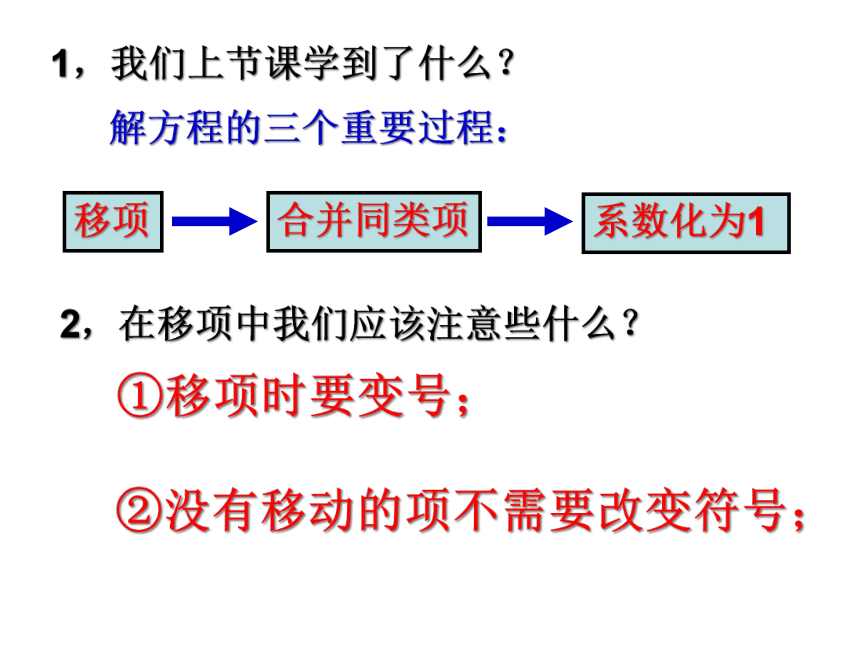
1,我们上节课学到了什么?
解方程的三个重要过程:
移项
合并同类项
系数化为1
2,在移项中我们应该注意些什么?
①移项时要变号;
②没有移动的项不需要改变符号;
练习:去括号
③ 4 ( -a +b –c )
④ -7( -x –y +z )
解:原式 =
解:原式 =
= - 4a+4b- 4c
= 7x+7y-7z
-
+
4a
4b
﹣
4c
+
+
7x
7y
﹣
7z
根据去括号知识: a-(b+c)= a-b-c
a-b-c与a-(b+c)相等;即: a-b-c也可以表示成:a-(b+c)。
整体代入思想的应用
利用整体代入法,对所求多项式进行适当变形后,再将已知条件,整体代入求值.
1.若 a+b=4,则 10-a-b=_______.
分析:已知条件为a,b;给出问题中是-a,-b;
因此添加的括号前的符号是“-”号。
救 死 扶 伤
解:原式= 8a+2b-5a-b
=(8-5)a+(2-1)b
=3a+b.
阿飞的做法有问题吗?
在化简多项式8a+2b-(5a-b) 时,阿飞的做法如下:
方程中有带括号的式子时,去括号是常用的化简步骤;
归纳:我们现在学过的解方程的一般步骤有:
移项
合并同类项
系数化为 1
去括号
去括号、移项、合并同类项、系数为化1,要注意的几个问题:
③ 合并同类项时,只是把同类项的
系数相加作为所得项的系数,字母
部分不变。
④系数化为1,要方程两边同时除以
未知数前面的系数。
②移项要变号。
①去括号要注意括号外的正、负符号。
去括号,得
移项,得
合并同类项,得
两边同除以-0.2得
下列变形对吗?若不对,请说明理由,并改正:
解 方 程
移项:
合并同类项:
解:
去括号:
系数化为 1:
这些文字说明,是为了帮助理解解方程的步骤,自己做题的时候,不用再写出来。
基 础 练 习:
方程2(x-2)-3(4x-1)=9(1-x)去括号得( )
A、2x-2-12x-3=9-9x
B、2x-4-12x-3=9-9x
C、2x-4-12x+3=9-9x
D、2x+4-12x-3=9-9x
C
1.当x取何值时代数式3x+2的值比
代数式2x-5的值大3?
3.已知x=1是关于x的方程3m+8x=1+x的解,求关于x的方程:
m+2x=2m-3x的解。
2.已知x=1是关于x的方程3m+8x=1+x
的解,求m的值。
移项:
合并同类项:
解:
去括号:
系数化为1:
移项:
合并同类项:
解:
去括号:
系数化为1:
3、下列方程解中开始出现错误的是( )
解方程:
D
A、
B、
C、
D、
(1)2(x-1)-(x+2)=3(4-x)
(2)5(x-4)-7(7-x)-9=12-3(9-x)
移项:
合并同类项:
解:
去括号:
系数化为1:
解:x=7
解下列方程:
期中数学考试后,小明、小方和小华三名同学对答案,其中有一道题三人答案各不相同,每个人都认为自己做得对.
你能帮他们检查:看看到底谁做得对吗?做错的同学又是错在哪儿呢?
一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18, 你能想出x是几吗?
小方:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
①去括号时,第二项对应
的绝对值出错。
②第三步移项时,符号出错.
一个两位数个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能想出x是几吗?
移项错
小华:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
一个两位数个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能想出x是几吗?
列方程错
小明:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
第 二 课 时
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
分析:若设上半年每月平均用电 x 度,
则下半年每月平均用电 度
上半年共用电 度,
下半年共用电 度
因为全年共用了15万度电,
所以,可列方程 。
(x-2000)
6(x-2000)
6x
6x+ 6(x-2000)=150000
基本公式:路程=速度×时间
路程:千米、米
时间:小时、、分钟、秒
速度:千米/小时、米/秒
速度 × 时间 = 路程
路程 ÷ 速度 = 时间
路程 ÷ 时间 = 速度
我们知道了速度、时间和路程
三个量中的任何两个量,都可以求
出第三个量。
一艘船从甲码头到乙码头顺流而行,用了2h;从乙码头返回甲码头逆流而行,用了2.5h;已知水流的速度是3km/h,求船在静水中的速度。
顺流的距离=逆流的距离
一艘船从甲码头到乙码头顺流而行,用了2h;从乙码头返回甲码头逆流而行,用了2.5h;已知水流的速度是3km/h,求船在静水中的速度。
分析:设船在净水中的速度为x千米/小时
顺 流
逆 流
路 程
速 度
时 间
2
2.5
(X + 3)
(X – 3)
2(X + 3)
2.5(X – 3)
在风速为24千米/小时的条件下,一架飞机顺风从A机场飞到B机场要用2.8小时,它逆风飞行同样的航线要用3小时.求:﹤1﹥飞机无风时的航速是多少千米/小时?
﹤2﹥两个机场之间的航程是多少千米?
顺 风
逆 风
路 程
速 度
时 间
2.8
3
(X + 24)
(X – 24)
2.8(X + 24)
3(X – 24)
一艘轮船从甲地顺流而行9小时到达乙地,原路返回需要11小时才能到达甲地,已知水流速度为2千米/时,求轮船在静水中的速度。
分析:设船在净水中的速度为x千米/小时
顺 流
逆 流
路 程
速 度
时 间
9
11
(X + 2)
(X – 2)
9(X + 2)
11(X – 2)
一艘船在两个码头之间航行,水流速度是3千米每小时,顺水航行需要2小时,逆水航行需要3小时,求两码头的之间的距离是多少千米?
顺 流 逆 流
一船从甲地开往乙地,顺手航行用4小时,逆水航行比顺水航行多用30分钟,已知船在静水中的速度为16km/h,求水流的速度。
顺 流 逆 流
一架飞机在两城之间飞行,顺风飞行需2小时50分,逆风飞行需3小时,飞机在无风时的速度为840千米/时,求风速是多少千米/时。
顺 流 逆 流
§3.2.2解一元一次方程
--去括号
1,我们上节课学到了什么?
解方程的三个重要过程:
移项
合并同类项
系数化为1
2,在移项中我们应该注意些什么?
①移项时要变号;
②没有移动的项不需要改变符号;
练习:去括号
③ 4 ( -a +b –c )
④ -7( -x –y +z )
解:原式 =
解:原式 =
= - 4a+4b- 4c
= 7x+7y-7z
-
+
4a
4b
﹣
4c
+
+
7x
7y
﹣
7z
根据去括号知识: a-(b+c)= a-b-c
a-b-c与a-(b+c)相等;即: a-b-c也可以表示成:a-(b+c)。
整体代入思想的应用
利用整体代入法,对所求多项式进行适当变形后,再将已知条件,整体代入求值.
1.若 a+b=4,则 10-a-b=_______.
分析:已知条件为a,b;给出问题中是-a,-b;
因此添加的括号前的符号是“-”号。
救 死 扶 伤
解:原式= 8a+2b-5a-b
=(8-5)a+(2-1)b
=3a+b.
阿飞的做法有问题吗?
在化简多项式8a+2b-(5a-b) 时,阿飞的做法如下:
方程中有带括号的式子时,去括号是常用的化简步骤;
归纳:我们现在学过的解方程的一般步骤有:
移项
合并同类项
系数化为 1
去括号
去括号、移项、合并同类项、系数为化1,要注意的几个问题:
③ 合并同类项时,只是把同类项的
系数相加作为所得项的系数,字母
部分不变。
④系数化为1,要方程两边同时除以
未知数前面的系数。
②移项要变号。
①去括号要注意括号外的正、负符号。
去括号,得
移项,得
合并同类项,得
两边同除以-0.2得
下列变形对吗?若不对,请说明理由,并改正:
解 方 程
移项:
合并同类项:
解:
去括号:
系数化为 1:
这些文字说明,是为了帮助理解解方程的步骤,自己做题的时候,不用再写出来。
基 础 练 习:
方程2(x-2)-3(4x-1)=9(1-x)去括号得( )
A、2x-2-12x-3=9-9x
B、2x-4-12x-3=9-9x
C、2x-4-12x+3=9-9x
D、2x+4-12x-3=9-9x
C
1.当x取何值时代数式3x+2的值比
代数式2x-5的值大3?
3.已知x=1是关于x的方程3m+8x=1+x的解,求关于x的方程:
m+2x=2m-3x的解。
2.已知x=1是关于x的方程3m+8x=1+x
的解,求m的值。
移项:
合并同类项:
解:
去括号:
系数化为1:
移项:
合并同类项:
解:
去括号:
系数化为1:
3、下列方程解中开始出现错误的是( )
解方程:
D
A、
B、
C、
D、
(1)2(x-1)-(x+2)=3(4-x)
(2)5(x-4)-7(7-x)-9=12-3(9-x)
移项:
合并同类项:
解:
去括号:
系数化为1:
解:x=7
解下列方程:
期中数学考试后,小明、小方和小华三名同学对答案,其中有一道题三人答案各不相同,每个人都认为自己做得对.
你能帮他们检查:看看到底谁做得对吗?做错的同学又是错在哪儿呢?
一个两位数,个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18, 你能想出x是几吗?
小方:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
①去括号时,第二项对应
的绝对值出错。
②第三步移项时,符号出错.
一个两位数个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能想出x是几吗?
移项错
小华:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
一个两位数个位上的数是2,十位上的数是x,把2和x对调,新两位数的2倍还比原两位数小18,你能想出x是几吗?
列方程错
小明:
解:
去括号,得
合并同类项,得
移项,得
系数化为1,得
第 二 课 时
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
分析:若设上半年每月平均用电 x 度,
则下半年每月平均用电 度
上半年共用电 度,
下半年共用电 度
因为全年共用了15万度电,
所以,可列方程 。
(x-2000)
6(x-2000)
6x
6x+ 6(x-2000)=150000
基本公式:路程=速度×时间
路程:千米、米
时间:小时、、分钟、秒
速度:千米/小时、米/秒
速度 × 时间 = 路程
路程 ÷ 速度 = 时间
路程 ÷ 时间 = 速度
我们知道了速度、时间和路程
三个量中的任何两个量,都可以求
出第三个量。
一艘船从甲码头到乙码头顺流而行,用了2h;从乙码头返回甲码头逆流而行,用了2.5h;已知水流的速度是3km/h,求船在静水中的速度。
顺流的距离=逆流的距离
一艘船从甲码头到乙码头顺流而行,用了2h;从乙码头返回甲码头逆流而行,用了2.5h;已知水流的速度是3km/h,求船在静水中的速度。
分析:设船在净水中的速度为x千米/小时
顺 流
逆 流
路 程
速 度
时 间
2
2.5
(X + 3)
(X – 3)
2(X + 3)
2.5(X – 3)
在风速为24千米/小时的条件下,一架飞机顺风从A机场飞到B机场要用2.8小时,它逆风飞行同样的航线要用3小时.求:﹤1﹥飞机无风时的航速是多少千米/小时?
﹤2﹥两个机场之间的航程是多少千米?
顺 风
逆 风
路 程
速 度
时 间
2.8
3
(X + 24)
(X – 24)
2.8(X + 24)
3(X – 24)
一艘轮船从甲地顺流而行9小时到达乙地,原路返回需要11小时才能到达甲地,已知水流速度为2千米/时,求轮船在静水中的速度。
分析:设船在净水中的速度为x千米/小时
顺 流
逆 流
路 程
速 度
时 间
9
11
(X + 2)
(X – 2)
9(X + 2)
11(X – 2)
一艘船在两个码头之间航行,水流速度是3千米每小时,顺水航行需要2小时,逆水航行需要3小时,求两码头的之间的距离是多少千米?
顺 流 逆 流
一船从甲地开往乙地,顺手航行用4小时,逆水航行比顺水航行多用30分钟,已知船在静水中的速度为16km/h,求水流的速度。
顺 流 逆 流
一架飞机在两城之间飞行,顺风飞行需2小时50分,逆风飞行需3小时,飞机在无风时的速度为840千米/时,求风速是多少千米/时。
顺 流 逆 流
