人教版七年级下册9.1.2不等式的性质课件(共16张ppt)
文档属性
| 名称 | 人教版七年级下册9.1.2不等式的性质课件(共16张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 251.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 11:19:57 | ||
图片预览






文档简介
不等式的性质
第九章 不等式与不等式组
教学目标
1.熟练并准确地解简单不等式, 初步体验不等式在生活中的应用;(重点)
2.根据实际意义理解不等式解的含义.(难点)
新课导入
不等式的性质1 不等式两边加(或减)同一个数(或式子), 不等号的方向不变.
不等式的性质2 不等式两边乘(或除以)同一个正数, 不等号的方向不变.
不等式的性质3 不等式两边乘(或除以)同一个负数, 不等号的方向改变.
新课导入
一辆轿车在一条规定车速不低于60km/h, 且不高于100 km/h的高速公路上行驶, 如何用式子来表示轿车在该高速公路上行驶的路程 s(km)与行驶时间 x(h)之间的关系呢?
根据路程与速度、时间之间的关系可得 s ≥ 60x, 且 s ≤ 100x.
新课导入
常用的表示不等关系的关键词语及对应的不等号:
关
键
词
语
第一类: 明确表明数量
的不等关系
第二类: 明确表明数量的范围特征
①大 于
②比…大
③超 过
①小 于
②比…小
③低 于
①不小于
②不低于
③至 少
①不大于
②不超过
③至 多
正
数
负
数
非
负
数
非
正
数
不
等
号
<
>
≥
≤
>0
<0
≥0
≤0
我们把用不等号(>, <, ≥, ≤, ≠)连接而成的式子叫作不等式. 其中 “≥” 读作大于等于, “≤” 读作小于等于.
新知探究
例 1: 某长方体形状的容器长5cm, 宽10cm, 容器内原有水的高度
为3cm, 现准备向它继续注水. 用V(单位:cm3)表示新注入水
的体积, 写出V的取值范围.
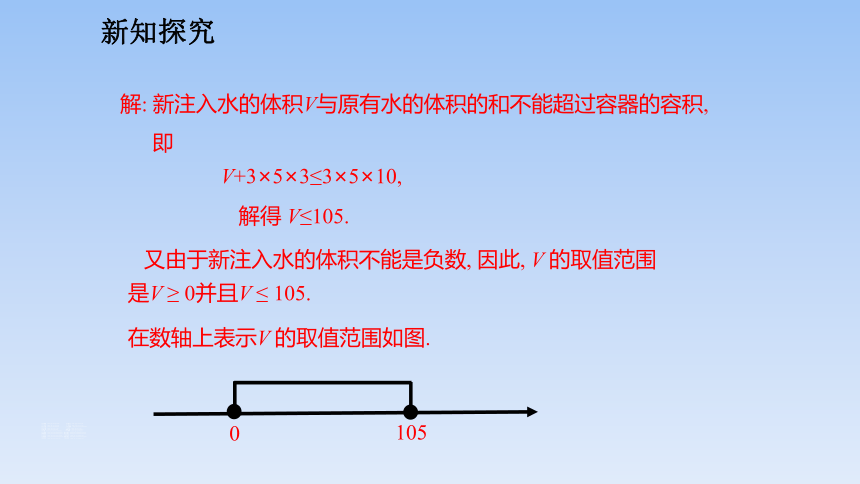
新知探究
解: 新注入水的体积V与原有水的体积的和不能超过容器的容积,
即
V+3×5×3≤3×5×10,
解得 V≤105.
又由于新注入水的体积不能是负数, 因此, V 的取值范围是V ≥ 0并且V ≤ 105.
在数轴上表示V 的取值范围如图.
0
105
知识归纳
利用不等式的性质解不等式的注意事项
2.要注意区分 “大于” “不大于” “小于” “不小于”.
等数学语言的使用, 并把这些表示不等关系的语言用数
学符号准确地表达出来.
3.在数轴上表示解集应注意的问题: 方向、空心或实心.
1.在运用性质3时, 要特别注意: 不等式两边都乘以或除以
同一个负数时, 要改变不等号的方向.
新知探究
例2: 用不等式表示下列语句并写出解集, 并在数轴上表示
解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
分析: 本题中属于第一类表示数量不等关系的关键词语.即大于或等于、不小于都用 “ ≥” 表示; 不大于、小于或等于都用 “≤” 表示.
新知探究
?
(2)x+3≥6, 解集是x≥3;
(3)y-1≤0, 解集是y≤1;
0
3
0
1
0
-8
0
?
新知探究
例3: 小希就读的学校上午第一节课上课时间是早上8点. 小希家距学校有2km, 而她的步行速度为每小时10km. 那么, 小希上午几点从家里出发才能保证不迟到?
解: 设小希上午 x 点从家里出发才能不迟到.
根据题意得
答: 小希上午7:48前时从家里出发才能不迟到.
≤8,
解得 x≤ .
课堂小结
不等式性质的应用
解不等式的依据是不等式的性质.
实际问题中的不等式的解集要符合实际意义.
课堂小测
1.若-m>5, 则m -5.
2.如果 > 0, 那么 xy 0.
3.如果 a > -1, 那么 a-b -1-b.
4.-0.9<-0.3, 两边都除以(- 0.3), 得 _______.
>
>
<
3 >1
课堂小测
5.在数轴上表示不等式 x-1<0 的解集, 正确的是 ( )
A. B.
C. D.
B
6.一种三轮车外胎上面标有 “限载280 kg” 的字样, 由此可知该
三轮车装载货物质量 x 的取值范围是 ( )
A.x < 280 kg B.x = 280 kg
C.x ≤ 280 kg D.x ≥ 280 kg
C
课堂小测
(1)5x < 200 ;
(3)x - 4 ≥ 2(x+2) ;
7.把下列不等式的解集表示在数轴上.
(4)
解:(1)
(2)
(3)
(4)
38
39
37
40
41
42
36
35
34
-11
-10
-12
-9
-8
-7
-13
-14
-15
-4
-3
-5
-2
-1
0
-6
-7
-8
(2)
1
2
3
0
-1
课堂小测
8.用炸药爆破时, 如果导火索燃烧的速度是0.8cm/s, 人跑开的速度是每秒4m,为了
使点导火索的战士在爆破时能够跑到100m以外的安全区域, 这个导火索的长度
应大于多少厘米?
答: 导火索的长度应大于20 cm.
解得 x ≥ 20.
?
解: 设导火索的长度是 x cm.
根据题意, 得
第九章 不等式与不等式组
教学目标
1.熟练并准确地解简单不等式, 初步体验不等式在生活中的应用;(重点)
2.根据实际意义理解不等式解的含义.(难点)
新课导入
不等式的性质1 不等式两边加(或减)同一个数(或式子), 不等号的方向不变.
不等式的性质2 不等式两边乘(或除以)同一个正数, 不等号的方向不变.
不等式的性质3 不等式两边乘(或除以)同一个负数, 不等号的方向改变.
新课导入
一辆轿车在一条规定车速不低于60km/h, 且不高于100 km/h的高速公路上行驶, 如何用式子来表示轿车在该高速公路上行驶的路程 s(km)与行驶时间 x(h)之间的关系呢?
根据路程与速度、时间之间的关系可得 s ≥ 60x, 且 s ≤ 100x.
新课导入
常用的表示不等关系的关键词语及对应的不等号:
关
键
词
语
第一类: 明确表明数量
的不等关系
第二类: 明确表明数量的范围特征
①大 于
②比…大
③超 过
①小 于
②比…小
③低 于
①不小于
②不低于
③至 少
①不大于
②不超过
③至 多
正
数
负
数
非
负
数
非
正
数
不
等
号
<
>
≥
≤
>0
<0
≥0
≤0
我们把用不等号(>, <, ≥, ≤, ≠)连接而成的式子叫作不等式. 其中 “≥” 读作大于等于, “≤” 读作小于等于.
新知探究
例 1: 某长方体形状的容器长5cm, 宽10cm, 容器内原有水的高度
为3cm, 现准备向它继续注水. 用V(单位:cm3)表示新注入水
的体积, 写出V的取值范围.
新知探究
解: 新注入水的体积V与原有水的体积的和不能超过容器的容积,
即
V+3×5×3≤3×5×10,
解得 V≤105.
又由于新注入水的体积不能是负数, 因此, V 的取值范围是V ≥ 0并且V ≤ 105.
在数轴上表示V 的取值范围如图.
0
105
知识归纳
利用不等式的性质解不等式的注意事项
2.要注意区分 “大于” “不大于” “小于” “不小于”.
等数学语言的使用, 并把这些表示不等关系的语言用数
学符号准确地表达出来.
3.在数轴上表示解集应注意的问题: 方向、空心或实心.
1.在运用性质3时, 要特别注意: 不等式两边都乘以或除以
同一个负数时, 要改变不等号的方向.
新知探究
例2: 用不等式表示下列语句并写出解集, 并在数轴上表示
解集.
(1)x的3倍大于或等于1;
(2)x与3的和不小于6;
(3)y与1的差不大于0;
(4)y的 小于或等于-2.
分析: 本题中属于第一类表示数量不等关系的关键词语.即大于或等于、不小于都用 “ ≥” 表示; 不大于、小于或等于都用 “≤” 表示.
新知探究
?
(2)x+3≥6, 解集是x≥3;
(3)y-1≤0, 解集是y≤1;
0
3
0
1
0
-8
0
?
新知探究
例3: 小希就读的学校上午第一节课上课时间是早上8点. 小希家距学校有2km, 而她的步行速度为每小时10km. 那么, 小希上午几点从家里出发才能保证不迟到?
解: 设小希上午 x 点从家里出发才能不迟到.
根据题意得
答: 小希上午7:48前时从家里出发才能不迟到.
≤8,
解得 x≤ .
课堂小结
不等式性质的应用
解不等式的依据是不等式的性质.
实际问题中的不等式的解集要符合实际意义.
课堂小测
1.若-m>5, 则m -5.
2.如果 > 0, 那么 xy 0.
3.如果 a > -1, 那么 a-b -1-b.
4.-0.9<-0.3, 两边都除以(- 0.3), 得 _______.
>
>
<
3 >1
课堂小测
5.在数轴上表示不等式 x-1<0 的解集, 正确的是 ( )
A. B.
C. D.
B
6.一种三轮车外胎上面标有 “限载280 kg” 的字样, 由此可知该
三轮车装载货物质量 x 的取值范围是 ( )
A.x < 280 kg B.x = 280 kg
C.x ≤ 280 kg D.x ≥ 280 kg
C
课堂小测
(1)5x < 200 ;
(3)x - 4 ≥ 2(x+2) ;
7.把下列不等式的解集表示在数轴上.
(4)
解:(1)
(2)
(3)
(4)
38
39
37
40
41
42
36
35
34
-11
-10
-12
-9
-8
-7
-13
-14
-15
-4
-3
-5
-2
-1
0
-6
-7
-8
(2)
1
2
3
0
-1
课堂小测
8.用炸药爆破时, 如果导火索燃烧的速度是0.8cm/s, 人跑开的速度是每秒4m,为了
使点导火索的战士在爆破时能够跑到100m以外的安全区域, 这个导火索的长度
应大于多少厘米?
答: 导火索的长度应大于20 cm.
解得 x ≥ 20.
?
解: 设导火索的长度是 x cm.
根据题意, 得
