人教版七年级上册数学课件:3.3解一元一次方程(一)——去括号与去分母)共15张ppt
文档属性
| 名称 | 人教版七年级上册数学课件:3.3解一元一次方程(一)——去括号与去分母)共15张ppt |

|
|
| 格式 | ppt | ||
| 文件大小 | 637.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 12:32:34 | ||
图片预览






文档简介
3.3解一元一次方程(二)
——去括号与去分母
第一课时去括号
复习
1.去括号法则.
3.解下列方程:
(1)
(2)
2.解一元一次方程的步骤.
1.去括号法则:
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
2.移项,合并同类项,系数化为1.
3.解(1)移项,得
合并同类项,得
系数化为,得
(2)移项,得
合并同类项,得
系数化为,得
一、情境引入
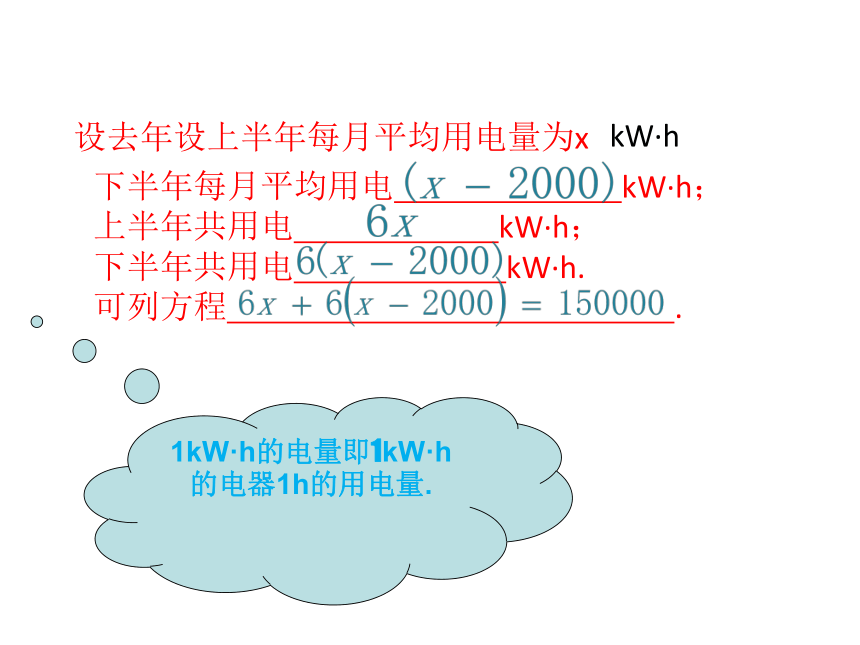
问题1:某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15 万 kW·h.这个工厂去年上半年每月平均用电是多少?
分析:题目中有哪些量、这些量存在着怎样的相等关系?
题目中的数量有:上、下半年的用电量、月平均用电量,全年用电量.
上半年的用电量+下半年的用电量=全年的用电量
下半年每月平均用电 kW·h;
上半年共用电 kW·h;
下半年共用电 kW·h.
可列方程 .
1kW·h的电量即1kW·h的电器1h的用电量.
kW·h
怎样使方程向x=a的形式转化?
范例学习
例1:解下列方程
(1)2x-(x+10)=5x+2(x-1)
(2)3x-7(x-1)=3-2(x+3)
解:(1)去括号,得
2x-x-10=5x+2x-2
移项,得
2x-x-5x-2x=10-2
合并同类项,得
-6x=8
系数化为1,得
(2)去括号,得
3x-7x+7=3-2x-3
移项,得
3x-7x+2x=3-6-7
合并同类项,得
-2x=10
系数化为1,得
x=5.
例2:一艘船从甲码头到乙码头顺流行驶,用了2h; 从乙码头返回甲码头逆流行驶,用了2.5h.已知水流的速度是3km/h,求船在静水中的平均速度.
范例学习
分析:本题数量有顺流行驶时间、逆流行驶时间、水流速度、静水速度,数量之间关系有:
顺流速度= 速度+ 速度;
逆流速度= 速度- 速度;
路程= ,
顺流路程 逆流路程.
解:设船在静水中速度是x千米/h,则顺流速度是(x+3)千米/h,逆流速度是(x-3)千米/h.
2(x+3)=2.5(x-3)
去括号,得
2x+6=2.5x-7.5
移项,得
2x-2.5x=-7.5-6
合并同类项,得
-0.5x=-13.5
系数数化为1,得
x=27
答:船在静水中一平均速度为27km/h.
列方程得,
巩固拓展
解下列方程:
(1) ;
(2) ;
(3) ;
(4) .
解:(1)去括号,得
,
合并同类项,得
,
系数化为1,得
.
(2)去括号,得
,
移项,得
,
合并同类项,得
,
系数化为1,得
.
(3)去括号,得
.
移项,得
,
合并同类项,得
,
系数数化为1,得
.
(4)去括号,得
;
移项,得
,
合并同类项,得
,
系数化为1,得
.
课堂小结
1.本节课主要学习了去括号解方程步骤及方法,去括号时注意不要漏乘,注意符号变化.
2.本节课列方程解决实际问题包含了用电问题、行程问题,问题的相等关系主要有:总量=各分量之和,顺、逆流的往返路程相等.
作业
教科书第91页习题3.3第1、6、7题
——去括号与去分母
第一课时去括号
复习
1.去括号法则.
3.解下列方程:
(1)
(2)
2.解一元一次方程的步骤.
1.去括号法则:
如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
2.移项,合并同类项,系数化为1.
3.解(1)移项,得
合并同类项,得
系数化为,得
(2)移项,得
合并同类项,得
系数化为,得
一、情境引入
问题1:某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000 kW·h(千瓦·时),全年用电15 万 kW·h.这个工厂去年上半年每月平均用电是多少?
分析:题目中有哪些量、这些量存在着怎样的相等关系?
题目中的数量有:上、下半年的用电量、月平均用电量,全年用电量.
上半年的用电量+下半年的用电量=全年的用电量
下半年每月平均用电 kW·h;
上半年共用电 kW·h;
下半年共用电 kW·h.
可列方程 .
1kW·h的电量即1kW·h的电器1h的用电量.
kW·h
怎样使方程向x=a的形式转化?
范例学习
例1:解下列方程
(1)2x-(x+10)=5x+2(x-1)
(2)3x-7(x-1)=3-2(x+3)
解:(1)去括号,得
2x-x-10=5x+2x-2
移项,得
2x-x-5x-2x=10-2
合并同类项,得
-6x=8
系数化为1,得
(2)去括号,得
3x-7x+7=3-2x-3
移项,得
3x-7x+2x=3-6-7
合并同类项,得
-2x=10
系数化为1,得
x=5.
例2:一艘船从甲码头到乙码头顺流行驶,用了2h; 从乙码头返回甲码头逆流行驶,用了2.5h.已知水流的速度是3km/h,求船在静水中的平均速度.
范例学习
分析:本题数量有顺流行驶时间、逆流行驶时间、水流速度、静水速度,数量之间关系有:
顺流速度= 速度+ 速度;
逆流速度= 速度- 速度;
路程= ,
顺流路程 逆流路程.
解:设船在静水中速度是x千米/h,则顺流速度是(x+3)千米/h,逆流速度是(x-3)千米/h.
2(x+3)=2.5(x-3)
去括号,得
2x+6=2.5x-7.5
移项,得
2x-2.5x=-7.5-6
合并同类项,得
-0.5x=-13.5
系数数化为1,得
x=27
答:船在静水中一平均速度为27km/h.
列方程得,
巩固拓展
解下列方程:
(1) ;
(2) ;
(3) ;
(4) .
解:(1)去括号,得
,
合并同类项,得
,
系数化为1,得
.
(2)去括号,得
,
移项,得
,
合并同类项,得
,
系数化为1,得
.
(3)去括号,得
.
移项,得
,
合并同类项,得
,
系数数化为1,得
.
(4)去括号,得
;
移项,得
,
合并同类项,得
,
系数化为1,得
.
课堂小结
1.本节课主要学习了去括号解方程步骤及方法,去括号时注意不要漏乘,注意符号变化.
2.本节课列方程解决实际问题包含了用电问题、行程问题,问题的相等关系主要有:总量=各分量之和,顺、逆流的往返路程相等.
作业
教科书第91页习题3.3第1、6、7题
