人教版数学八年级上册13.1.2线段垂直平分线的性质 课件(共18张ppt)
文档属性
| 名称 | 人教版数学八年级上册13.1.2线段垂直平分线的性质 课件(共18张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 11:24:32 | ||
图片预览




文档简介
第十三章 轴对称
13.1.2线段的垂直平分线的性质
英山县政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
生活中的数学
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线
∵ AC=BC, CD ⊥AB,
∴ CD是AB的垂直平分线
A
B
C
D
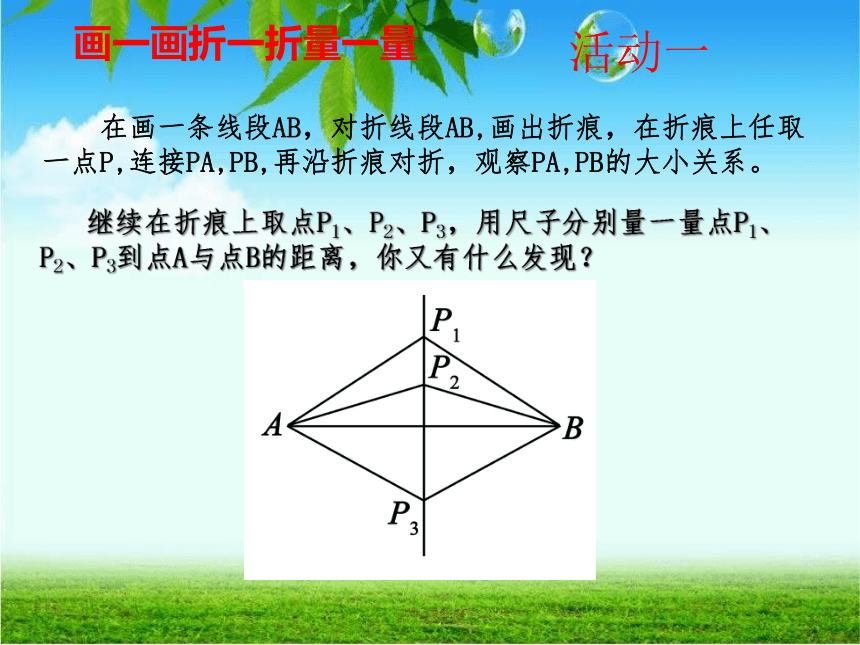
继续在折痕上取点P1、P2、P3,用尺子分别量一量点P1、P2、P3到点A与点B的距离,你又有什么发现?
画一画折一折量一量
活动一
在画一条线段AB,对折线段AB,画出折痕,在折痕上任取一点P,连接PA,PB,再沿折痕对折,观察PA,PB的大小关系。
自学提纲:
在纸上画一条线段AB,对折线段,思考如下问题:
(1)线段——(填“是”或“不是”)轴对称图形;
(2)折痕与线段——(填“垂直”或“不垂直”;)
(3)这条折痕是线段AB的————
(4)在折痕上任找一点P,连接PA和PB,量一量PA与PB的长,PA与PB的关系是 ————(填“相等”或“不相等”)
(5)通过测量,你发现P1A P1B; P2A P2B
P3A P3B
由此你能得到什么结论?
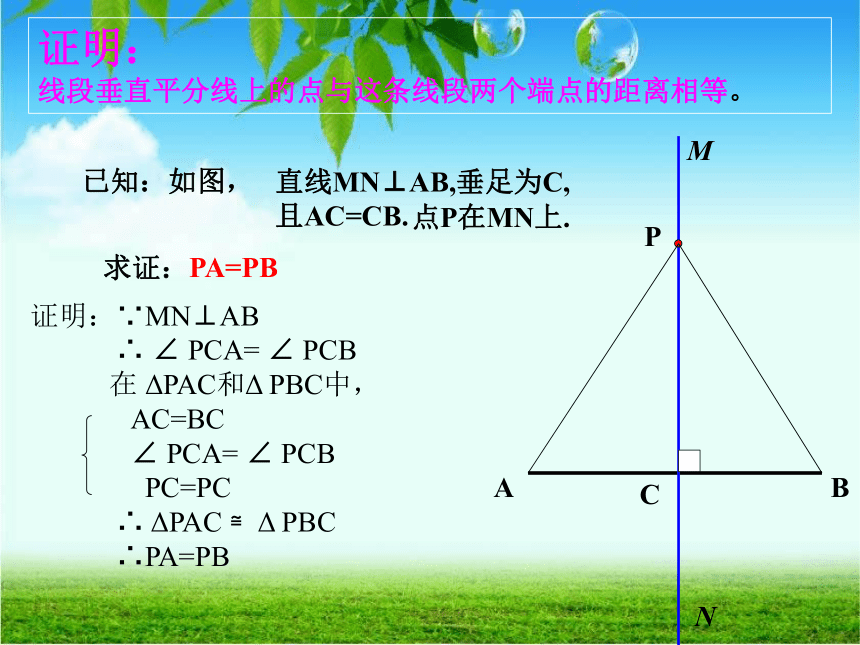
证明:
线段垂直平分线上的点与这条线段两个端点的距离相等。
A
B
P
M
N
C
PA=PB
直线MN⊥AB,垂足为C,
且AC=CB.
已知:如图,
点P在MN上.
求证:
证明:∵MN⊥AB
∴ ∠ PCA= ∠ PCB
在 ΔPAC和Δ PBC中,
AC=BC
∠ PCA= ∠ PCB
PC=PC
∴ ΔPAC ≌Δ PBC
∴PA=PB
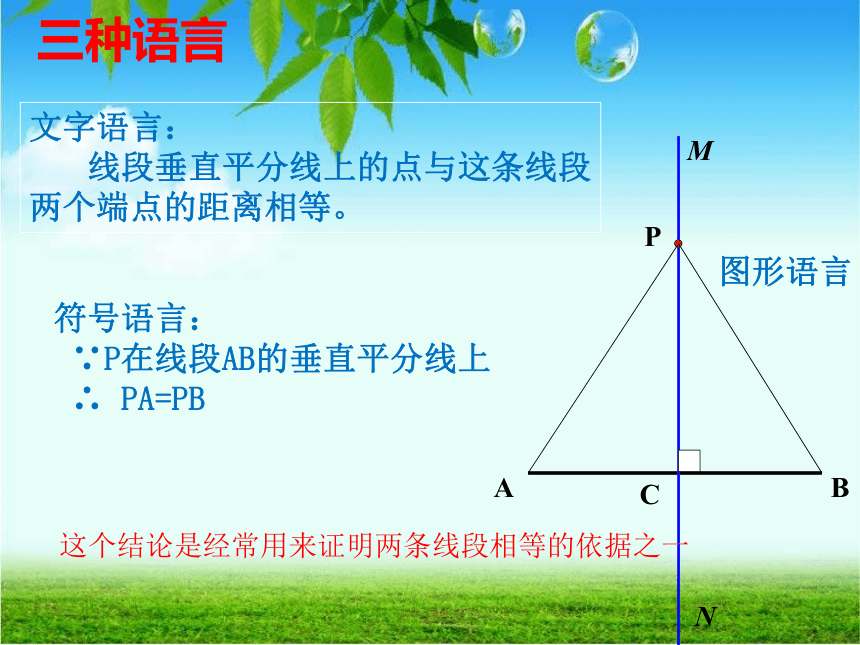
文字语言:
线段垂直平分线上的点与这条线段 两个端点的距离相等。
A
B
P
M
N
C
三种语言
图形语言
这个结论是经常用来证明两条线段相等的依据之一
符号语言:
∵P在线段AB的垂直平分线上
∴ PA=PB
游戏中的数学
C
D
实战演练
2、如图,在△ABC中,ED垂直平分AB,
1) 若BD=10,则AD=
2) 若AC=14,△BCD的周长为24,则BC= 。
实战演练
BD=CD
线段垂直平
分线上的点到线段两端点的距离相等.
实战演练
思考分析
反过来: 如果PA=PB,P在线段AB的垂直平分线上吗?你能证明吗?
A
B
P
已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.
.
C
活动二
方法归纳:
1,作垂直,证平分;2作平分,证垂直
文字语言:
到线段两个端点的距离相等的点在线段的垂直平分线上。
A
B
P
M
N
C
三种语言
图形语言
这个结论是经常用来证明点在直线上或直线过某一点的依据之一
符号语言:
∵PA=PB
∴ P在线段AB的垂直平分线上
思考:
满足PA=PB的点P有多少个?这些点合在一起组成
了什么图形?
本题主要考查:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上;两点确定一条直线.
?
A.AB垂直平分CD???? B.CD垂直平分AB
C.AB与CD互相垂直平分? D.CD平分∠ACB
如图,AC=AD,BC=BD,则有( ).
实战演练
反之:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线
性质:线段垂直平分线上的点与这条线段两个端点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点与这条线段两个端点的距离相等
·
英山县政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
思考:生活中的数学
数学问题源于生活实践,反过来数学又为生活实践服务
B
A
C
M
N
M’
N’
P
你能依据这一问题得到什么结论?
结论: 三角形三边垂直平分线交于一点,
这一点到三角形三个顶点的距离相等。
实际问题
数学化
再 见!
13.1.2线段的垂直平分线的性质
英山县政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
生活中的数学
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线
∵ AC=BC, CD ⊥AB,
∴ CD是AB的垂直平分线
A
B
C
D
继续在折痕上取点P1、P2、P3,用尺子分别量一量点P1、P2、P3到点A与点B的距离,你又有什么发现?
画一画折一折量一量
活动一
在画一条线段AB,对折线段AB,画出折痕,在折痕上任取一点P,连接PA,PB,再沿折痕对折,观察PA,PB的大小关系。
自学提纲:
在纸上画一条线段AB,对折线段,思考如下问题:
(1)线段——(填“是”或“不是”)轴对称图形;
(2)折痕与线段——(填“垂直”或“不垂直”;)
(3)这条折痕是线段AB的————
(4)在折痕上任找一点P,连接PA和PB,量一量PA与PB的长,PA与PB的关系是 ————(填“相等”或“不相等”)
(5)通过测量,你发现P1A P1B; P2A P2B
P3A P3B
由此你能得到什么结论?
证明:
线段垂直平分线上的点与这条线段两个端点的距离相等。
A
B
P
M
N
C
PA=PB
直线MN⊥AB,垂足为C,
且AC=CB.
已知:如图,
点P在MN上.
求证:
证明:∵MN⊥AB
∴ ∠ PCA= ∠ PCB
在 ΔPAC和Δ PBC中,
AC=BC
∠ PCA= ∠ PCB
PC=PC
∴ ΔPAC ≌Δ PBC
∴PA=PB
文字语言:
线段垂直平分线上的点与这条线段 两个端点的距离相等。
A
B
P
M
N
C
三种语言
图形语言
这个结论是经常用来证明两条线段相等的依据之一
符号语言:
∵P在线段AB的垂直平分线上
∴ PA=PB
游戏中的数学
C
D
实战演练
2、如图,在△ABC中,ED垂直平分AB,
1) 若BD=10,则AD=
2) 若AC=14,△BCD的周长为24,则BC= 。
实战演练
BD=CD
线段垂直平
分线上的点到线段两端点的距离相等.
实战演练
思考分析
反过来: 如果PA=PB,P在线段AB的垂直平分线上吗?你能证明吗?
A
B
P
已知:如图,PA=PB.
求证:点P在AB的垂直平分线上.
.
C
活动二
方法归纳:
1,作垂直,证平分;2作平分,证垂直
文字语言:
到线段两个端点的距离相等的点在线段的垂直平分线上。
A
B
P
M
N
C
三种语言
图形语言
这个结论是经常用来证明点在直线上或直线过某一点的依据之一
符号语言:
∵PA=PB
∴ P在线段AB的垂直平分线上
思考:
满足PA=PB的点P有多少个?这些点合在一起组成
了什么图形?
本题主要考查:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上;两点确定一条直线.
?
A.AB垂直平分CD???? B.CD垂直平分AB
C.AB与CD互相垂直平分? D.CD平分∠ACB
如图,AC=AD,BC=BD,则有( ).
实战演练
反之:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
线段的垂直平分线
性质:线段垂直平分线上的点与这条线段两个端点的距离相等。
PA=PB
点P在线段AB的垂直平分线上
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上
线段垂直平分线上的点与这条线段两个端点的距离相等
·
英山县政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
思考:生活中的数学
数学问题源于生活实践,反过来数学又为生活实践服务
B
A
C
M
N
M’
N’
P
你能依据这一问题得到什么结论?
结论: 三角形三边垂直平分线交于一点,
这一点到三角形三个顶点的距离相等。
实际问题
数学化
再 见!
