沪科版数学九年级上期末复习题(二)(word版无答案)
文档属性
| 名称 | 沪科版数学九年级上期末复习题(二)(word版无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 126.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 19:34:45 | ||
图片预览


文档简介
沪科版数学九年级上期末复习专题
第1题
抛物线y=x2-2的顶点坐标是( )
A.(0,2) B.(0,-2) C.(-2,0) D.(2,0)
第2题
在反比例函数y=图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k<0 B.k>0 C.k<1 D.k>1
第3题
如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )
A.1∶ B.∶4 C.1∶2 D.1∶4
第4题
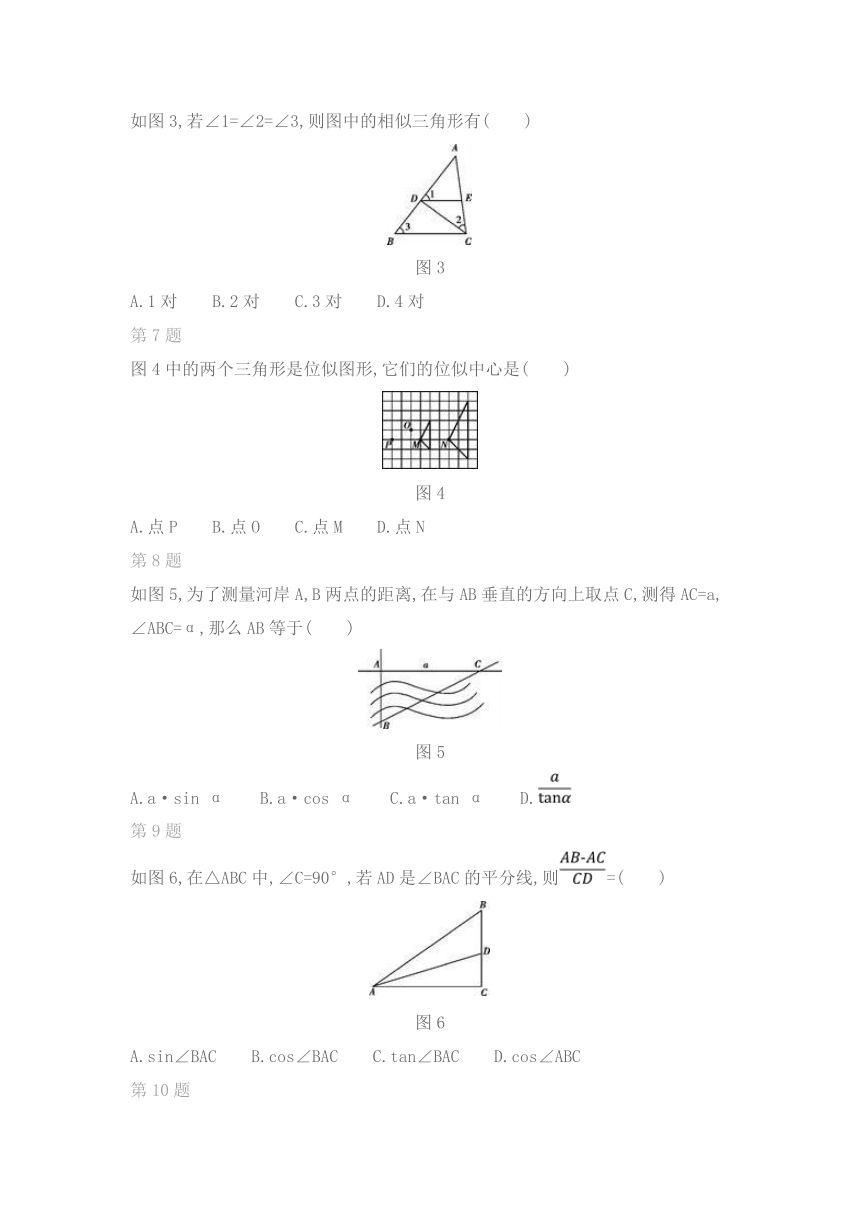
如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=,BC=2.则sin∠ACD的值为( )
图1
A. B. C. D.
第5题
如图2,已知AB∥CD∥EF,那么下列结论正确的是( )
图2
A.= B.= C.= D.=
第6题
如图3,若∠1=∠2=∠3,则图中的相似三角形有( )
图3
A.1对 B.2对 C.3对 D.4对
第7题
图4中的两个三角形是位似图形,它们的位似中心是( )
图4
A.点P B.点O C.点M D.点N
第8题
如图5,为了测量河岸A,B两点的距离,在与AB垂直的方向上取点C,测得AC=a,∠ABC=α,那么AB等于( )
图5
A.a·sin
α B.a·cos
α C.a·tan
α D.
第9题
如图6,在△ABC中,∠C=90°,若AD是∠BAC的平分线,则=( )
图6
A.sin∠BAC B.cos∠BAC C.tan∠BAC D.cos∠ABC
第10题
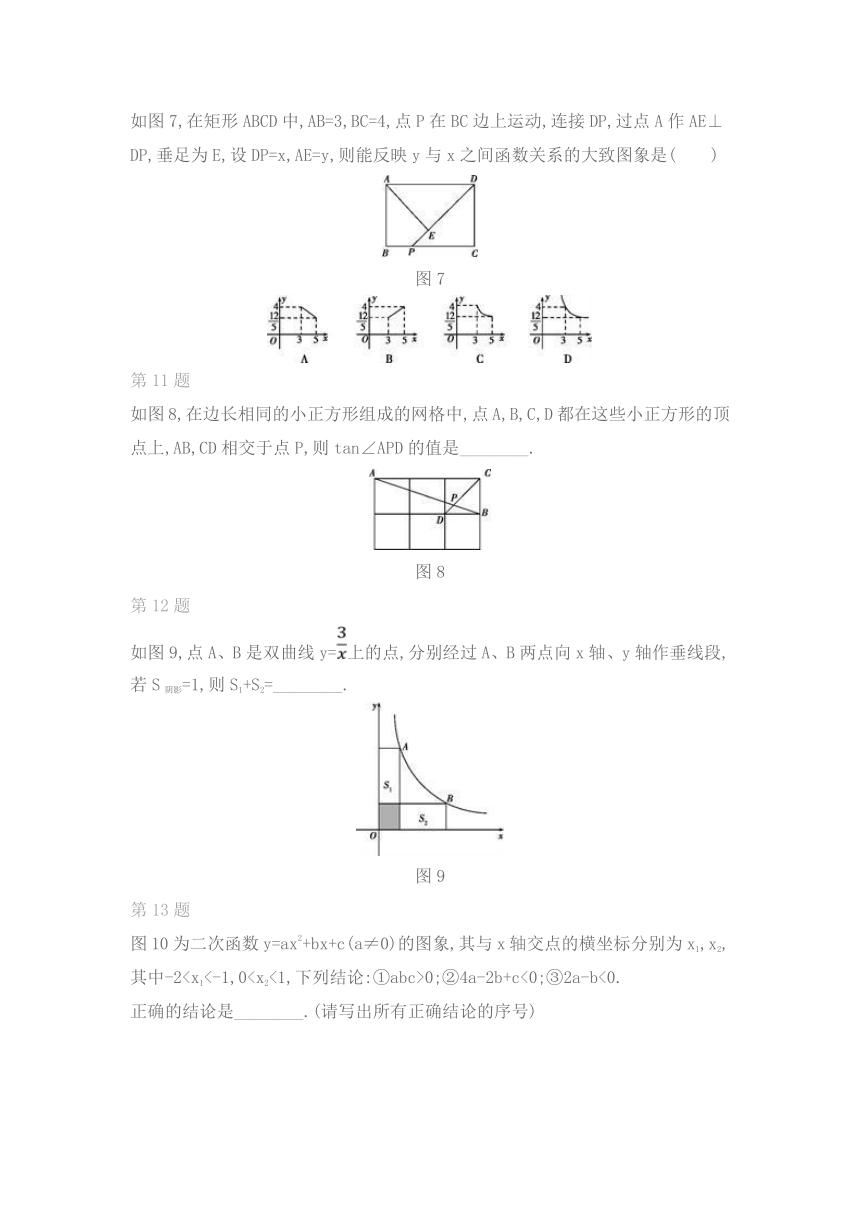
如图7,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连接DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )
图7
第11题
如图8,在边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则tan∠APD的值是________.
图8
第12题
如图9,点A、B是双曲线y=上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=________.
图9
第13题
图10为二次函数y=ax2+bx+c(a≠0)的图象,其与x轴交点的横坐标分别为x1,x2,其中-20;②4a-2b+c<0;③2a-b<0.
正确的结论是________.(请写出所有正确结论的序号)
图10
第14题
如图11(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE—ED—DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1
cm/s,设P、Q出发t
s时,△BPQ的面积为y
cm2.已知y与t的函数关系如图11(2)所示(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②cos∠ABE=;③当0(1) (2)
图11
三、(本大题共2小题,每小题8分,满分16分)
第15题
计算:sin
80°+-tan
30°+(1-sin
75°)0-cos
10°.
第16题
已知抛物线y=x2-4x+7与y=x交于A、B两点(A点在B点左侧).
(1)求A、B两点的坐标;
(2)求抛物线顶点C的坐标,并求△ABC的面积.
四、(本大题共2小题,每小题8分,满分16分)
第17题
已知x∶y∶z=3∶4∶5.
(1)求的值;
(2)若x+y+z=6,求x、y、z.
第18题
如图12,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
图12
(1)画出位似中心点O;
(2)求出△ABC与△A'B'C'的位似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
五、(本大题共2小题,每小题10分,满分20分)
第19题
如图13,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1∶,AB=8米,AE=12米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米)
参考数据:≈1.414,≈1.732.
图13
第20题
已知一次函数与反比例函数的图象交于P(-3,m),Q(2,-3).
(1)求这两个函数的函数关系式;
(2)在给定的直角坐标系(如图14)中,画出这两个函数的大致图象;
(3)点C(a,b)在反比例函数的图象上,当1≤a≤3时,求b的取值范围.
图14
六、(本题满分12分)
第21题
如图15,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕与边BC交于点O,AD=8.
(1)求证:△ADP∽△PCO;
(2)若△OCP与△PDA的面积比为1∶4,求边AB的长;
(3)若图中的点P恰好是CD边的中点,求∠OAB的度数.
图15
七、(本题满分12分)
第22题
某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为w=-2x+240.设这种绿茶在这段时间内的销售利润为y元,解答下列问题:
(1)求y与x的关系式;
(2)当x取何值时,y的值最大?
(3)如果物价部门规定这种绿茶的销售价不得高于90元/千克,公司想要在这段时间内获得2
250元的销售利润,问销售单价应定为多少元?
八、(本题满分14分)
第23题
已知等腰直角△ABC中,∠BAC=90°,AB=AC=2,动点P在直线BC上运动(不与点B、C重合).
(1)如图16a,点P在线段BC上,作∠APQ=45°,PQ交AC于点Q.
①求证:△ABP∽△PCQ;
②当△APQ是等腰三角形时,求AQ的长.
(2)①如图16b,点P在BC的延长线上,作∠APQ=45°,PQ的反向延长线与AC的延长线相交于点D,是否存在点P,使△APD是等腰三角形?若存在,写出点P的位置;若不存在,请简要说明理由;
②如图16c,点P在CB的延长线上,作∠APQ=45°,PQ与AC的延长线相交于点Q,是否存在点P,使△APQ是等腰三角形?若存在,写出点P的位置;若不存在,请简要说明理由.
图16
第1题
抛物线y=x2-2的顶点坐标是( )
A.(0,2) B.(0,-2) C.(-2,0) D.(2,0)
第2题
在反比例函数y=图象的每一支曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k<0 B.k>0 C.k<1 D.k>1
第3题
如果两个相似三角形的面积比是1∶4,那么它们的周长比是( )
A.1∶ B.∶4 C.1∶2 D.1∶4
第4题
如图1,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=,BC=2.则sin∠ACD的值为( )
图1
A. B. C. D.
第5题
如图2,已知AB∥CD∥EF,那么下列结论正确的是( )
图2
A.= B.= C.= D.=
第6题
如图3,若∠1=∠2=∠3,则图中的相似三角形有( )
图3
A.1对 B.2对 C.3对 D.4对
第7题
图4中的两个三角形是位似图形,它们的位似中心是( )
图4
A.点P B.点O C.点M D.点N
第8题
如图5,为了测量河岸A,B两点的距离,在与AB垂直的方向上取点C,测得AC=a,∠ABC=α,那么AB等于( )
图5
A.a·sin
α B.a·cos
α C.a·tan
α D.
第9题
如图6,在△ABC中,∠C=90°,若AD是∠BAC的平分线,则=( )
图6
A.sin∠BAC B.cos∠BAC C.tan∠BAC D.cos∠ABC
第10题
如图7,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连接DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是( )
图7
第11题
如图8,在边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则tan∠APD的值是________.
图8
第12题
如图9,点A、B是双曲线y=上的点,分别经过A、B两点向x轴、y轴作垂线段,若S阴影=1,则S1+S2=________.
图9
第13题
图10为二次函数y=ax2+bx+c(a≠0)的图象,其与x轴交点的横坐标分别为x1,x2,其中-2
正确的结论是________.(请写出所有正确结论的序号)
图10
第14题
如图11(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE—ED—DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1
cm/s,设P、Q出发t
s时,△BPQ的面积为y
cm2.已知y与t的函数关系如图11(2)所示(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②cos∠ABE=;③当0
图11
三、(本大题共2小题,每小题8分,满分16分)
第15题
计算:sin
80°+-tan
30°+(1-sin
75°)0-cos
10°.
第16题
已知抛物线y=x2-4x+7与y=x交于A、B两点(A点在B点左侧).
(1)求A、B两点的坐标;
(2)求抛物线顶点C的坐标,并求△ABC的面积.
四、(本大题共2小题,每小题8分,满分16分)
第17题
已知x∶y∶z=3∶4∶5.
(1)求的值;
(2)若x+y+z=6,求x、y、z.
第18题
如图12,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.
图12
(1)画出位似中心点O;
(2)求出△ABC与△A'B'C'的位似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
五、(本大题共2小题,每小题10分,满分20分)
第19题
如图13,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1∶,AB=8米,AE=12米.
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米)
参考数据:≈1.414,≈1.732.
图13
第20题
已知一次函数与反比例函数的图象交于P(-3,m),Q(2,-3).
(1)求这两个函数的函数关系式;
(2)在给定的直角坐标系(如图14)中,画出这两个函数的大致图象;
(3)点C(a,b)在反比例函数的图象上,当1≤a≤3时,求b的取值范围.
图14
六、(本题满分12分)
第21题
如图15,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕与边BC交于点O,AD=8.
(1)求证:△ADP∽△PCO;
(2)若△OCP与△PDA的面积比为1∶4,求边AB的长;
(3)若图中的点P恰好是CD边的中点,求∠OAB的度数.
图15
七、(本题满分12分)
第22题
某公司经销一种绿茶,每千克成本为50元.市场调查发现,在一段时间内,销售量w(千克)随销售单价x(元/千克)的变化而变化,具体关系式为w=-2x+240.设这种绿茶在这段时间内的销售利润为y元,解答下列问题:
(1)求y与x的关系式;
(2)当x取何值时,y的值最大?
(3)如果物价部门规定这种绿茶的销售价不得高于90元/千克,公司想要在这段时间内获得2
250元的销售利润,问销售单价应定为多少元?
八、(本题满分14分)
第23题
已知等腰直角△ABC中,∠BAC=90°,AB=AC=2,动点P在直线BC上运动(不与点B、C重合).
(1)如图16a,点P在线段BC上,作∠APQ=45°,PQ交AC于点Q.
①求证:△ABP∽△PCQ;
②当△APQ是等腰三角形时,求AQ的长.
(2)①如图16b,点P在BC的延长线上,作∠APQ=45°,PQ的反向延长线与AC的延长线相交于点D,是否存在点P,使△APD是等腰三角形?若存在,写出点P的位置;若不存在,请简要说明理由;
②如图16c,点P在CB的延长线上,作∠APQ=45°,PQ与AC的延长线相交于点Q,是否存在点P,使△APQ是等腰三角形?若存在,写出点P的位置;若不存在,请简要说明理由.
图16
同课章节目录
