人教版数学九年级下册26.1.2反比例函数的图象和性质-课件(共22张ppt)
文档属性
| 名称 | 人教版数学九年级下册26.1.2反比例函数的图象和性质-课件(共22张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 12:03:49 | ||
图片预览








文档简介
一、教学设计意图
本节课帮助学生梳理知识脉络,理清做题思路,建构知识网络,使所学知识更加条理化、系统化,在学生已掌握的基础上,查补缺漏、拓展延伸。本节课以问题为主线,练习为核心,活动为载体,从学生已有的学习经验和认知基础出发,引导其经历复习加深理解反比例函数中比例系数K的几何意义及应用。
二、考点分析
反比例函数是历年中考数学的一个重要考点章节,且多以大题的形式出现,常常结合三角形,四边形等相关知识综合考察。所以,应该引起广大学生的重视。反比例函数中k的几何意义也是其中一块很重要的知识章节,常在中考选择题,计算大题中进行考察。这类考题大多考点简单但方法灵活,目的在于考察学生的数学图形思维。本次专题目的在于让学生掌握反比例函数k几何意义这一知识要点,灵活利用这一知识点解决数学问题,并熟悉与反比例函数k几何意义的常见考察方式和解题思路。
三、学情分析
教学对象是九年级学生,本专题是对反比例函数K的几何意义的再现和综合运用,在复习本课前,学生已经基本掌握了反比例基本知识和基本技能,本专题旨在通过复习使学生更加灵活利用这一知识点解决数学问题,并熟悉与反比例函数k几何意义的常见考察方式和解题思路。
1.知识目标:
了解反比例函数中“k”的值与相应矩形及三角形面积之间的关系
2.能力目标:
逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数中比例系数“k”的几何意义,培养学生类比、转化及数形结合的数学思想方法。
3.情感目标:
通过对图象性质的研究,训练学生的探索能力,语言组织能力和分析问题及解决问题的能力.
四:目标要求:
五、教法、学法
常言道:教必有法,教无定法。这节课我采用考点聚焦、归类探究、方法点析、回归教材探索发现法,培养学生学习数学的积极性,精心引导学生通过反比例函数模型实现解决问题的方法。在引导过程中让学生体会数形结合、转化与化归、函数与方程、分类讨论的数学思想。
古人云“授人以鱼,不如授人以渔”这节课我引导学生采用自主探究,合作交流,自我总结的学习方法,体现数学探索的乐趣。
(1)、重点:
通过观察图象,概括反比例函数图象的共同特征,探索反比例函数的比例系数“k”的几何意义.
(2)、难点:
从反比例函数的图象中归纳总结反比例函数的主要性质及综合应用.
六、教学重难点
七、教学过程
德育三分钟课堂
《疯狂的蒲公英》
——献给所有有梦想的人,激 励学生备战中考。
x
y
O
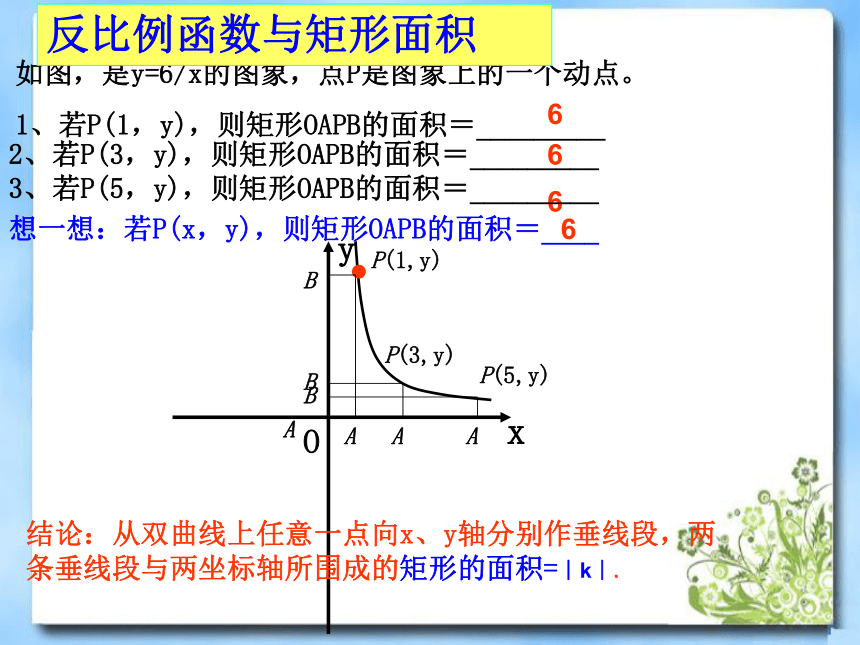
如图,是y=6/x的图象,点P是图象上的一个动点。
1、若P(1,y),则矩形OAPB的面积=_________
P(1,y)
B
B
A
A
A
B
A
P(5,y)
P(3,y)
2、若P(3,y),则矩形OAPB的面积=_________
6
6
6
3、若P(5,y),则矩形OAPB的面积=_________
结论:从双曲线上任意一点向x、y轴分别作垂线段,两条垂线段与两坐标轴所围成的矩形的面积=︱k︱.
想一想:若P(x,y),则矩形OAPB的面积=____
6
反比例函数与矩形面积
P(m,n)
A
o
y
x
过P作x轴的垂线,垂足为A,则它与坐标轴形成的三角形的面积是不变的,为:
推广:反比例函数与三角形面积
A
A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3
B
A1
o
y
x
A
C
B1
C1
S1
S3
S2
一 、千里之行 始于足下
P
D
o
y
x
2.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
1
一、 千里之行 始于足下
3.如图,点A,B是双曲线 上的点,过点A、B两点分别向x轴、y轴作垂线,若S阴影=1,则S1+S2=
x
y
A
B
O
4
4
S1
S2
S3
B
y
x
P
A
1. 已知点A是反比例函数 上的点,过点A作
AP⊥x轴于点P,已知△AOP的面积3,则k的值是( )
A. 6 B. -6
C.-3 D. 3
P
C
O
?像这样的图形变换叫等积变换
二、趁热打铁,大显身手
x
y
O
A
B
C
如图反比例函数 与正比例函数y=kx相交于点A、点B。
(1)AC⊥x轴,则△OAC的面积是____
(2)连接BC,则△OBC的面积是____,
D
(3)△ABC的面积是____
12
6
6
(4)△ABD的面积____
48
24
(5) ADBE的=____
E
(6) ACBF的面积____
F
24
S
1.(辽宁)反比例函数 与 在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )
A. B.2 C.3 D.1
A
C
二、趁热打铁,大显身手
x
y
O
2、如图反比例函数 与正比例函数 相交于点A、B. AC⊥BC,则△ABC的面积是________.
D
C
A
B
方法1:计算.设A(x,y),
则△ABC的面积=
方法2:连接OC,
利用对称
方法3:构造长方形
3.(湖北孝感) 如图,点A在双曲线
上,点B在双曲线 上,且AB∥x轴,C、
D在x轴上,若四边形ABCD为矩形,则它的
面积为 .
E
4(年陕西)如图,过y轴正半轴上的任意一点P,作x
轴的平行线,分别与反比例函数y=- 和y= 图象交于点
A和点B.若点C 是x轴上任意一点,连接AC、BC,则△ABC的面
积为 ( )
A.3 B.4
C.5 D.6
A
反比例函数中的面积问题
以形助数 用数解形
一个性质:反比例函数的面积不变性
多种思想:
数形结合
分类讨论
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考, 去发现,去总结。
本节课帮助学生梳理知识脉络,理清做题思路,建构知识网络,使所学知识更加条理化、系统化,在学生已掌握的基础上,查补缺漏、拓展延伸。本节课以问题为主线,练习为核心,活动为载体,从学生已有的学习经验和认知基础出发,引导其经历复习加深理解反比例函数中比例系数K的几何意义及应用。
二、考点分析
反比例函数是历年中考数学的一个重要考点章节,且多以大题的形式出现,常常结合三角形,四边形等相关知识综合考察。所以,应该引起广大学生的重视。反比例函数中k的几何意义也是其中一块很重要的知识章节,常在中考选择题,计算大题中进行考察。这类考题大多考点简单但方法灵活,目的在于考察学生的数学图形思维。本次专题目的在于让学生掌握反比例函数k几何意义这一知识要点,灵活利用这一知识点解决数学问题,并熟悉与反比例函数k几何意义的常见考察方式和解题思路。
三、学情分析
教学对象是九年级学生,本专题是对反比例函数K的几何意义的再现和综合运用,在复习本课前,学生已经基本掌握了反比例基本知识和基本技能,本专题旨在通过复习使学生更加灵活利用这一知识点解决数学问题,并熟悉与反比例函数k几何意义的常见考察方式和解题思路。
1.知识目标:
了解反比例函数中“k”的值与相应矩形及三角形面积之间的关系
2.能力目标:
逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数中比例系数“k”的几何意义,培养学生类比、转化及数形结合的数学思想方法。
3.情感目标:
通过对图象性质的研究,训练学生的探索能力,语言组织能力和分析问题及解决问题的能力.
四:目标要求:
五、教法、学法
常言道:教必有法,教无定法。这节课我采用考点聚焦、归类探究、方法点析、回归教材探索发现法,培养学生学习数学的积极性,精心引导学生通过反比例函数模型实现解决问题的方法。在引导过程中让学生体会数形结合、转化与化归、函数与方程、分类讨论的数学思想。
古人云“授人以鱼,不如授人以渔”这节课我引导学生采用自主探究,合作交流,自我总结的学习方法,体现数学探索的乐趣。
(1)、重点:
通过观察图象,概括反比例函数图象的共同特征,探索反比例函数的比例系数“k”的几何意义.
(2)、难点:
从反比例函数的图象中归纳总结反比例函数的主要性质及综合应用.
六、教学重难点
七、教学过程
德育三分钟课堂
《疯狂的蒲公英》
——献给所有有梦想的人,激 励学生备战中考。
x
y
O
如图,是y=6/x的图象,点P是图象上的一个动点。
1、若P(1,y),则矩形OAPB的面积=_________
P(1,y)
B
B
A
A
A
B
A
P(5,y)
P(3,y)
2、若P(3,y),则矩形OAPB的面积=_________
6
6
6
3、若P(5,y),则矩形OAPB的面积=_________
结论:从双曲线上任意一点向x、y轴分别作垂线段,两条垂线段与两坐标轴所围成的矩形的面积=︱k︱.
想一想:若P(x,y),则矩形OAPB的面积=____
6
反比例函数与矩形面积
P(m,n)
A
o
y
x
过P作x轴的垂线,垂足为A,则它与坐标轴形成的三角形的面积是不变的,为:
推广:反比例函数与三角形面积
A
A.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3
B
A1
o
y
x
A
C
B1
C1
S1
S3
S2
一 、千里之行 始于足下
P
D
o
y
x
2.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .
1
一、 千里之行 始于足下
3.如图,点A,B是双曲线 上的点,过点A、B两点分别向x轴、y轴作垂线,若S阴影=1,则S1+S2=
x
y
A
B
O
4
4
S1
S2
S3
B
y
x
P
A
1. 已知点A是反比例函数 上的点,过点A作
AP⊥x轴于点P,已知△AOP的面积3,则k的值是( )
A. 6 B. -6
C.-3 D. 3
P
C
O
?像这样的图形变换叫等积变换
二、趁热打铁,大显身手
x
y
O
A
B
C
如图反比例函数 与正比例函数y=kx相交于点A、点B。
(1)AC⊥x轴,则△OAC的面积是____
(2)连接BC,则△OBC的面积是____,
D
(3)△ABC的面积是____
12
6
6
(4)△ABD的面积____
48
24
(5) ADBE的=____
E
(6) ACBF的面积____
F
24
S
1.(辽宁)反比例函数 与 在第一象限的图象如图所示,作一条平行于x轴的直线分别交双曲线于A、B两点,连接OA、OB,则△AOB的面积为( )
A. B.2 C.3 D.1
A
C
二、趁热打铁,大显身手
x
y
O
2、如图反比例函数 与正比例函数 相交于点A、B. AC⊥BC,则△ABC的面积是________.
D
C
A
B
方法1:计算.设A(x,y),
则△ABC的面积=
方法2:连接OC,
利用对称
方法3:构造长方形
3.(湖北孝感) 如图,点A在双曲线
上,点B在双曲线 上,且AB∥x轴,C、
D在x轴上,若四边形ABCD为矩形,则它的
面积为 .
E
4(年陕西)如图,过y轴正半轴上的任意一点P,作x
轴的平行线,分别与反比例函数y=- 和y= 图象交于点
A和点B.若点C 是x轴上任意一点,连接AC、BC,则△ABC的面
积为 ( )
A.3 B.4
C.5 D.6
A
反比例函数中的面积问题
以形助数 用数解形
一个性质:反比例函数的面积不变性
多种思想:
数形结合
分类讨论
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考, 去发现,去总结。
