人教版数学九年级下册-27.2.1相似三角形的判定-课件(共26张ppt)
文档属性
| 名称 | 人教版数学九年级下册-27.2.1相似三角形的判定-课件(共26张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 15:16:26 | ||
图片预览



文档简介
人教版·九年级数学下册
新课导入
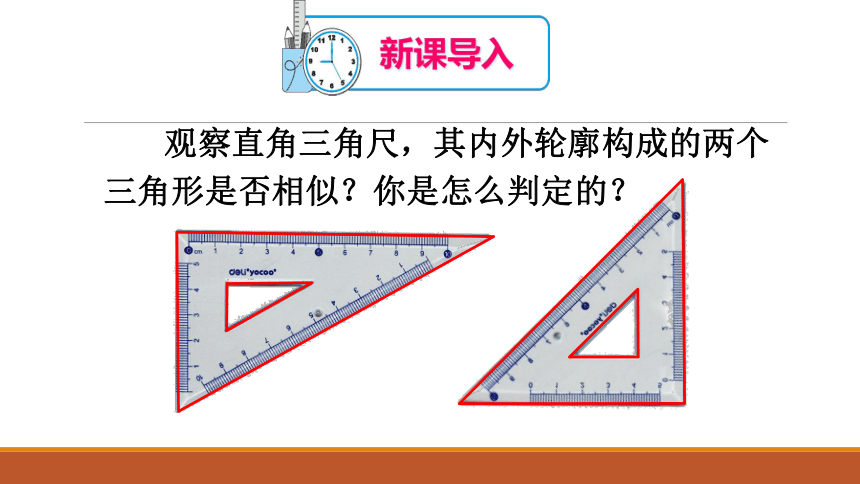
观察直角三角尺,其内外轮廓构成的两个三角形是否相似?你是怎么判定的?
1.知道两角分别相等的两个三角形相似;知道斜边、直角边成比例的两个直角三角形相似.
2.能证明结论“斜边、直角边成比例的两个直角三角形相似”.
3.能灵活选择适当的方法证明两个三角形相似.
学习目标
推进新课
相似三角形的判定定理
知识点1
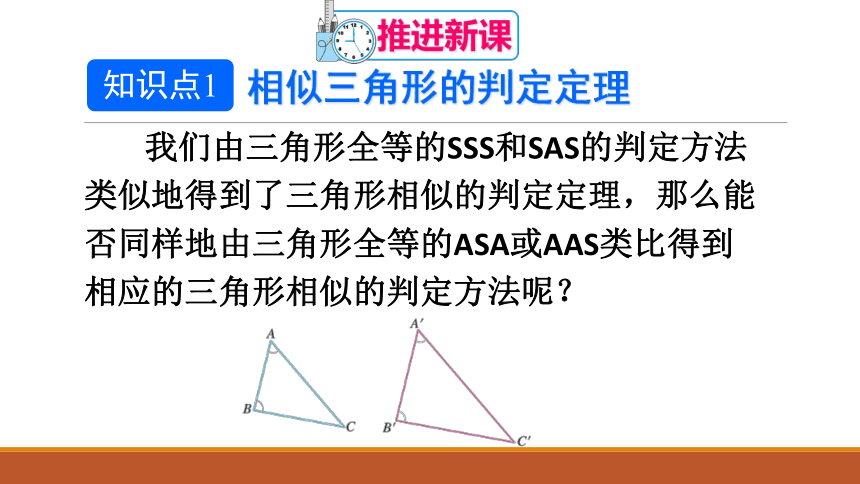
我们由三角形全等的SSS和SAS的判定方法类似地得到了三角形相似的判定定理,那么能否同样地由三角形全等的ASA或AAS类比得到相应的三角形相似的判定方法呢?
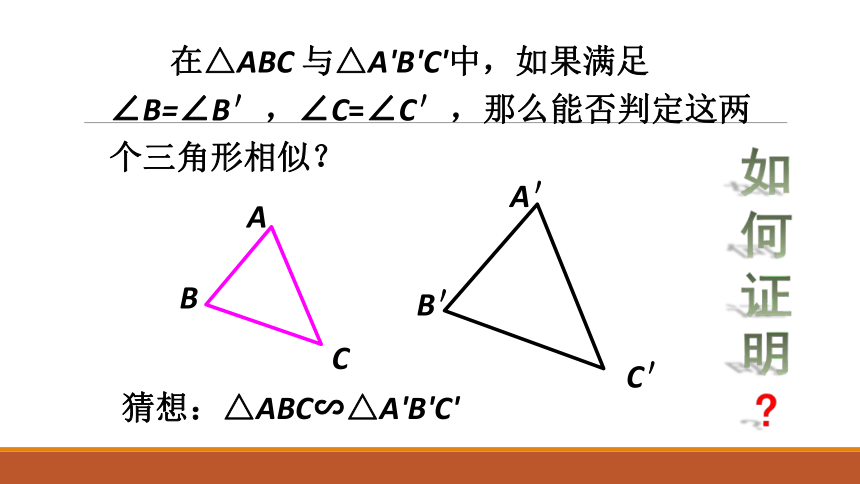
在△ABC 与△A'B'C'中,如果满足∠B=∠B',∠C=∠C',那么能否判定这两个三角形相似?
A'
B'
C'
B
A
C
猜想:△ABC∽△A'B'C'
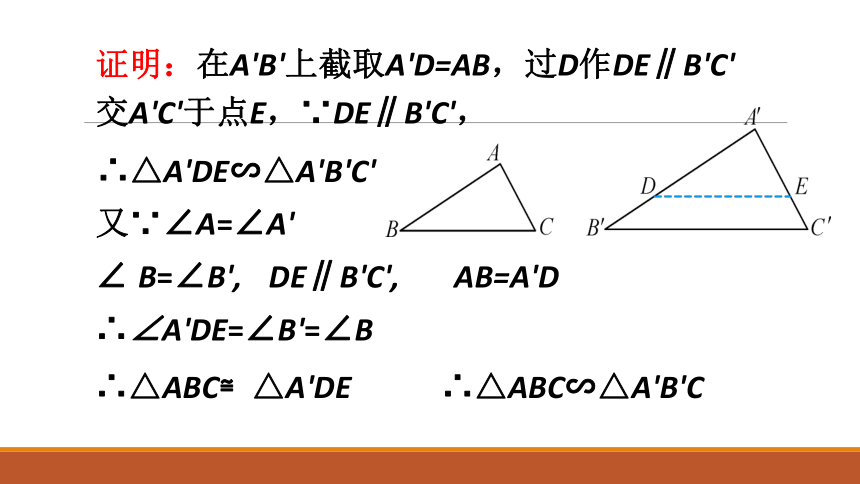
证明:在A'B'上截取A'D=AB,过D作DE∥B'C'
交A'C'于点E,∵DE∥B'C',
∴△A'DE∽△A'B'C'
又∵∠A=∠A'
∠ B=∠B',
DE∥B'C',
AB=A'D
∴∠A'DE=∠B'=∠B
∴△ABC≌△A'DE
∴△ABC∽△A'B'C
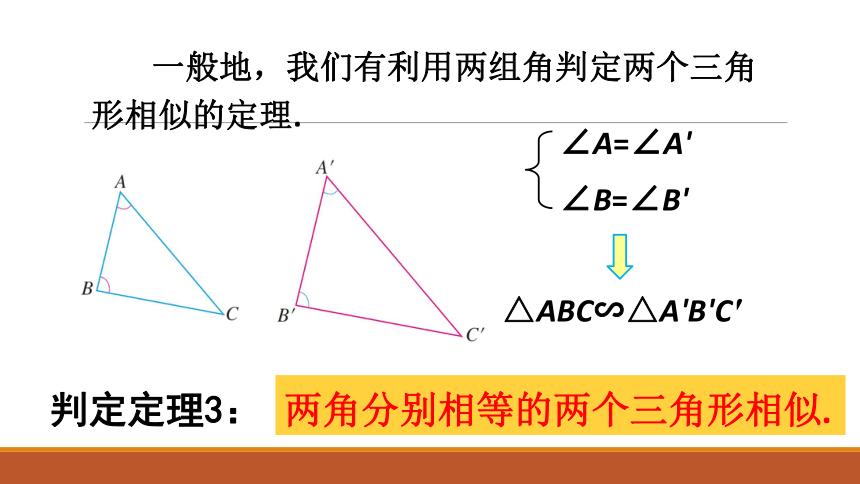
一般地,我们有利用两组角判定两个三角形相似的定理.
∠A=∠A'
∠B=∠B'
△ABC∽△A'B'C'
两角分别相等的两个三角形相似.
判定定理3:
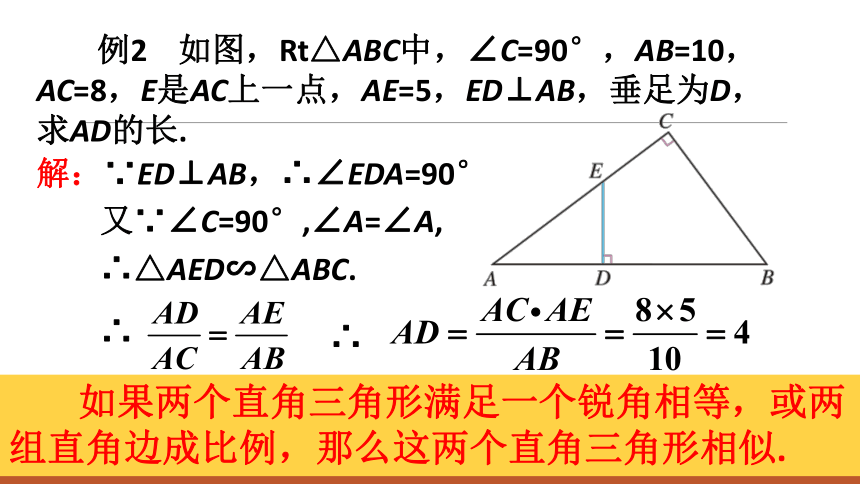
例2 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长.
解:∵ED⊥AB,∴∠EDA=90°
又∵∠C=90°,∠A=∠A,
∴△AED∽△ABC.
∴
∴
如果两个直角三角形满足一个锐角相等,或两组直角边成比例,那么这两个直角三角形相似.
一个判定定理
两角分别相等的两个三角形相似.
1
练习
1.如图,当 时,△ABC∽△AED(填写一个条件).
∠ADE=∠C(答案不唯一)
2.底角相等的两个等腰三角形是否相似?顶角相等的两个等腰三角形呢?证明你的结论.
解:(1)相似(2)相似
都符合两个角对应相等的两个三角形相似.
直角三角形相似判定定理
知识点2
思考
我们知道,两个直角三角形全等可以用“HL”来判定,那么满足斜边和一条直角边成比例的两个直角三角形相似吗?
如图,在Rt△ABC和Rt△A'B'C'中,∠C=90°,∠C'=90°, ,
求证Rt△ABC∽ Rt△A'B'C'.
分析:要证Rt△ABC∽ Rt△A'B'C'.
可设法证
若设
则只需证
证明:设 ,
则AB=kA'B',AC=kA'C'
由勾股定理得
∴
∴
∴
Rt△ABC∽ Rt△A'B'C'.
练习
1.如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高.求证:
(1)△ACD∽△ABC;(2)△CBD∽△ABC.
证明:(1)∵CD⊥AB,∴∠ADC=90°.
∴∠ADC=∠ACB,
在△ACD和△ABC中,
∵∠A=∠A,∠ADC=∠ACB,
∴△ACD∽△ABC.
(2)∵CD⊥AB,∴∠CDB=90°.
∴∠ACB=∠CDB.
在△CBD和△ABC中,
∵∠B=∠B,∠CDB=∠ACB,
∴△CBD∽△ABC.
2.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
C
A.P1 B.P2
C.P3 D.P4
随堂演练
基础巩固
1.从下面这些三角形中,选出相似的三角形.
①、⑤、⑥相似,③、④、⑧相似,②和⑦相似.
2.如图△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于点D,求证:△ABC∽△BDC.
证明:∵AB=AC,∠A=36°, BD平分∠ABC,
∴∠ABD=∠DBC=36°,∴∠A=∠DBC.
在△ABC和△BDC中,
∠A=∠DBC,∠C=∠C.
∴△ABC∽△BDC.
3.如图,AD是Rt△ABC的斜边上的高. 若AB=4 cm,BC=10 cm,求BD的长.
解:∵AD⊥BC,∠BAC=90°,
∴∠ADB=∠CAB.
∴△ABD∽△CBA,
即 ,
BD=1.6(cm).
∴
综合应用
4.如图,△ABC中,D在线段BC上,∠BAC=∠ADC,AC=8,BC=16.
(1)求证:△ABC∽△DAC;
(2)求CD的长.
(1)证明:∵∠BAC=∠ADC,∠C=∠C,
∴△ABC∽△DAC.
(2)解:∵△ABC∽△DAC,
∴
,即
∴CD=4.
课堂小结
两角分别相等的两个三角形相似.
如果两个直角三角形满足一个锐角相等,或两组直角边成比例,那么这两个直角三角形相似.
如图,M是Rt△ABC的斜边BC上异于B、C的一个定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )
A.1条 B.2条
C.3条 D.4条
C
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
新课导入
观察直角三角尺,其内外轮廓构成的两个三角形是否相似?你是怎么判定的?
1.知道两角分别相等的两个三角形相似;知道斜边、直角边成比例的两个直角三角形相似.
2.能证明结论“斜边、直角边成比例的两个直角三角形相似”.
3.能灵活选择适当的方法证明两个三角形相似.
学习目标
推进新课
相似三角形的判定定理
知识点1
我们由三角形全等的SSS和SAS的判定方法类似地得到了三角形相似的判定定理,那么能否同样地由三角形全等的ASA或AAS类比得到相应的三角形相似的判定方法呢?
在△ABC 与△A'B'C'中,如果满足∠B=∠B',∠C=∠C',那么能否判定这两个三角形相似?
A'
B'
C'
B
A
C
猜想:△ABC∽△A'B'C'
证明:在A'B'上截取A'D=AB,过D作DE∥B'C'
交A'C'于点E,∵DE∥B'C',
∴△A'DE∽△A'B'C'
又∵∠A=∠A'
∠ B=∠B',
DE∥B'C',
AB=A'D
∴∠A'DE=∠B'=∠B
∴△ABC≌△A'DE
∴△ABC∽△A'B'C
一般地,我们有利用两组角判定两个三角形相似的定理.
∠A=∠A'
∠B=∠B'
△ABC∽△A'B'C'
两角分别相等的两个三角形相似.
判定定理3:
例2 如图,Rt△ABC中,∠C=90°,AB=10,AC=8,E是AC上一点,AE=5,ED⊥AB,垂足为D,求AD的长.
解:∵ED⊥AB,∴∠EDA=90°
又∵∠C=90°,∠A=∠A,
∴△AED∽△ABC.
∴
∴
如果两个直角三角形满足一个锐角相等,或两组直角边成比例,那么这两个直角三角形相似.
一个判定定理
两角分别相等的两个三角形相似.
1
练习
1.如图,当 时,△ABC∽△AED(填写一个条件).
∠ADE=∠C(答案不唯一)
2.底角相等的两个等腰三角形是否相似?顶角相等的两个等腰三角形呢?证明你的结论.
解:(1)相似(2)相似
都符合两个角对应相等的两个三角形相似.
直角三角形相似判定定理
知识点2
思考
我们知道,两个直角三角形全等可以用“HL”来判定,那么满足斜边和一条直角边成比例的两个直角三角形相似吗?
如图,在Rt△ABC和Rt△A'B'C'中,∠C=90°,∠C'=90°, ,
求证Rt△ABC∽ Rt△A'B'C'.
分析:要证Rt△ABC∽ Rt△A'B'C'.
可设法证
若设
则只需证
证明:设 ,
则AB=kA'B',AC=kA'C'
由勾股定理得
∴
∴
∴
Rt△ABC∽ Rt△A'B'C'.
练习
1.如图,在Rt△ABC中,∠C=90°,CD是斜边AB上的高.求证:
(1)△ACD∽△ABC;(2)△CBD∽△ABC.
证明:(1)∵CD⊥AB,∴∠ADC=90°.
∴∠ADC=∠ACB,
在△ACD和△ABC中,
∵∠A=∠A,∠ADC=∠ACB,
∴△ACD∽△ABC.
(2)∵CD⊥AB,∴∠CDB=90°.
∴∠ACB=∠CDB.
在△CBD和△ABC中,
∵∠B=∠B,∠CDB=∠ACB,
∴△CBD∽△ABC.
2.如图,在方格纸中,△ABC和△EPD的顶点均在格点上,要使△ABC∽△EPD,则点P所在的格点为( )
C
A.P1 B.P2
C.P3 D.P4
随堂演练
基础巩固
1.从下面这些三角形中,选出相似的三角形.
①、⑤、⑥相似,③、④、⑧相似,②和⑦相似.
2.如图△ABC中,AB=AC,∠A=36°,∠ABC的平分线交AC于点D,求证:△ABC∽△BDC.
证明:∵AB=AC,∠A=36°, BD平分∠ABC,
∴∠ABD=∠DBC=36°,∴∠A=∠DBC.
在△ABC和△BDC中,
∠A=∠DBC,∠C=∠C.
∴△ABC∽△BDC.
3.如图,AD是Rt△ABC的斜边上的高. 若AB=4 cm,BC=10 cm,求BD的长.
解:∵AD⊥BC,∠BAC=90°,
∴∠ADB=∠CAB.
∴△ABD∽△CBA,
即 ,
BD=1.6(cm).
∴
综合应用
4.如图,△ABC中,D在线段BC上,∠BAC=∠ADC,AC=8,BC=16.
(1)求证:△ABC∽△DAC;
(2)求CD的长.
(1)证明:∵∠BAC=∠ADC,∠C=∠C,
∴△ABC∽△DAC.
(2)解:∵△ABC∽△DAC,
∴
,即
∴CD=4.
课堂小结
两角分别相等的两个三角形相似.
如果两个直角三角形满足一个锐角相等,或两组直角边成比例,那么这两个直角三角形相似.
如图,M是Rt△ABC的斜边BC上异于B、C的一个定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )
A.1条 B.2条
C.3条 D.4条
C
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
