人教版数学九年级下册-27.2.2相似三角形的性质-课件(共23张ppt)
文档属性
| 名称 | 人教版数学九年级下册-27.2.2相似三角形的性质-课件(共23张ppt) | 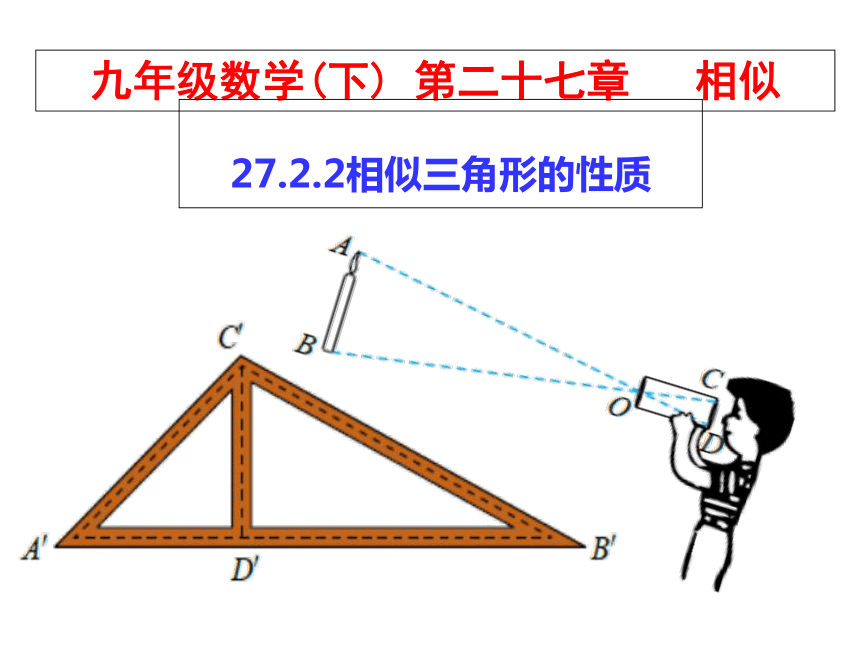 | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 12:07:35 | ||
图片预览





文档简介
九年级数学(下) 第二十七章 相似
27.2.2相似三角形的性质
1
理解并初步掌握相似三角形周长
的比等于相似比,面积的比等于
相似比的平方;
能用三角形的性质解决简单的
问题.
2
3
学习目标
理解:相似三角形的对应线段
的比都等于相似比;
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.
回顾与复习
A
B
C
A/
B/
C/
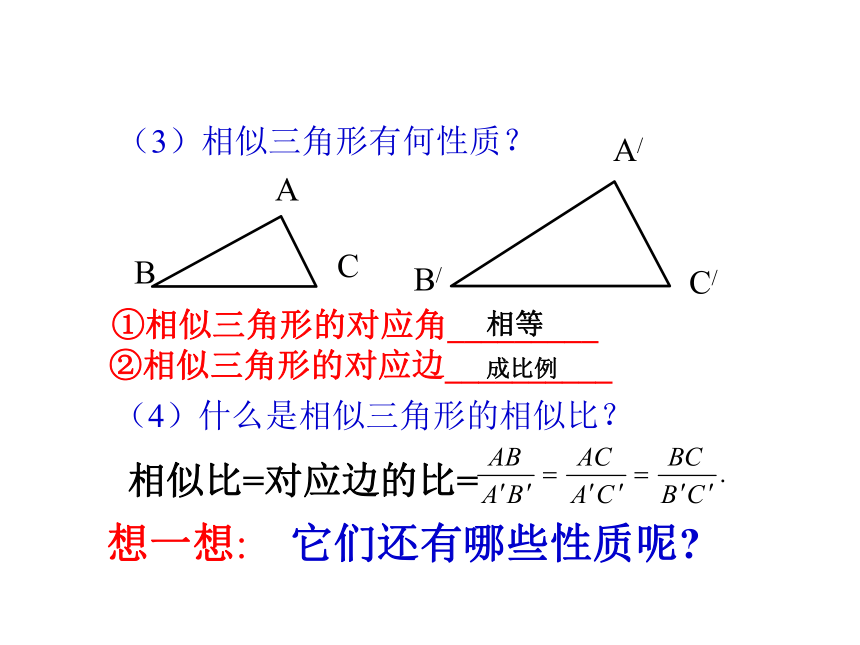
①相似三角形的对应角_________
②相似三角形的对应边__________
想一想: 它们还有哪些性质呢?
(3)相似三角形有何性质?
(4)什么是相似三角形的相似比?
相似比=对应边的比=
相等
成比例
一个三角形有三条重要线段:____ _____ _________
如果两个三角形相似,
那么这些对应线段有什么关系呢?
情境引入
高、中线、角平分线
F
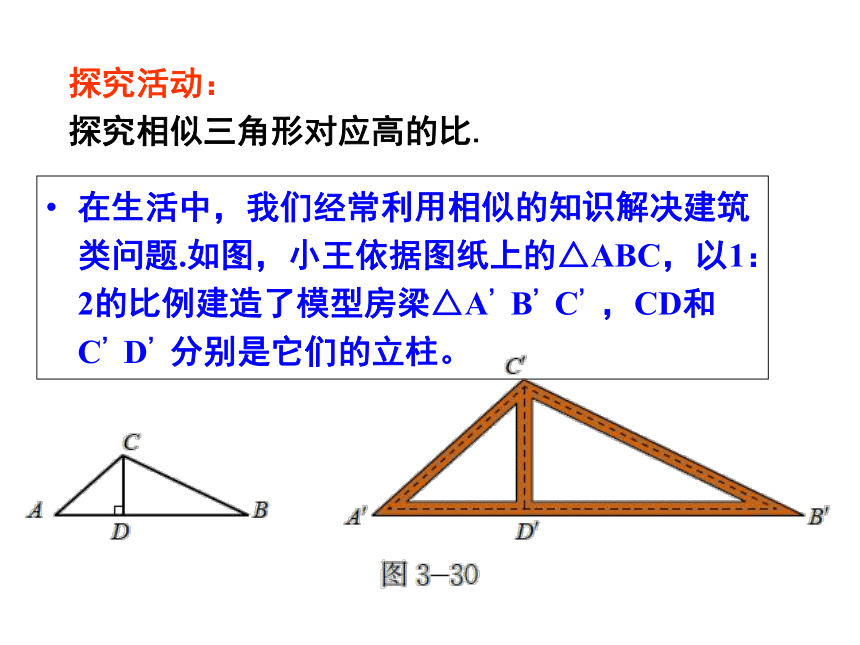
在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1:2的比例建造了模型房梁△A’B’C’,CD和C’D’分别是它们的立柱。
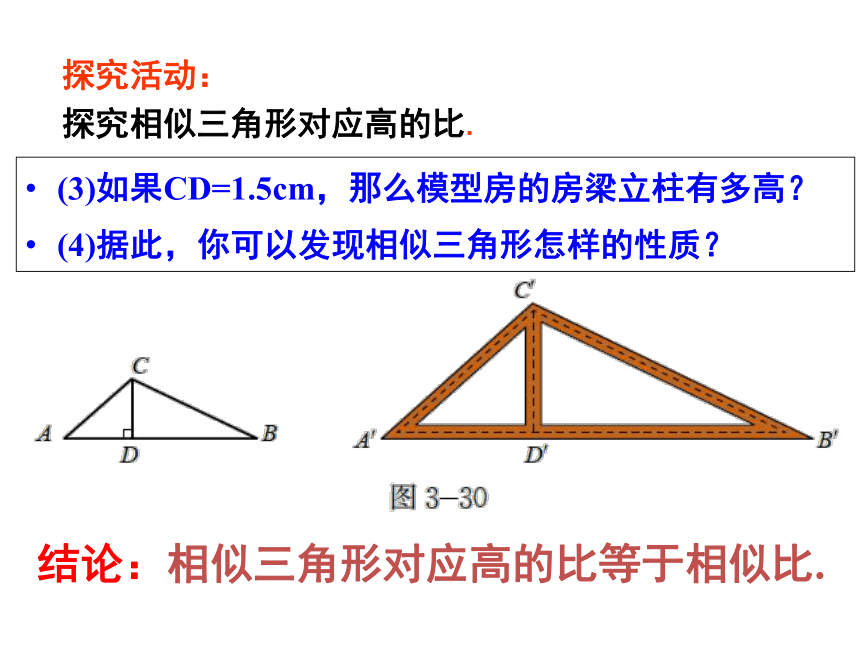
探究活动:
探究相似三角形对应高的比.
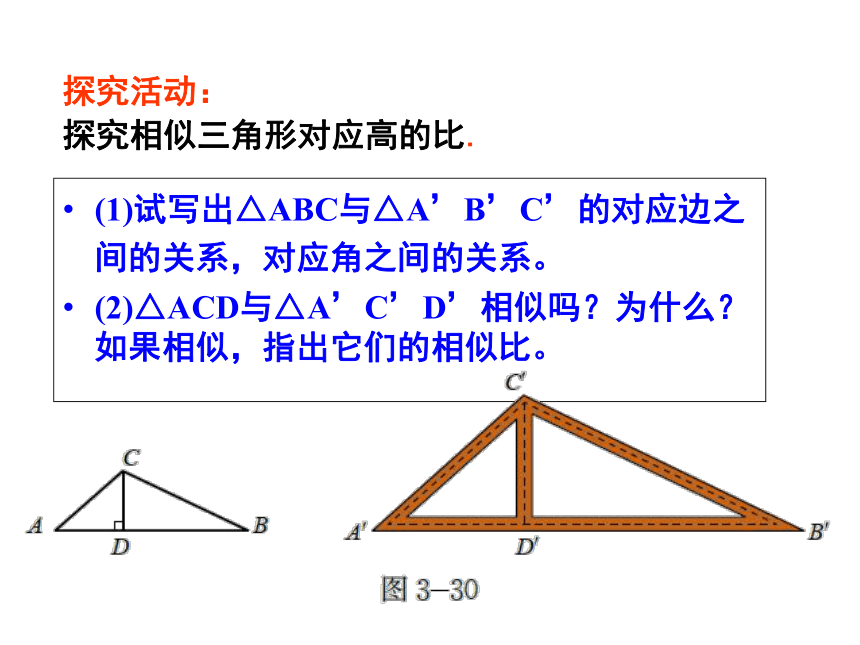
(1)试写出△ABC与△A’B’C’的对应边之间的关系,对应角之间的关系。
(2)△ACD与△A’C’D’相似吗?为什么?如果相似,指出它们的相似比。
探究活动:
探究相似三角形对应高的比.
(3)如果CD=1.5cm,那么模型房的房梁立柱有多高?
(4)据此,你可以发现相似三角形怎样的性质?
探究活动:
探究相似三角形对应高的比.
结论:相似三角形对应高的比等于相似比.
如图,∵△ABC∽△DEF,
∴∠B =∠E, ∠BAC=∠EDF.
又∵AM,DN分别是∠BAC和∠EDF的角平分线,
∴∠BAM=∠EDN,
∴△AMB∽△DNE
(两角对应相等的两个三角形相似),
已知△ABC ∽ △DEF, △ABC 与△DEF的相似比为K,AM、DN分别为三角形的角平分线,它们的对应角平分线的比是多少?
(相似三角形对应边成比例).
A
B
C
M
D
E
F
N
分组讨论,类似结论
结论:相似三角形对应角平分线的比等于相似比
如图,∵△ABC∽△DEF,
∴∠B =∠E,
结论:相似三角形对应中线的比等于相似比
A
B
C
M1
D
E
F
N1
又∵AM1,DN1分别是△ABC和△DEF的中线,
∴△AM1B∽△DN1E(两边对应成比例且夹角相等的两个三角形相似).
且∠B =∠E,
已知△ABC ∽ △DEF, △ABC 与△DEF的相似比为K,AM1、DN1分别为三角形的中线,它们的对应中线的比是多少?
填一填
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2∶ 3
2 ∶ 3
2.两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________.
1:4
1:4
3.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .
如图,AD是BC的高,点I,H在BC边上,点G在AC上,点F在AB上, BC=60cm,AD=40cm,四边形FGHI是正方形,
则
(1) △AFG与△ABC相似吗?为什么?
(2)求正方形FGHI的边长。
(1)∵四边形FGHI是正方形
∴ FG∥BC
∴ △AFG∽△ABC.
典例分析
如图,AD是BC的高,点I,H在BC边上,点G在AC上,点F在AB上, BC=60cm,AD=40cm,四边形FGHI是正方形,
则(1) △AFG与△ABG相似吗?为什么?
(2)求正方形FGHI的边长。
(2)∵ △AFG∽△ABC.
∴
设正方形FGHI的边长为xcm,
则AE=(40-x)cm,
解得,x=24.
所以正方形FGHI的边长为24cm.
典例分析
? 探索活动
如图,△ABC∽△A'B'C' ,相似比为2.
(1)请你写出图中所有成比例的线段;
(2)△ABC与△A'B'C' 的周长比是多少?
面积比呢?
D
D'
C′
A′
B′
C
A
B
如果△ABC∽△A'B'C',相似比为k,那么
因此
AB=k A'B',BC=kB'C',AC=kA'C '
从而
A
B
C
A'
B'
C'
得到:
相似三角形周长的比等于相似比
如图,△ABC∽△ A'B'D' ,
相似比为k,两个三角形周长比是多少?
如图,△ABC∽△A'B'C' ,相似比为k,那么你能求△ABC与△A'B'C' 的面积之比吗?
C
A
B
D
C ′
A′
B′
D′
相似三角形的面积比等于相似比的平方.
性质3:相似三角形的周长比等于相似比。
相似三角形的面积比等于相似比的平方。
C
A
B
D
C 1
A1
B1
D1
例题讲解 P38 例3
在△ABC和△DEF中,AB=2DE,AC=2DF,
∠A=∠D,若△ABC的边BC上的高为6,面积为 ,求△DEF的边EF上的高和面积.
解:在△ABC和△DEF中,
∵ AB=2DE,AC=2DF
∴
又 ∠D=∠A
∴ △DEF∽△ABC,相似比为
A
B
C
D
E
F
∵△ABC的边BC上的高为6,面积为
∴△DEF的边EF上的高为 ,
面积为
巩固练习
1.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的___倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的________倍。
2.两个相似三角形的一对对应边分别是35cm和14 cm,
(1)它们的周长差60cm,这两个三角形的周长分别是
。
(2)它们的面积之和是58cm2,这两个三角形的面积分别是_
_______ _。
25
10
100cm和40cm
50cm2和8cm2
巩固练习
3.已知梯形ABCD中,AD∥BC,对角线AC、BD交于点O,若△AOD的面积为4cm2, △BOC的面积为9cm2, 则梯形ABCD的面积为_________cm2
A
B
C
D
O
解:
∴△AOD∽△COB S△AOD:S△COB=4:9
∴OD:OB=2:3
∴S△AOD:S△AOB=2:3 S△COD:S△COB=2:3
∴S△AOB=6cm2 S△COD=6cm2
∴梯形ABCD的面积为25cm2
25
对应角相等
对应边成比例
对应高
对应中线
对应角平分线
周长
面积比等于相似比的平方
相似三角形的性质
的比等于相似比
作业:
1. 课本P39 2 P42 6、7。
2.课堂精练对应练习。
27.2.2相似三角形的性质
1
理解并初步掌握相似三角形周长
的比等于相似比,面积的比等于
相似比的平方;
能用三角形的性质解决简单的
问题.
2
3
学习目标
理解:相似三角形的对应线段
的比都等于相似比;
(1)什么叫相似三角形?
对应角相等、对应边成比例的三角形,叫做相似三角形.
(2)如何判定两个三角形相似?
①两个角对应相等;
②两边对应成比例,且夹角相等;
③三边对应成比例.
回顾与复习
A
B
C
A/
B/
C/
①相似三角形的对应角_________
②相似三角形的对应边__________
想一想: 它们还有哪些性质呢?
(3)相似三角形有何性质?
(4)什么是相似三角形的相似比?
相似比=对应边的比=
相等
成比例
一个三角形有三条重要线段:____ _____ _________
如果两个三角形相似,
那么这些对应线段有什么关系呢?
情境引入
高、中线、角平分线
F
在生活中,我们经常利用相似的知识解决建筑类问题.如图,小王依据图纸上的△ABC,以1:2的比例建造了模型房梁△A’B’C’,CD和C’D’分别是它们的立柱。
探究活动:
探究相似三角形对应高的比.
(1)试写出△ABC与△A’B’C’的对应边之间的关系,对应角之间的关系。
(2)△ACD与△A’C’D’相似吗?为什么?如果相似,指出它们的相似比。
探究活动:
探究相似三角形对应高的比.
(3)如果CD=1.5cm,那么模型房的房梁立柱有多高?
(4)据此,你可以发现相似三角形怎样的性质?
探究活动:
探究相似三角形对应高的比.
结论:相似三角形对应高的比等于相似比.
如图,∵△ABC∽△DEF,
∴∠B =∠E, ∠BAC=∠EDF.
又∵AM,DN分别是∠BAC和∠EDF的角平分线,
∴∠BAM=∠EDN,
∴△AMB∽△DNE
(两角对应相等的两个三角形相似),
已知△ABC ∽ △DEF, △ABC 与△DEF的相似比为K,AM、DN分别为三角形的角平分线,它们的对应角平分线的比是多少?
(相似三角形对应边成比例).
A
B
C
M
D
E
F
N
分组讨论,类似结论
结论:相似三角形对应角平分线的比等于相似比
如图,∵△ABC∽△DEF,
∴∠B =∠E,
结论:相似三角形对应中线的比等于相似比
A
B
C
M1
D
E
F
N1
又∵AM1,DN1分别是△ABC和△DEF的中线,
∴△AM1B∽△DN1E(两边对应成比例且夹角相等的两个三角形相似).
且∠B =∠E,
已知△ABC ∽ △DEF, △ABC 与△DEF的相似比为K,AM1、DN1分别为三角形的中线,它们的对应中线的比是多少?
填一填
1.相似三角形对应边的比为2∶3,那么相似比为_________,对应角的角平分线的比为______.
2∶ 3
2 ∶ 3
2.两个相似三角形的相似比为1:4, 则对应高的比为_________,对应角的角平分线的比为_________.
1:4
1:4
3.两个相似三角形对应中线的比为 ,
则相似比为______,对应高的比为______ .
如图,AD是BC的高,点I,H在BC边上,点G在AC上,点F在AB上, BC=60cm,AD=40cm,四边形FGHI是正方形,
则
(1) △AFG与△ABC相似吗?为什么?
(2)求正方形FGHI的边长。
(1)∵四边形FGHI是正方形
∴ FG∥BC
∴ △AFG∽△ABC.
典例分析
如图,AD是BC的高,点I,H在BC边上,点G在AC上,点F在AB上, BC=60cm,AD=40cm,四边形FGHI是正方形,
则(1) △AFG与△ABG相似吗?为什么?
(2)求正方形FGHI的边长。
(2)∵ △AFG∽△ABC.
∴
设正方形FGHI的边长为xcm,
则AE=(40-x)cm,
解得,x=24.
所以正方形FGHI的边长为24cm.
典例分析
? 探索活动
如图,△ABC∽△A'B'C' ,相似比为2.
(1)请你写出图中所有成比例的线段;
(2)△ABC与△A'B'C' 的周长比是多少?
面积比呢?
D
D'
C′
A′
B′
C
A
B
如果△ABC∽△A'B'C',相似比为k,那么
因此
AB=k A'B',BC=kB'C',AC=kA'C '
从而
A
B
C
A'
B'
C'
得到:
相似三角形周长的比等于相似比
如图,△ABC∽△ A'B'D' ,
相似比为k,两个三角形周长比是多少?
如图,△ABC∽△A'B'C' ,相似比为k,那么你能求△ABC与△A'B'C' 的面积之比吗?
C
A
B
D
C ′
A′
B′
D′
相似三角形的面积比等于相似比的平方.
性质3:相似三角形的周长比等于相似比。
相似三角形的面积比等于相似比的平方。
C
A
B
D
C 1
A1
B1
D1
例题讲解 P38 例3
在△ABC和△DEF中,AB=2DE,AC=2DF,
∠A=∠D,若△ABC的边BC上的高为6,面积为 ,求△DEF的边EF上的高和面积.
解:在△ABC和△DEF中,
∵ AB=2DE,AC=2DF
∴
又 ∠D=∠A
∴ △DEF∽△ABC,相似比为
A
B
C
D
E
F
∵△ABC的边BC上的高为6,面积为
∴△DEF的边EF上的高为 ,
面积为
巩固练习
1.把一个三角形变成和它相似的三角形,
(1)如果边长扩大为原来的5倍,那么面积扩大为原来的___倍。
(2)如果面积扩大为原来的100倍,那么边长扩大为原来的________倍。
2.两个相似三角形的一对对应边分别是35cm和14 cm,
(1)它们的周长差60cm,这两个三角形的周长分别是
。
(2)它们的面积之和是58cm2,这两个三角形的面积分别是_
_______ _。
25
10
100cm和40cm
50cm2和8cm2
巩固练习
3.已知梯形ABCD中,AD∥BC,对角线AC、BD交于点O,若△AOD的面积为4cm2, △BOC的面积为9cm2, 则梯形ABCD的面积为_________cm2
A
B
C
D
O
解:
∴△AOD∽△COB S△AOD:S△COB=4:9
∴OD:OB=2:3
∴S△AOD:S△AOB=2:3 S△COD:S△COB=2:3
∴S△AOB=6cm2 S△COD=6cm2
∴梯形ABCD的面积为25cm2
25
对应角相等
对应边成比例
对应高
对应中线
对应角平分线
周长
面积比等于相似比的平方
相似三角形的性质
的比等于相似比
作业:
1. 课本P39 2 P42 6、7。
2.课堂精练对应练习。
