人教版数学七年级上册 4.3.3余角与补角 课件(共25张ppt)
文档属性
| 名称 | 人教版数学七年级上册 4.3.3余角与补角 课件(共25张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 15:15:12 | ||
图片预览






文档简介
4.3.3
余角和补角
学习目标
掌握余角与补角定义和性质;
1
能熟练的求出一个角的余角和补角;
2
能利用性质灵活判断两个角是互余或者互补关系.
3
自主学习
1、仔细阅读教科书第137页
要求:①划出互余、互补的定义并找出关
键词
②完成学习卡中“知识积累”部分
时间:2分钟
概念学习
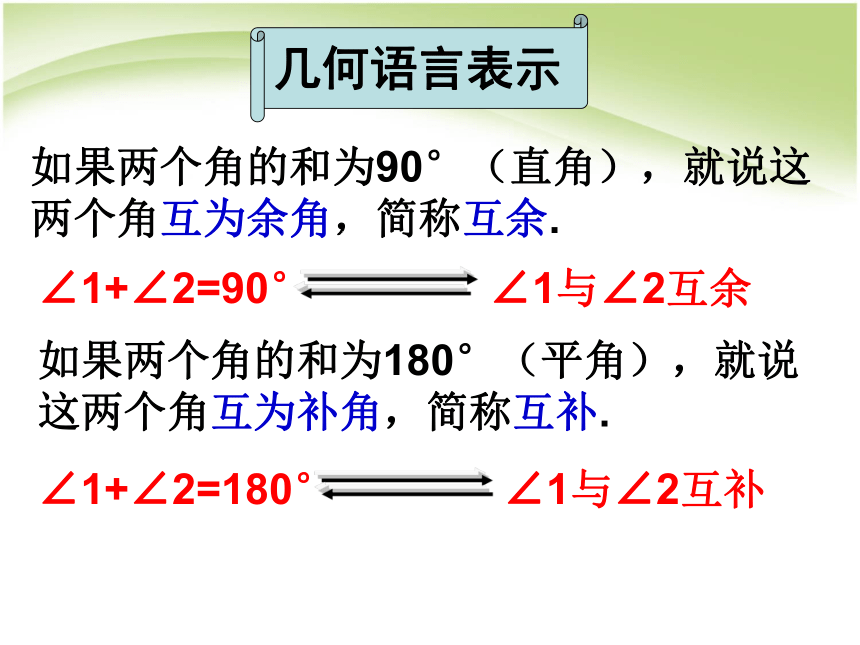
如果两个角的和为90°(直角),就说这
两个角互为余角,简称互余.
如果两个角的和为180°(平角),就说这两个角互为补角,简称互补.
如果两个角的和为90°(直角),就说这
两个角互为余角,简称互余.
∠1+∠2=90°
∠1与∠2互余
几何语言表示
如果两个角的和为180°(平角),就说这两个角互为补角,简称互补.
∠1+∠2=180°
∠1与∠2互补
检测学习
判断:
1、若??=55°,则它是余角.
(
)
2、若?1-?2=90°,则?1与?2互为补角.(
)
3、若?1+?2=180°,则?1与?2互为余角.(
)
4、若∠1+∠2+∠3
=90°(180°),则∠1、
∠2、∠3
互余(互补)
(
)
×
×
×
×
概念学习
如果两个角的和为90°(直角),就说这
两个角互为余角,简称互余.
如果两个角的和为180°(平角),就说这两个角互为补角,简称互补.
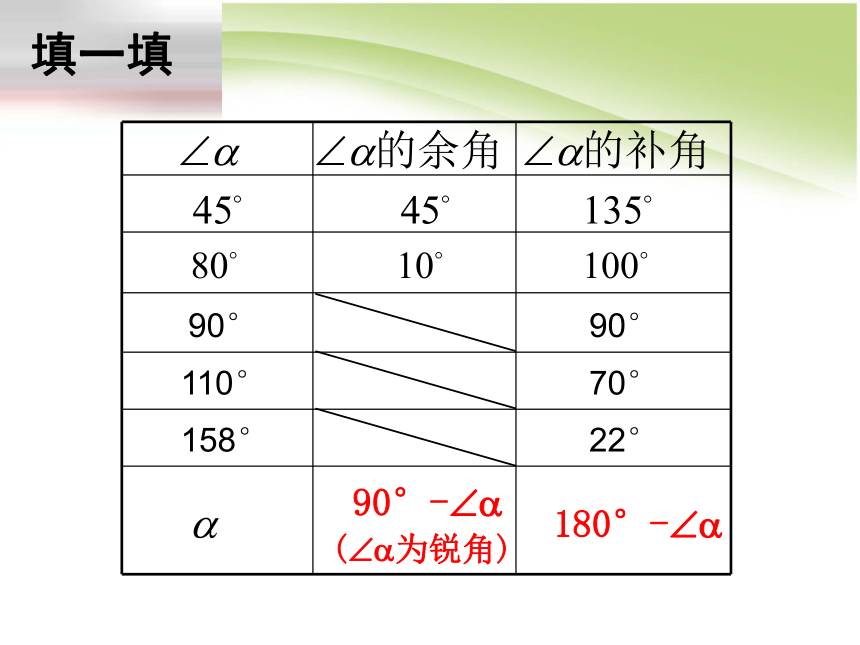
填一填
90°-??
180°-??
90°
90°
110°
70°
22°
158°
(??为锐角)
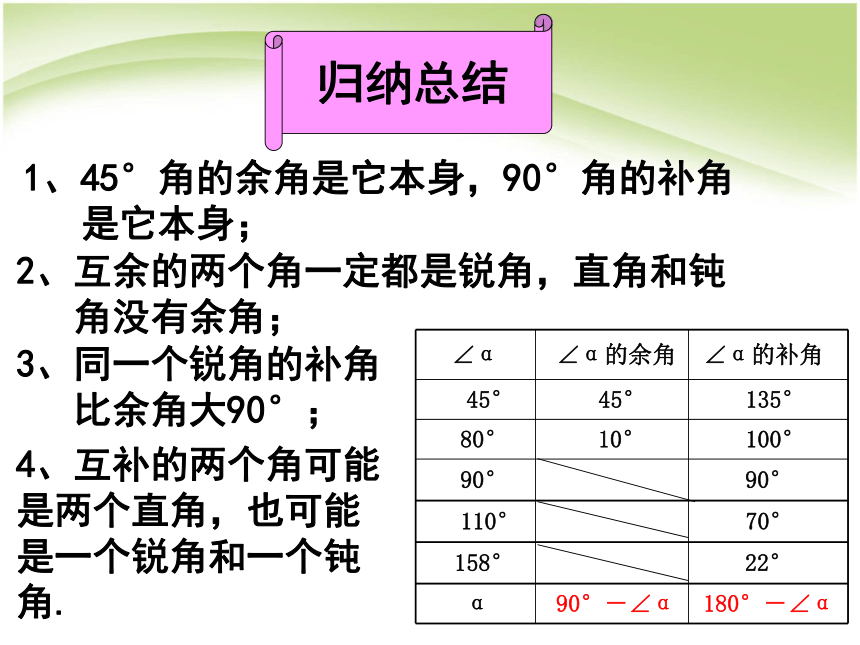
归纳总结
1、45°角的余角是它本身,90°角的补角
是它本身;
2、互余的两个角一定都是锐角,直角和钝
角没有余角;
3、同一个锐角的补角
比余角大90°;
4、互补的两个角可能
是两个直角,也可能
是一个锐角和一个钝角.
∠α
∠α的余角
∠α的补角
45°
45°
135°
80°
10°
100°
90°
90°
110°
70°
158°
22°
α
90°-∠α
180°-∠α
探究
同角的余角相等
1、若∠α=40°,则∠α的余角为________.
2、若∠2是∠1的余角,则∠2=__________;
∠3也是∠1的余角,则∠3=___________.
想一想:
第2题中的∠2和∠3有什么数量关系?
∠2=∠3
50°
90°-∠1
90°-∠1
探究
同角的补角相等
1、若∠α=40°,则∠α的补角为________.
2、若∠2是∠1的补角,则∠2=__________;
∠3也是∠1的补角,则∠3=__________.
想一想:
第2题中的∠2和∠3有什么数量关系?
∠2=∠3
140°
180°-∠1
180°-∠1
探究
等角的余角相等
1、若∠α=25°,则∠α的余角为_________.
2、若∠1与∠2互余,则
∠2=___________;
若∠3与∠4互余,则
∠3=___________;
想一想:
若第2题中的∠1=∠4,则∠2与∠3有什么数量关系?
∠2=∠3
65°
90°-
∠1
90°-
∠4
探究
等角的补角相等
1、若∠α=25°,则∠α的补角为_________.
2、若∠1与∠2互补,则
∠2=___________;
若∠3与∠4互补,则
∠3=___________;
想一想:
若第2题中的∠1=∠4,则∠2与∠3有什么数量关系?
∠2=∠3
155°
180°-
∠1
180°-
∠4
归纳总结
同角的余角相等.
同角的补角相等.
等角的余角相等.
等角的余角相等.
归纳总结
同角(等角)的余角相等.
同角(等角)的补角相等.
1、填空:
⑴70°的余角是
,补角是
.
⑵已知??的补角是125°,则??=
.
⑶已知?1的补角是115°,则?1的余角是_____________.
⑷若?1与?2互补,?2与?3互补,?1=50°,则?3=________.
⑸若?1+?2=90°,?3+?4=90°,?1=?4=40°,则?3=_________;
依据是_____________________.
20°
110°
55°
25°
50°
50°
等角的余角相等
学习了新知识,我们来检测一下吧!
恭喜你,过关啦!赶快进入下一关吧!
2、下列说法中正确的是(
)
A、一个锐角的余角一定比这个角大.
B、钝角没有余角,但一定有补角.
C、一个角的补角必定是钝角.
D、如果两个互补,那么这两个角中,必
定一个是锐角,另一个是钝角.
B
3、如图∠AOC=
∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
∠2
,∠4
∠3
,∠1
你真棒,又过了一关,继续加油哦!
B
A
O
C
1、如图两堵墙围一个角
,但人不能进入围墙,我们如何去测量这个角的大小呢?
动动脑
练一练
练一练
2、一个角的补角是它的余角的4倍,求这个
角的余角是多少度?
解:设这个角的度数为
,则依题意得
答:这个角的余角的度数为
另解:设这个角的余角的度数为
,
则它的补角可设为
答:这个角的余角的度数为
3、如图,已知A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC,则
⑴∠DOE多少度?
⑵∠2与∠3是什么关系?
⑶图中共有几对互余的角?
1
2
3
4
∠DOE=90°
∠2与∠3互余
∠2与∠3
∠2与∠4
∠1与∠3
∠1与∠4
谈一谈
这节课,你收获了什么?
互余
互补
两角间的数量
关系
对应
图形
性质
同角或等角的
余角相等
同角或等角的
补角相等
小结
作
业
必做:1、课本P139习题4.3
6、7
2、《新课程》P88~P89
选做:课本P140习题4.3
11、13
再见
余角和补角
学习目标
掌握余角与补角定义和性质;
1
能熟练的求出一个角的余角和补角;
2
能利用性质灵活判断两个角是互余或者互补关系.
3
自主学习
1、仔细阅读教科书第137页
要求:①划出互余、互补的定义并找出关
键词
②完成学习卡中“知识积累”部分
时间:2分钟
概念学习
如果两个角的和为90°(直角),就说这
两个角互为余角,简称互余.
如果两个角的和为180°(平角),就说这两个角互为补角,简称互补.
如果两个角的和为90°(直角),就说这
两个角互为余角,简称互余.
∠1+∠2=90°
∠1与∠2互余
几何语言表示
如果两个角的和为180°(平角),就说这两个角互为补角,简称互补.
∠1+∠2=180°
∠1与∠2互补
检测学习
判断:
1、若??=55°,则它是余角.
(
)
2、若?1-?2=90°,则?1与?2互为补角.(
)
3、若?1+?2=180°,则?1与?2互为余角.(
)
4、若∠1+∠2+∠3
=90°(180°),则∠1、
∠2、∠3
互余(互补)
(
)
×
×
×
×
概念学习
如果两个角的和为90°(直角),就说这
两个角互为余角,简称互余.
如果两个角的和为180°(平角),就说这两个角互为补角,简称互补.
填一填
90°-??
180°-??
90°
90°
110°
70°
22°
158°
(??为锐角)
归纳总结
1、45°角的余角是它本身,90°角的补角
是它本身;
2、互余的两个角一定都是锐角,直角和钝
角没有余角;
3、同一个锐角的补角
比余角大90°;
4、互补的两个角可能
是两个直角,也可能
是一个锐角和一个钝角.
∠α
∠α的余角
∠α的补角
45°
45°
135°
80°
10°
100°
90°
90°
110°
70°
158°
22°
α
90°-∠α
180°-∠α
探究
同角的余角相等
1、若∠α=40°,则∠α的余角为________.
2、若∠2是∠1的余角,则∠2=__________;
∠3也是∠1的余角,则∠3=___________.
想一想:
第2题中的∠2和∠3有什么数量关系?
∠2=∠3
50°
90°-∠1
90°-∠1
探究
同角的补角相等
1、若∠α=40°,则∠α的补角为________.
2、若∠2是∠1的补角,则∠2=__________;
∠3也是∠1的补角,则∠3=__________.
想一想:
第2题中的∠2和∠3有什么数量关系?
∠2=∠3
140°
180°-∠1
180°-∠1
探究
等角的余角相等
1、若∠α=25°,则∠α的余角为_________.
2、若∠1与∠2互余,则
∠2=___________;
若∠3与∠4互余,则
∠3=___________;
想一想:
若第2题中的∠1=∠4,则∠2与∠3有什么数量关系?
∠2=∠3
65°
90°-
∠1
90°-
∠4
探究
等角的补角相等
1、若∠α=25°,则∠α的补角为_________.
2、若∠1与∠2互补,则
∠2=___________;
若∠3与∠4互补,则
∠3=___________;
想一想:
若第2题中的∠1=∠4,则∠2与∠3有什么数量关系?
∠2=∠3
155°
180°-
∠1
180°-
∠4
归纳总结
同角的余角相等.
同角的补角相等.
等角的余角相等.
等角的余角相等.
归纳总结
同角(等角)的余角相等.
同角(等角)的补角相等.
1、填空:
⑴70°的余角是
,补角是
.
⑵已知??的补角是125°,则??=
.
⑶已知?1的补角是115°,则?1的余角是_____________.
⑷若?1与?2互补,?2与?3互补,?1=50°,则?3=________.
⑸若?1+?2=90°,?3+?4=90°,?1=?4=40°,则?3=_________;
依据是_____________________.
20°
110°
55°
25°
50°
50°
等角的余角相等
学习了新知识,我们来检测一下吧!
恭喜你,过关啦!赶快进入下一关吧!
2、下列说法中正确的是(
)
A、一个锐角的余角一定比这个角大.
B、钝角没有余角,但一定有补角.
C、一个角的补角必定是钝角.
D、如果两个互补,那么这两个角中,必
定一个是锐角,另一个是钝角.
B
3、如图∠AOC=
∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
∠2
,∠4
∠3
,∠1
你真棒,又过了一关,继续加油哦!
B
A
O
C
1、如图两堵墙围一个角
,但人不能进入围墙,我们如何去测量这个角的大小呢?
动动脑
练一练
练一练
2、一个角的补角是它的余角的4倍,求这个
角的余角是多少度?
解:设这个角的度数为
,则依题意得
答:这个角的余角的度数为
另解:设这个角的余角的度数为
,
则它的补角可设为
答:这个角的余角的度数为
3、如图,已知A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和∠BOC,则
⑴∠DOE多少度?
⑵∠2与∠3是什么关系?
⑶图中共有几对互余的角?
1
2
3
4
∠DOE=90°
∠2与∠3互余
∠2与∠3
∠2与∠4
∠1与∠3
∠1与∠4
谈一谈
这节课,你收获了什么?
互余
互补
两角间的数量
关系
对应
图形
性质
同角或等角的
余角相等
同角或等角的
补角相等
小结
作
业
必做:1、课本P139习题4.3
6、7
2、《新课程》P88~P89
选做:课本P140习题4.3
11、13
再见
