人教版数学七年级上册2.2.1整式的加减-合并同类项 课件(共17张ppt)
文档属性
| 名称 | 人教版数学七年级上册2.2.1整式的加减-合并同类项 课件(共17张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 12:10:58 | ||
图片预览






文档简介
我们常常把具有相同特征的事物归为一类.
捐款结束,班干部要留下来清点班级捐款总数,假如你是班干部,面对这一堆不同面值的钱,你如何数?
创设情境,问题导入
合作交流,探究新知
问题1:多项式3x2y-4y3-3-5x2y+5有那些项,它们分别是什么?
探究一:同类项的概念
3x2y -4y3 -3 -5x2y 5
请用合理的方式对上述单项式分类?
3x2y 和 -5x2y , -4y3 , -3和 5
2.2 整式的加减
第1课时合并同类项
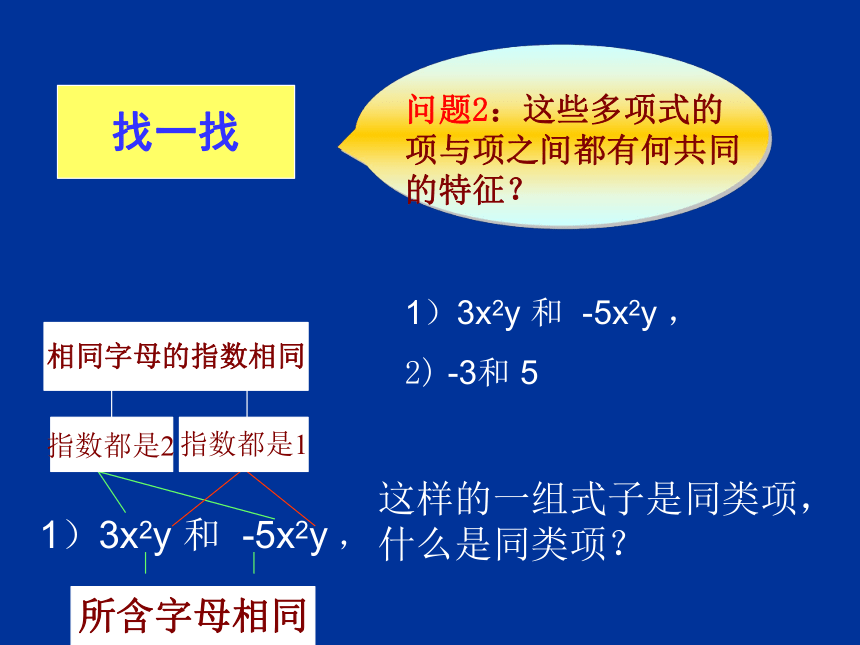
问题2:这些多项式的项与项之间都有何共同的特征?
找一找
这样的一组式子是同类项,
什么是同类项?
指数都是2
指数都是1
相同字母的指数相同
所含字母相同
1)3x2y 和 -5x2y ,
2) -3和 5
1)3x2y 和 -5x2y ,
同类项定义: 多项式中,所含字母相同,并且相同字母的指数也相同的项叫做同类项。几个常数项也是同类项。
两同
1.说出下列各题的两项是不是同类项?为什么?
(1)a3与b3 ( )
(2)-4x2y与4xy2 ( )
(3)3.5abc与0.5acb ( )
(4)-2 与 4 ( )
两 同:所含字母相同;相同字母的指数相同。
辨一辨
两无关:与系数无关;与字母的顺序无关。
我们规定:所有的常数项都是同类项
活动一
问题3:通过上面的练习,同类项有哪些同?与什么无关?
探究二:合并同类项
38 *10 + 32*10 = (38+32) *10
合作学习: 1、类比上面式子的运算,合并同类项 (1) 7x + 3x = (2) 4 x2 - 2 x2 = (3) 5ab2 - 13ab2= (4) –9x2y3 + 5x2y3=
10x
2x2
-8ab2
-4x2y3
38t+32t=___________
(38+32)t
问题4:想一想,如何合并同类项?
合并同类项法则:
同类项的系数相加,所得结果作为
系数,字母和字母的指数不变.
1.下列各题的结果是否正确?指出错误的地方.
(3)3a+2b=5ab
(4)-7ab+7ba=0
(√)
(×)
(×)
(×)
(1)b3+b3=2b6
(2)-5x3+2x3= -3
1、一变两不变
2、只有同类项才可合并
解:4x2 - 8x + 5-3x2 + 6x -4
~~~ ~~~
=(4x2-3x2)
= x2
(-8x+6x)
(5-4)
-2x
+1
2.合并多项式中4x2-8x+5-3x2+6x-4中的同类项。
— ——
+ +
一找
二移
三并
问题5:如何合并多项式中同类项
1、找出同类项
用不同的线标记出各组同类项,注意每一项的符号。
2、把同类项移在一起
用括号将同类项结合,括号间用加号连接。
3、合并同类项
系数相加,字母及字母的指数不变 。
要记住呀!!
2.合并多项式3x2y-4y3-3-5x2y+5的同类项?
深化理解,强化练习
基础训练:
1.下列各组是不是同类项?为什么?
(1) 4abc 与 4ab
(2) -5 m2 n3 与 2n3 m2
(3) -0.3 x2 y 与 y x2
1、若5x2 y与 x m yn同类项,则m=( ) n=( )
若5x2 y与 x m yn的和是单项式,m=( ),
n=( )
能力提升
2
1
2
1
2.若-5a3bm+1与8an+1b2是同类项,求(m-n)100的值。
解:由同类项的定义知:m+1=2,n+1=3;解得m=1,n=2
∴(m-n)100=(1-2)100=(-1)100=1
答:当m=1,n=2时,(m-n)100=1。
我最大的收获……
表现较好的方面我……
我学会了哪些知识……
我还有哪些疑惑……
小结
合并同类项
法则
(1) ______________相加
作为结果的系数。
(2) 不变。
同 类 项
定义
所含_____相同,并且 ______ 的______ 也 相同的项, 叫做同类项。
几个常数项也是_______。
字母
相同字母
指数
同类项
同类项的系数
字母与字母的指数
两同两无关
一变两不变
小 结
1
2
捐款结束,班干部要留下来清点班级捐款总数,假如你是班干部,面对这一堆不同面值的钱,你如何数?
创设情境,问题导入
合作交流,探究新知
问题1:多项式3x2y-4y3-3-5x2y+5有那些项,它们分别是什么?
探究一:同类项的概念
3x2y -4y3 -3 -5x2y 5
请用合理的方式对上述单项式分类?
3x2y 和 -5x2y , -4y3 , -3和 5
2.2 整式的加减
第1课时合并同类项
问题2:这些多项式的项与项之间都有何共同的特征?
找一找
这样的一组式子是同类项,
什么是同类项?
指数都是2
指数都是1
相同字母的指数相同
所含字母相同
1)3x2y 和 -5x2y ,
2) -3和 5
1)3x2y 和 -5x2y ,
同类项定义: 多项式中,所含字母相同,并且相同字母的指数也相同的项叫做同类项。几个常数项也是同类项。
两同
1.说出下列各题的两项是不是同类项?为什么?
(1)a3与b3 ( )
(2)-4x2y与4xy2 ( )
(3)3.5abc与0.5acb ( )
(4)-2 与 4 ( )
两 同:所含字母相同;相同字母的指数相同。
辨一辨
两无关:与系数无关;与字母的顺序无关。
我们规定:所有的常数项都是同类项
活动一
问题3:通过上面的练习,同类项有哪些同?与什么无关?
探究二:合并同类项
38 *10 + 32*10 = (38+32) *10
合作学习: 1、类比上面式子的运算,合并同类项 (1) 7x + 3x = (2) 4 x2 - 2 x2 = (3) 5ab2 - 13ab2= (4) –9x2y3 + 5x2y3=
10x
2x2
-8ab2
-4x2y3
38t+32t=___________
(38+32)t
问题4:想一想,如何合并同类项?
合并同类项法则:
同类项的系数相加,所得结果作为
系数,字母和字母的指数不变.
1.下列各题的结果是否正确?指出错误的地方.
(3)3a+2b=5ab
(4)-7ab+7ba=0
(√)
(×)
(×)
(×)
(1)b3+b3=2b6
(2)-5x3+2x3= -3
1、一变两不变
2、只有同类项才可合并
解:4x2 - 8x + 5-3x2 + 6x -4
~~~ ~~~
=(4x2-3x2)
= x2
(-8x+6x)
(5-4)
-2x
+1
2.合并多项式中4x2-8x+5-3x2+6x-4中的同类项。
— ——
+ +
一找
二移
三并
问题5:如何合并多项式中同类项
1、找出同类项
用不同的线标记出各组同类项,注意每一项的符号。
2、把同类项移在一起
用括号将同类项结合,括号间用加号连接。
3、合并同类项
系数相加,字母及字母的指数不变 。
要记住呀!!
2.合并多项式3x2y-4y3-3-5x2y+5的同类项?
深化理解,强化练习
基础训练:
1.下列各组是不是同类项?为什么?
(1) 4abc 与 4ab
(2) -5 m2 n3 与 2n3 m2
(3) -0.3 x2 y 与 y x2
1、若5x2 y与 x m yn同类项,则m=( ) n=( )
若5x2 y与 x m yn的和是单项式,m=( ),
n=( )
能力提升
2
1
2
1
2.若-5a3bm+1与8an+1b2是同类项,求(m-n)100的值。
解:由同类项的定义知:m+1=2,n+1=3;解得m=1,n=2
∴(m-n)100=(1-2)100=(-1)100=1
答:当m=1,n=2时,(m-n)100=1。
我最大的收获……
表现较好的方面我……
我学会了哪些知识……
我还有哪些疑惑……
小结
合并同类项
法则
(1) ______________相加
作为结果的系数。
(2) 不变。
同 类 项
定义
所含_____相同,并且 ______ 的______ 也 相同的项, 叫做同类项。
几个常数项也是_______。
字母
相同字母
指数
同类项
同类项的系数
字母与字母的指数
两同两无关
一变两不变
小 结
1
2
