人教版数学七年级上册3.1.1一元一次方程 课件(共19张ppt)
文档属性
| 名称 | 人教版数学七年级上册3.1.1一元一次方程 课件(共19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-13 00:00:00 | ||
图片预览






文档简介
3.1.1一元一次方程
教学目标:1、理解并掌握一元一次方程的概念,能正确的判断一元一次方程。
2、能将实际问题抽象为数学问题,并通过方程解决问题。
重点:理解一元一次方程的概念,辨识一元一次方程
难点:一元一次方程的理解,根据实际问题列一元一次方程
法国数学家笛卡尔,最早提出用x,y,z等字母表示未知数,我国古代用“天元、地元、人元、物元”等表示未知数
等式
方程
回顾方程
1+2=3
5=7-2
3+b=2b+1
4+x=7
0.7x=1400
2x-2=6
1、像这种用等号“=”来表示相等关系的式子,叫 。
2、像这样含有未知数的等式叫做 。
判断方程的两个关键要素:
①有未知数 ②是等式
请大家观察左边的这些式子,看看它们有什么共同的特征?
判断下列各式哪些是方程?
×
√
×
×
√
①5x +3y-6x =37( ) ②4x -7( )
③5x ≥ 3 ( ) ④ 6x ?+x -2=0 ( )
⑤1+2=3 ( ) ⑥ ( )
√
回顾方程
合作交流,探索新知
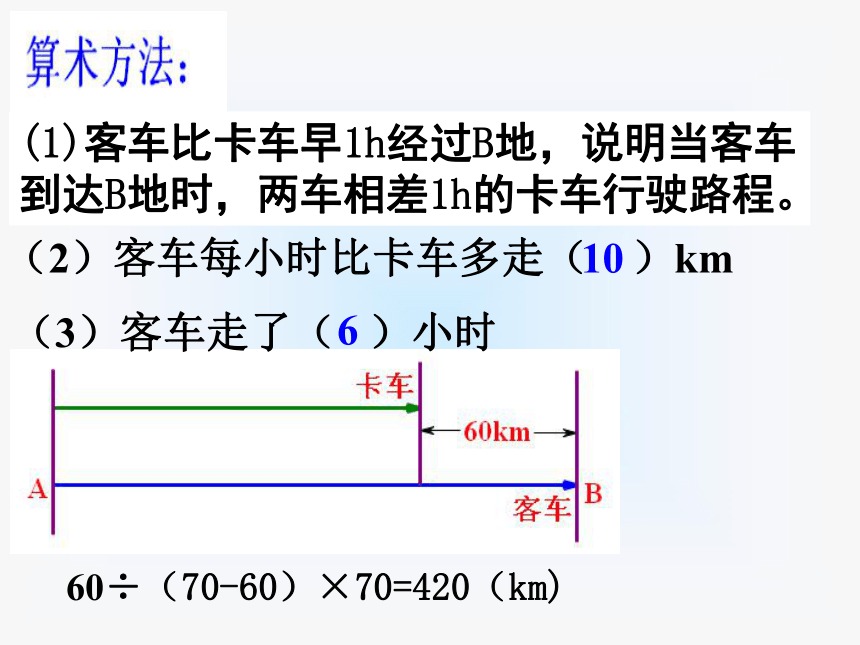
问题:一辆客车和一辆卡车同时从A地出发,沿同一条公路同方向行驶,客车的行驶速度是70km/h,卡车的行驶是60km/h,客车比卡车早1h经过B地。A、B两地的路程是多少?
你会用算术方法解决这个问题吗?列算式试试。
(1)客车比卡车早1h经过B地,说明当客车到达B地时,两车相差1h的卡车行驶路程。
(2)客车每小时比卡车多走( )km
(3)客车走了( )小时
10
6
60÷(70-60)×70=420(km)
x
x
思考
算术方法: 列出的算式表示解题的计算过程,其中只能用已知数.对于较复杂的问题,列算式比较困难.
列方程(代数方法): 方程是根据题中的等量关系列出的等式.其中既含已知数,又含未知数.使问题的已知量与未知量之间的关系很容易表示,解决问题就比较方便.
所以,从算术到方程是数学的进步
小试牛刀
例1.根据下列问题,设未知数并列方程(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少cm?
列方程: 4 =24
解:如设正方形的边长为 cm,
x
x
一显身手:
解:设x月后这台计算机的使用时间达到 2450 小时。
根据题意得:1700 + 150x = 2450
(2)一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间达到规定的检修时间2450小时?
已用的时间+还可用时间150x小时=规定的检测时间2450小时.
相等关系:
我探究我发现
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
列方程 0.52x-(1-0.52)x=80
解:设这个学校有X人,那么女生人数( ) ,
男生人数为( )。
等量关系:女生比男生多80人。
0.52x
(1-0.52)x
4x=24,
1700+150x=2450,
0.52x-(1-0.52)x=80
③等号两边都是整式;
①都只含有一个(一种)未知数;
②未知数的次数都是1;
④一次项系数不能为零。
下面的三个方程:
有什么共同点?
一元一次方程:
只含有一个未知数(元),未知
数的次数都是1,等号两边都是整式,这样的方程叫一元一次方程。
我探究,我发现
小试身手
注意:一元一次方程中,只含有一个未知数,且未知数的次数都是1,等号两边都是整式。
接下来,拟人情境动画:判断下列成员是否一元一次方程家族成员?能否进入家庭聚会之门?若不行,请说明理由。
第一组① 5x = 0 ②1+3x ③ y2 = 4+y
④ 3m+2 = 1-n ⑤ x = 6 ⑥ +2x=5
第二组:若2x b+1 = 5, (a-1)x2+x = 3也想参加聚会,a、b满足什么条件?
归纳:书P79
像之前那样在解答实际问题时,为了方便思考,利用方程的方法去解答,这就是方程的思想。
总结反思:
1.设:恰当的设出未知数,用字母X表示问题中的未知量
3.列:利用实际问题中的相等关系列出方程
2.找:寻找实际问题中的相等关系
关键
列出一元一次方程的一般步骤:
一种方法——列方程解决实际问题的方法;
两个概念——方程、一元一次方程。
1、通过本节的学习你有什么收获?
2、在这部分学习中,你还有什么困难?
作 业
1、必做题:P83页习题3.1 第一题
2、选做题:天平的两个盘A、B内分别盛有51g、45g盐,设应该从盘A内拿出多少g盐放到盘B内,才能使两者所盛盐的质量相等?
教学目标:1、理解并掌握一元一次方程的概念,能正确的判断一元一次方程。
2、能将实际问题抽象为数学问题,并通过方程解决问题。
重点:理解一元一次方程的概念,辨识一元一次方程
难点:一元一次方程的理解,根据实际问题列一元一次方程
法国数学家笛卡尔,最早提出用x,y,z等字母表示未知数,我国古代用“天元、地元、人元、物元”等表示未知数
等式
方程
回顾方程
1+2=3
5=7-2
3+b=2b+1
4+x=7
0.7x=1400
2x-2=6
1、像这种用等号“=”来表示相等关系的式子,叫 。
2、像这样含有未知数的等式叫做 。
判断方程的两个关键要素:
①有未知数 ②是等式
请大家观察左边的这些式子,看看它们有什么共同的特征?
判断下列各式哪些是方程?
×
√
×
×
√
①5x +3y-6x =37( ) ②4x -7( )
③5x ≥ 3 ( ) ④ 6x ?+x -2=0 ( )
⑤1+2=3 ( ) ⑥ ( )
√
回顾方程
合作交流,探索新知
问题:一辆客车和一辆卡车同时从A地出发,沿同一条公路同方向行驶,客车的行驶速度是70km/h,卡车的行驶是60km/h,客车比卡车早1h经过B地。A、B两地的路程是多少?
你会用算术方法解决这个问题吗?列算式试试。
(1)客车比卡车早1h经过B地,说明当客车到达B地时,两车相差1h的卡车行驶路程。
(2)客车每小时比卡车多走( )km
(3)客车走了( )小时
10
6
60÷(70-60)×70=420(km)
x
x
思考
算术方法: 列出的算式表示解题的计算过程,其中只能用已知数.对于较复杂的问题,列算式比较困难.
列方程(代数方法): 方程是根据题中的等量关系列出的等式.其中既含已知数,又含未知数.使问题的已知量与未知量之间的关系很容易表示,解决问题就比较方便.
所以,从算术到方程是数学的进步
小试牛刀
例1.根据下列问题,设未知数并列方程(1)用一根长24cm的铁丝围成一个正方形,正方形的边长是多少cm?
列方程: 4 =24
解:如设正方形的边长为 cm,
x
x
一显身手:
解:设x月后这台计算机的使用时间达到 2450 小时。
根据题意得:1700 + 150x = 2450
(2)一台计算机已使用1700小时,预计每月再使用150小时,经过多少月这台计算机的使用时间达到规定的检修时间2450小时?
已用的时间+还可用时间150x小时=规定的检测时间2450小时.
相等关系:
我探究我发现
(3)某校女生占全体学生数的52%,比男生多80人,这个学校有多少学生?
列方程 0.52x-(1-0.52)x=80
解:设这个学校有X人,那么女生人数( ) ,
男生人数为( )。
等量关系:女生比男生多80人。
0.52x
(1-0.52)x
4x=24,
1700+150x=2450,
0.52x-(1-0.52)x=80
③等号两边都是整式;
①都只含有一个(一种)未知数;
②未知数的次数都是1;
④一次项系数不能为零。
下面的三个方程:
有什么共同点?
一元一次方程:
只含有一个未知数(元),未知
数的次数都是1,等号两边都是整式,这样的方程叫一元一次方程。
我探究,我发现
小试身手
注意:一元一次方程中,只含有一个未知数,且未知数的次数都是1,等号两边都是整式。
接下来,拟人情境动画:判断下列成员是否一元一次方程家族成员?能否进入家庭聚会之门?若不行,请说明理由。
第一组① 5x = 0 ②1+3x ③ y2 = 4+y
④ 3m+2 = 1-n ⑤ x = 6 ⑥ +2x=5
第二组:若2x b+1 = 5, (a-1)x2+x = 3也想参加聚会,a、b满足什么条件?
归纳:书P79
像之前那样在解答实际问题时,为了方便思考,利用方程的方法去解答,这就是方程的思想。
总结反思:
1.设:恰当的设出未知数,用字母X表示问题中的未知量
3.列:利用实际问题中的相等关系列出方程
2.找:寻找实际问题中的相等关系
关键
列出一元一次方程的一般步骤:
一种方法——列方程解决实际问题的方法;
两个概念——方程、一元一次方程。
1、通过本节的学习你有什么收获?
2、在这部分学习中,你还有什么困难?
作 业
1、必做题:P83页习题3.1 第一题
2、选做题:天平的两个盘A、B内分别盛有51g、45g盐,设应该从盘A内拿出多少g盐放到盘B内,才能使两者所盛盐的质量相等?
